Johnson-Neyman图通常简称为J-N图, 主要用于可视化调节效应。
调节效应可视化的最简单方法是“选点法”(Rogosa,1980)或“简单斜率”(Aiken 和 West,1991)方法,最简单的方法是选择调节变量的两个取值(“均值+标准差”和“均值-标准差”),并通过假设检验或构建置信区间来研究在这两个取值下, 绘制两条线来表示自变量与因变量的关系, 线的斜率就是简单斜率。尽管易于执行,但该方法的缺点很明显, 很多学生都问我, 为什么选择这两个取值(“均值+标准差”和“均值-标准差”), 我其实没有很好的理由说服他们, 他们就是任意的选点。如果你把这两个选点的范围扩大, 比如使用两倍的标准差, 那么很可能扩大斜率的差异, 也就是说, 扩大调节变量的范围, 可以让本来不显著的调节效应变成显著。
Johnson-Neyman技术概括
调节变量简称M, 自变量简称X,因变量简称Y, 当调节变量M是连续的时,更合理的方法是 JN 方法(Johnson 和 Neyman,1936)。 JN 技术不是测试固定 M 值情况下简单斜率的显著性,而是考虑所有M的取值, 求得一个M的范围, 在该范围内, X对Y的影响是显著的(Bauer 和 Curran,2005)。JN图(J-N图)通过置信带图可以轻松了解调节变量的取值范围下,X对Y的影响是显着的。 “选点法”可以被视为局部“聚光灯”方法,而 JN 技术可以被视为全局“泛光”方法(Spiller 等,2013)。
J-N图已有方案的缺陷
如果你会编程(例如,R 或 SAS),则可以实现 JN 图(很多R包可以制作JN图)。但是我们的目标是让那些没有任何编程经验的人更广泛地使用 JN 技术。此外,我们的解决方案(一个Excel工作簿)是直接而简单的,因为用户输入数据和创建漂亮的图形之间只有一个步骤。确实存在一些用于实施 JN 的现成解决方案,但它们存在以下几个缺点之一。
- 最著名的是 SAS 和 SPSS 的 PROCESS 插件(Hayes,2013b)。这有一些问题, 一些研究人员无法使用 SAS 或 SPSS,因为这些软件的价格昂贵。
- SPSS绘图很丑,JN 图形输出需要“大量编辑”(Hayes,2013b,第 242 页)。
- 可以肯定的是,有免费的解决方案,但它们至少存在以下缺点之一:图形质量差,流程不够精简,需要用户事先完成线性回归,然后才能进行JN分析
技术细节
这部分介绍了JN方法的一些数学原理, 但是你可以不关心, 看不懂这部分不影响你使用我们提供的Excel工具。
最简单的调节效应模型可以用下面的公式表示:
Y代表因变量, X是自变量, M是调节变量。
因为X是我们关心的自变量, 我们可以将公式转换为X的函数:
这个函数形式是强调了M可以是一个取值, X是真正的变量。不如我们用更简单的替换来表达:
这样我们可以得到一个更简介的公式, 这是一个简单的一般线性回归模型, X的斜率(回归系数)就是ω1:
根据已有的回归方法, 我们可以推导出来回归系数ω1的标准误是:
因为知道了标准误, 就可以进行t检验, t值是:
根据这个公式, 我们可以求得M取什么值的范围可以让t值保持在显著水平(95%的置信区间)。
Excel绘制JN图
我们制作了一个Excel模板可以方便的绘制JN图,做法很简单。
首先可以被编辑的区域是深色的,如图:
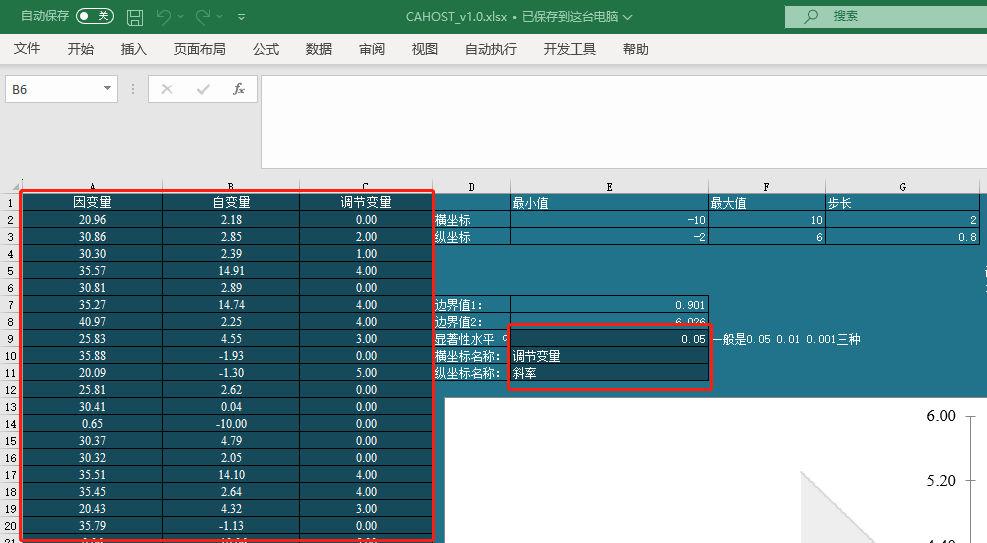
你需要做的就是输入自变量、因变量、调节变量的数据, 然后设置显著性水平(大部分人设置为0.05),
最后设置横坐标和纵坐标名称。
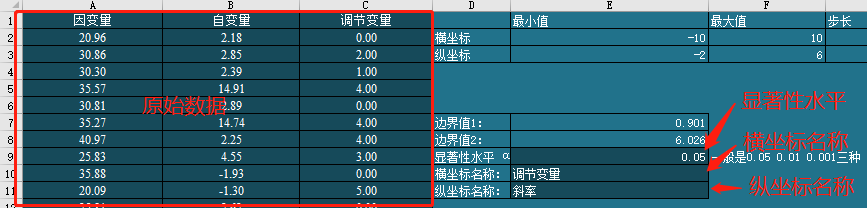
到这里,你可能看到的图是混乱的,因为Excel不能合理的设置纵坐标的数值,
至少不能得到我们想要的样子, 那么我们需要手动设置坐标轴。
- 首先,我们注意表格中输出了坐标轴的一些建议参数,你可以参考

然后双击横坐标轴,这步操作就是为了打开图标设计侧边框,如果你点击的准确,就应当看到横坐标轴是选中状态,如图所示:
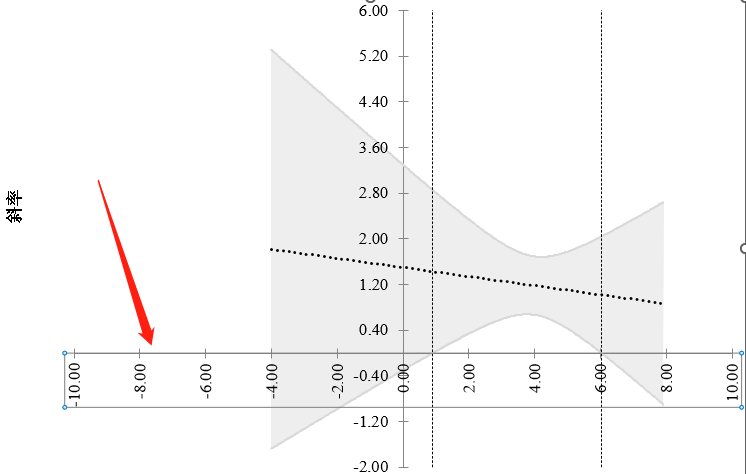
在右侧边出现如图所示的设计窗口:
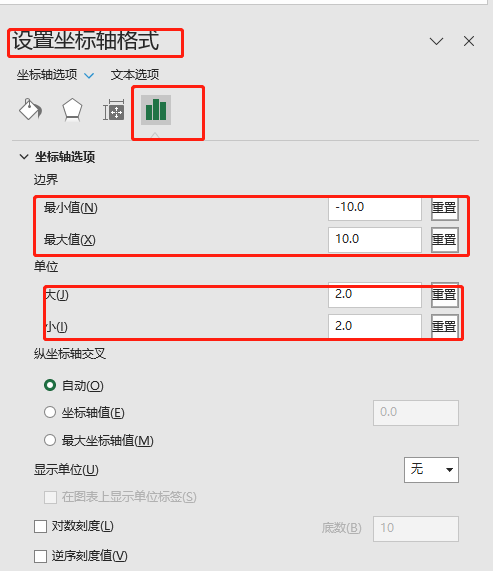
我们已经给了你坐标轴的建议取值范围,他们与设计窗口的对应关系可以看下图:
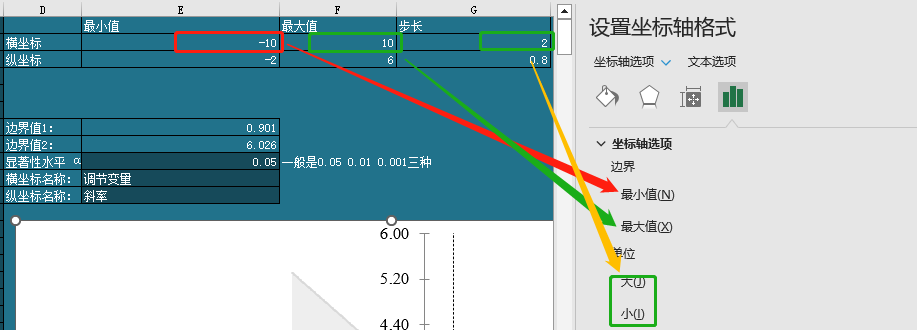
你注意我们目前选中的是横坐标, 所以你设置的是横坐标, 当你设置完横坐标, 再选择纵坐标进行设置。
到此你的图就画好了, 如果图文看起来麻烦, 可以看下面的视频教程。
Johnson-Neyman图Excel绘制视频教程
Johnson-Neyman图如何解读
我们从网络上找到了几种JN图的类型, 我们可以分别写一下结论:
案例1: 当调节变量M的取值小于-1.7的时候,斜率是显著的;

案例2: 当调节变量M的取值大于1.5的时候,斜率是显著的;

案例3: 当调节变量在1到6之间的时候,斜率是显著的;

案例4: 当调节变量小于0.1或者大于4.8的时候,斜率是显著的;

案例5: 调节变量的所有取值范围下,斜率都是显著的;

案例6: 调节变量的所有取值范围下, 斜率都是不显著的;

工具从哪里下载
说明: 这个工具制作不易,所以我们设置了密码保护,你看不到计算过程,我们不会公布密码;
另外会收取几块钱小额赞助, 这样我们才能持续贡献有价值的统计工具。