这是一个表格卡方检验计算器. 不论你找的是4格表还是6格表多格表都是一样的. 下面介绍一下卡方检验的原理, 以及何时对卡方进行校正.
卡方分布
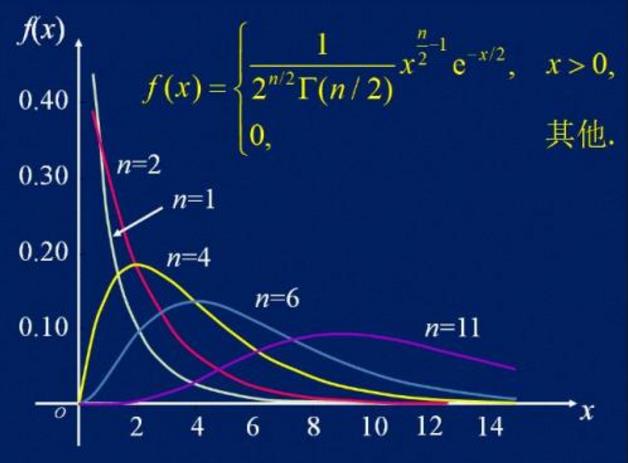
以上是卡方分布的图像, 图中n就是卡方分布的参数–自由度(DF). 自由度决定了卡方分布的图像形状. 自由度的计算方法如下公式, 其中Row代表表格的行数, Column代表表格的列数. 依次四格表的卡方自由度是1.
\[ DF = (Row-1) \times (Column - 1) \]
期望值计算公式
每个单元格的期望值就是在虚无假设成立的情况下, 期望得到的计数数据. 可以通过如下公式计算. 其中, \( M_r \)代表单元格所在行的所有单元格观察数之和; \( M_c \)代表单元格所在列的所有单元格观察数之和. 观察值就是每个单元格的计数数据.
\[ E= {M_r \times M_c \over Total} \]
卡方计算
如下是卡方的计算公式, 下标r代表行数, 下标c代表列数. O代表Observe, 即观察数. E代表Expect, 即期望数.
\[ \chi^2= \Sigma_r \Sigma_c {O_{rc}^2-E_{rc}^2 \over E_rc} \]
何时使用Yates校正卡方值
在单元格中的期望值有20%的期望值低于5. Yates实际降低了卡方值, 使得显著的可能性降低.
\[ Yates's \chi^2= \Sigma_r \Sigma_c {|O_{rc}^2-E_{rc}^2| -0.5 \over E_rc} \]
如何使用下面的卡方计算器
下面的表格, 每一行代表一种实验结果, 每一列代表一组人群. 比如, 现在有男女两种人群, 有有效和无效两种实验结果, 那么假如男生有30个有效, 40个无效, 女生有20个有效, 15个无效. 我们填写到下面的数据布局就是:
| —- |男|女|
|有效|30|20|
|无效|40|15|
只要你填写的数据正确, 下面就会自动显示计算结果, 里面有卡方值和Yates卡方值, 和他们的P值, 注意, P值是卡方值到0之间的积分, 因此, 只有大于95%才认为是显著.
