:纯随机序列: 平稳序列值之间没有任何相关性的序称为纯随机序列,这意味着该序列过去的行为对将来的发展没有丝毫影响. 从统计分析的角度而言, 纯随机序列没有任何分析价值. 纯随机序列也称为白噪声序列.
在进行时间序列建模之前, 我们最好先对序列进行纯随机性检验, 防止做无用功. 这篇文章主要内容是用python进行纯随机检验.
数据来源
本教程的数据都来自于王燕的<应用时间序列分析>随书数据, 你可以在我的github上下载.
时序图
通常拿到一个序列数据, 我们第一件事情就是绘制它的时序图来观察一下数据的基本走势. 用时序图来观察数据随时间的变化, 直观易懂, 但是具有主观性.
我们先来用一个随机数据, 观察它的时序图:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| import pandas as pd
import os
import random
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
DATA_DIR='../data/sample/'
random.seed(10)
def random_sequence_chart():
dpath = os.path.join(DATA_DIR, '附录1.1.xls')
data=pd.read_excel(dpath)
for i in range(data.shape[0]):
data.iloc[i, 1]=random.randint(20, 200)
print(data)
fig, ax = plt.subplots()
ax.plot(data['年份'], data['黑子数'])
ax.set(xlabel='年份', ylabel='黑子数', title='随机生成的黑子数')
plt.savefig('../imgs/random-sunspots.png')
plt.show()
random_sequence_chart()
|
你会看到如下所示的时序图, 你大概就能看出这是一个完全随机的序列图.
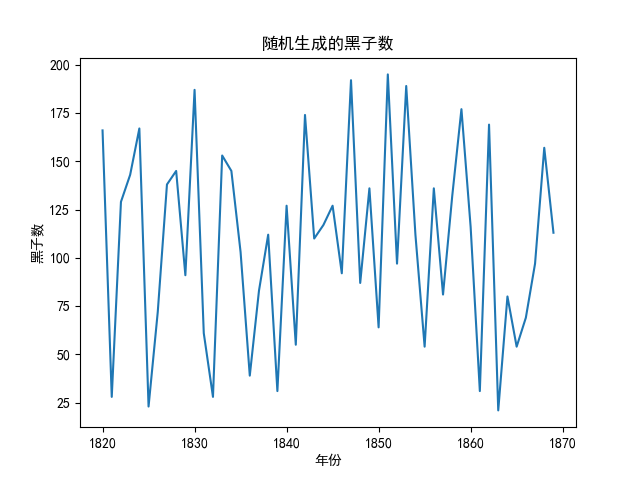
但是, 对比一下真实的数据, 我们把历年的真实太阳黑子数绘制在时序图上:
1
2
3
4
5
6
7
8
9
10
| def sequence_chart():
dpath = os.path.join(DATA_DIR, '附录1.1.xls')
data=pd.read_excel(dpath)
fig, ax = plt.subplots()
ax.plot(data['年份'], data['黑子数'])
ax.set(xlabel='年份', ylabel='黑子数', title='黑子数')
plt.savefig('../imgs/sunspots.png')
plt.show()
sequence_chart()
|
生成如下图:
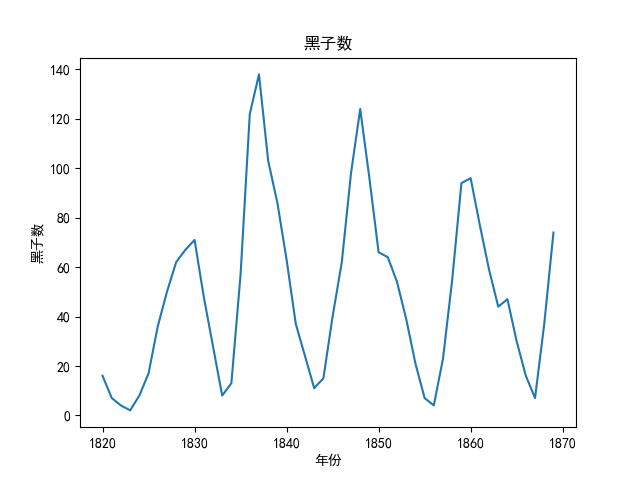
自相关图
自相关图就是将n步自相关系数绘制成一个折线图. 注意统计学意义上的aotucorrelation和信号处理中用到的autocorrelation是不同的. 如果你用matplotlib.pyplot.acorr来绘制自相关图, 得到的是信号处理中常用的算法. 而如果使用pandas中的pandas.plotting.autocorrelation_plot得到的就是n步的皮尔逊相关.
下面我们对比一下完全随机序列和非随机序列的自相关图的差异:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| def autocorr():
from pandas.plotting import autocorrelation_plot
dpath = os.path.join(DATA_DIR, '附录1.1.xls')
data=pd.read_excel(dpath)
fig, axes=plt.subplots(nrows=2, ncols=1)
autocorrelation_plot(data['黑子数'], ax=axes[0])
axes[0].set_title('真实黑子数')
x=[random.randint(1, 200) for i in range(data.shape[0])]
autocorrelation_plot(x, ax=axes[1])
axes[1].set_title('随机黑子数')
plt.savefig('../imgs/autocorr.png')
plt.show()
if __name__=='__main__':
autocorr()
|
可以生成如图所示的自相关图:
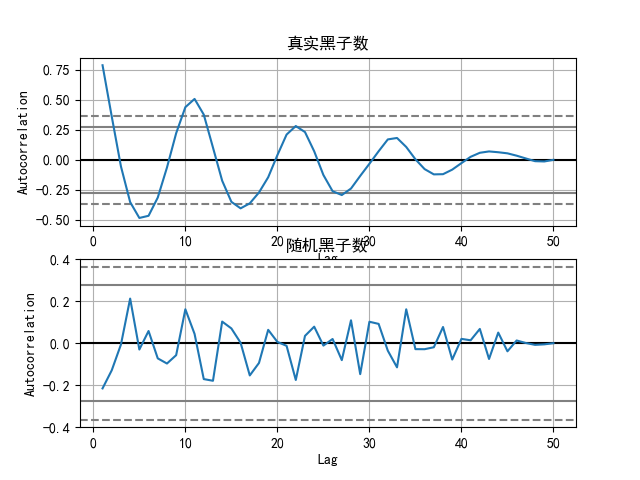
从图中可以看出, 如果数据呈周期性变化, 自相关图就会呈周期性变化. 而完全随机的序列数据是没有规律的, 并且绝大部分相关值都集中在0附近.
假设检验原理
假设检验的原理来自于<应用时间序列分析(王燕)>:



Q和LB统计量的计算
下面我们通过python代码来实现对Q统计量的检验. 计算Q统计量和LB统计量都是用python中statsmodels模块中的acorr_ljungbox方法. 默认情况下, acorr_ljungbox只计算LB统计量, 只有当参数boxpierce=True时, 才会输出Q统计量.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| def boxpierce_test():
'''计算box pierce 和 box ljung统计量'''
from statsmodels.sandbox.stats.diagnostic import acorr_ljungbox
dpath = os.path.join(DATA_DIR, '附录1.1.xls')
data=pd.read_excel(dpath)
x=data['黑子数']
qljungbox, pval, qboxpierce, pvalbp=acorr_ljungbox(x, boxpierce=True)
for i in range(len(pval)):
print('真实数据:qljungbox, pval, qboxpierce, pvalbp:',qljungbox[i], pval[i], qboxpierce[i], pvalbp[i])
fig, axes = plt.subplots(2,2)
axes[0,0].plot(qljungbox, label='qljungbox');axes[0,0].set_ylabel('真实-Q')
axes[0,0].plot(qboxpierce, label='qboxpierce')
axes[0,1].plot(pval, label='pval');axes[0,1].set_ylabel('P')
axes[0,1].plot(pvalbp, label='pvalbp')
x=[random.randint(1, 200) for i in range(data.shape[0])]
qljungbox, pval, qboxpierce, pvalbp=acorr_ljungbox(x, boxpierce=True)
axes[1,0].plot(qljungbox, label='qljungbox');axes[1,0].set_ylabel('随机-Q')
axes[1,0].plot(qboxpierce, label='qboxpierce')
axes[1,1].plot(pval, label='pval');axes[1,1].set_ylabel('P')
axes[1,1].plot(pvalbp, label='pvalbp')
axes[0,0].legend()
axes[0,1].legend()
axes[1,0].legend()
axes[1,1].legend()
plt.savefig('../imgs/boxpierce_test.png')
plt.show()
print('随机数据:qljungbox, pval, qboxpierce, pvalbp:',qljungbox, pval, qboxpierce, pvalbp)
if __name__=='__main__':
boxpierce_test()
|
输出可视化的结果是:
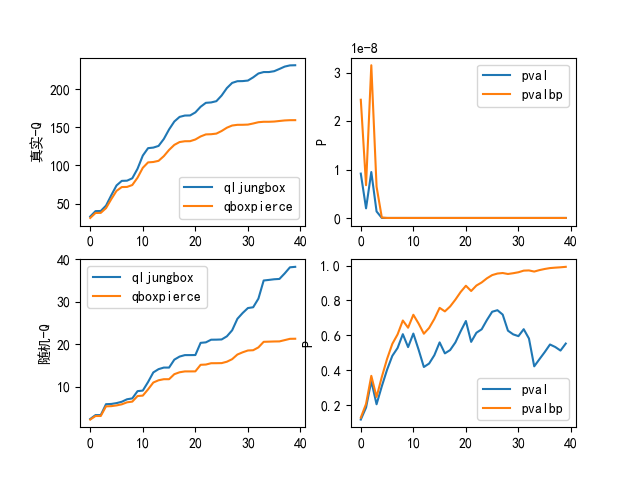
从图中, 我们可以看出随机时间序列数据的p值基本都在0.5以上, 也就是说不能推翻虚无假设, 虚无假设可能是正确的, 也就是说这是一个白噪音序列.
而真实数据的p值都在0.05以下, 说明虚无假设的成立时小概率事件, 所以虚无假设更大的可能是不成立的, 也就是说这个不是一个白噪音序列.







