单因素方差分析指的是自变量只有一个的方差分析,实验的设计一般是将被试随机分配到不同的自变量水平,这样不同的分组就代表着不同的自变量水平,值得注意的是,自变量虽然只有一个,但是因变量可以有两个甚至更多。下面是具体的方法。
工具/原料
-
spss20.0
方法/步骤 -
在spss中打开你要处理的数据,在菜单栏上执行:analyse-compare means–one-way anova,打开单因素方差分析对话框
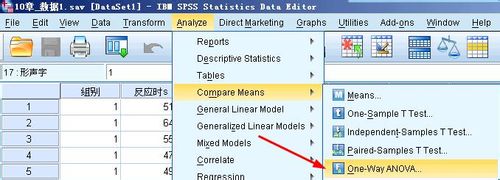
- 在这个对话框中,将因变量放到dependent list中,将自变量放到factor中,这个研究中有两个因变量,所以把两个因变量都放到上面的列表里
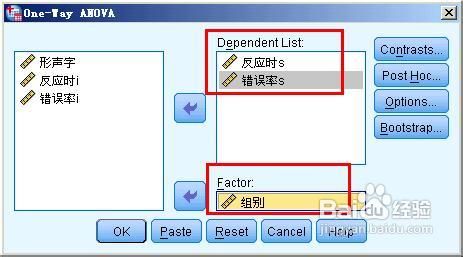
- 点击post hoc,打开一个对话框,设置事后检验的方法
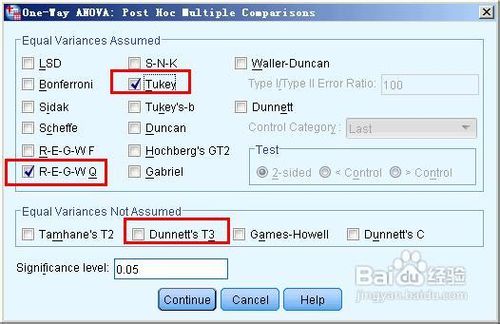
- 在这个对话框中,我们在上面的方差齐性的方法中选择tukey和REGWQ,在方差不齐性的方法中选择dunnetts,点击continue继续
- 回到了anova的对话框,点击options按钮,设置要输出的基本结果
- 这里选择描述统计结果和方差齐性检验,点击continue按钮

- 点击ok按钮,开始处理数据

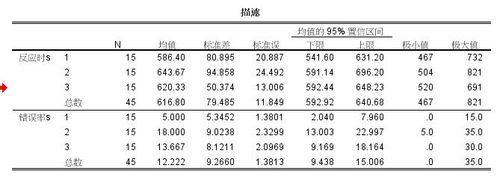
- 我们看到的结果中,第一个输出的表格就是描述统计,从这个表格里我们可以看到均值和标准差,在研究报告中,通常要报告这两个参数
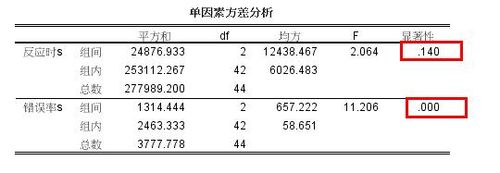
- 接着看方差齐性检验,方差不齐性的话是不能够用方差齐性的方法来检验的,还好,这里显示,显著性都没有达到最小值0.05,所以是不显著的,这证明方差是齐性的

- 接着看单因素方差分析表,反应时sig值不显著,而错误率达到了显著的水平,这说明实验处理对错误率产生了影响,但是对反应时没有影响
-
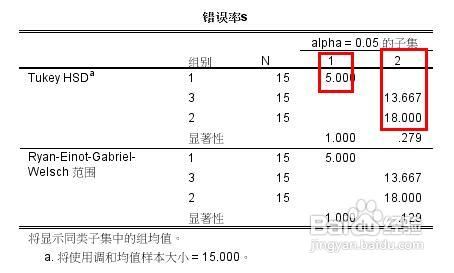
接着看事后检验,因为反应时是没有显著差异的,所以就不必再看反应时的事后检验,直接看错误率的事后检验,从图中标注的红色方框可以看到,第一组和二三组都有显著的差异,而第二组和第三组没有显著差异。关于dunnet方法,它适合在方差不齐性的时候使用,因为方差齐性,不必去看这个方法的检验结果了

-
最后我们看这个表格,这里有两个检验方法都是在方差齐性的时候使用的,我们从红色方框可以看出第一组分为一组,第二三组分为一组,它的意思是上面的结果是一致的。
转载请注明来自DataScience.
邮箱: 675495787@qq.com