方差 - 是什么?
作者:Ruben Geert van den Berg,归属于 Statistics A-Z 和 ANOVA
方差 (Variance) 是一个数值,它表示一组数字彼此之间的离散程度。方差与标准差的平方相同,因此表达的是“相同的事情”(但程度更强)。
方差 - 示例
一项研究让100人执行一个简单的速度任务,共进行80次试验。对于每位参与者,记录80个反应时间(以秒为单位)。部分数据如下所示。

在类似这样的研究中,我们通常会看到,随着人们更频繁地执行速度任务,他们会变得更快。也就是说,平均反应时间往往会随着试验次数的增加而减少。 此外,反应时间在不同人之间通常会 变化 较小,因为他们更频繁地执行任务。从技术上讲,我们说方差随着试验次数的增加而减少。下表说明了试验1、4、7和10的情况。
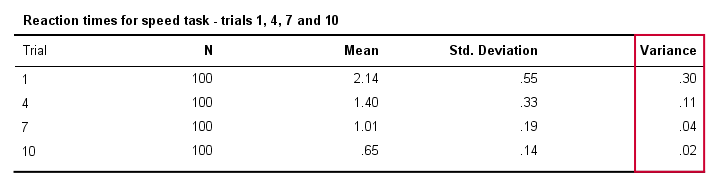
方差与直方图
可视化上表数据的绝佳方法是为每次试验绘制一个直方图。如下图所示,参与者随着试验的进行变得更快;从试验1到试验10,直方图的条形向左移动,接近0秒。
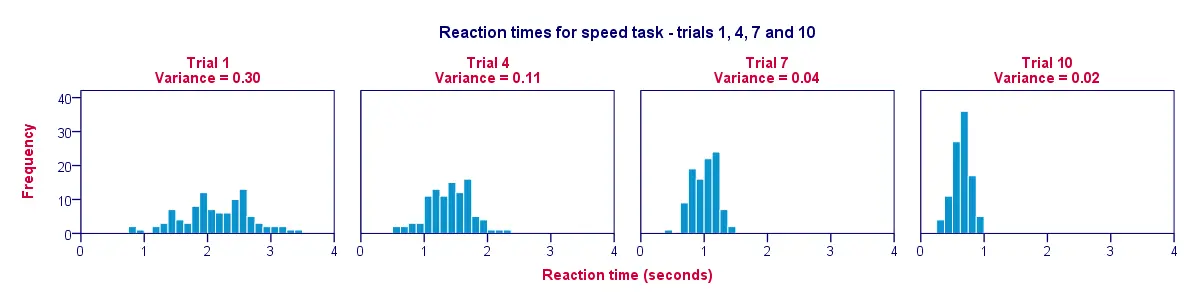
第二个发现是,随着我们从试验1移动到试验10,直方图变得更窄(因此更高);这说明随着实验的进行,参与者之间的反应时间变化越来越小。方差随着试验次数的增加而减少。
方差 - 总体公式
计算方差的一个基本公式是
\[S^2 = \frac{\sum(X - \overline{X})^2}{n}\]
我们建议您尝试理解这个公式的作用,因为这有助于理解 ANOVA(= 方差分析)。因此,我们将在少量数据上演示它。
方差 - Google表格 (GoogleSheets)
为了简单起见,我们将数据缩减为前5位参与者的第一次试验。这5个反应时间以及手动计算的方差位于 此Google表格 中。
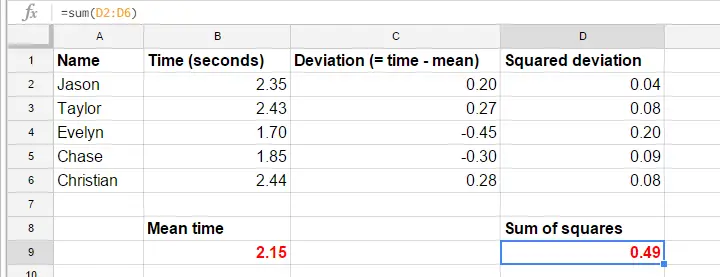
方差 - 计算步骤
Google表格中的公式精确地显示了如何计算方差。基本步骤是:
- 计算平均值 (mean) 反应时间 (2.15);
- 计算离差 (deviation scores) (反应时间减去平均反应时间);
- 计算平方离差 (squared deviation) ;
- 将平方离差相加。结果 (0.49) 是平方和 (sum of squares) ,这是 ANOVA 的主要组成部分;
- 将平方和除以 (divide) 观察次数(5个反应时间)。
或者,通过在某个单元格中键入=VARP(B2:B6)来计算方差(B2:B6是包含我们5个反应时间的单元格)。 VARP 是 “variance population” 的缩写。 OpenOffice 和 MS Excel 包含类似的公式。
方差 - 样本公式
与标准差类似,如果我们的数据是来自更大总体的简单随机样本,则上述公式将系统地低估总体方差。在这种情况下,我们将使用略有不同的公式:
\[S^2 = \frac{\sum(X_i - \overline{X})^2}{n - 1}\]
因此,使用哪个公式取决于我们的数据:它们是否包含我们想要调查的整个总体,或者它们只是来自该总体的样本? 由于我们的100名参与者显然是一个样本,我们将使用样本公式。在 Google表格 中,在某个单元格中键入 =VAR(B2:B6) 将返回样本方差。
SPSS 中的方差
据我们所知, SPSS 完全没有总体方差的公式,我们认为这是一个严重的缺陷。相反,SPSS 始终使用样本公式。这适用于主体间方差(在本教程中讨论)以及主体内方差。相关输出如下所示。

关于此输出表,另请注意,方差确实是标准差的平方(四舍五入除外)。
关于方差,就是这些了。我们希望本教程对您理解方差有所帮助。