SPSS 单因素方差分析教程
作者：Ruben Geert van den Berg，发表于 ANOVA 专栏下。
想要了解一些基础知识，请参考 ANOVA - 是什么？
- 单因素方差分析 - 零假设
- 方差分析的假设
- SPSS 方差分析流程图
- SPSS 单因素方差分析对话框
- SPSS 方差分析输出结果
- 方差分析 - APA 报告指南
方差分析示例 - 肥料对植物的影响
一位农民想知道哪种肥料最适合他的欧芹。因此，他在不同的植物上尝试不同的肥料，并在 6 周后称重这些植物。数据（部分如下所示）位于 parsley.sav 文件中。
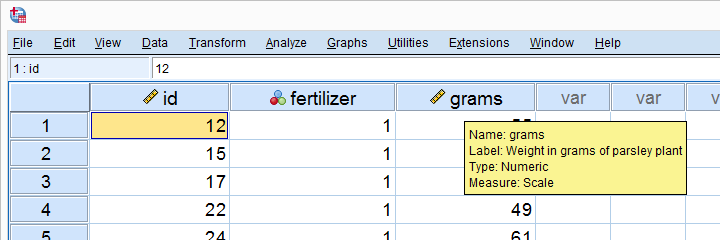
快速数据检查 - 分割直方图
在 SPSS 中打开我们的数据后，让我们首先看看它们的基本外观。一种快速的方法是分别检查每种肥料的重量直方图。下面的截图将指导您完成。
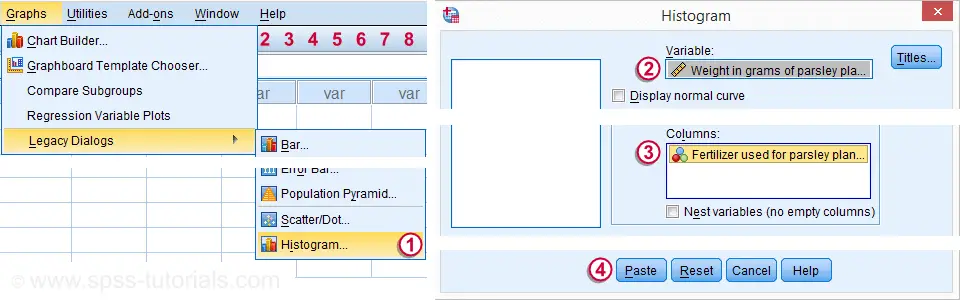
按照这些步骤操作后，单击“粘贴（P aste）”将生成下面的 语法（syntax） 。让我们运行它。
*** 运行分割直方图。
**
GRAPH
/HISTOGRAM=grams
/PANEL COLVAR=fertilizer COLOP=CROSS.结果
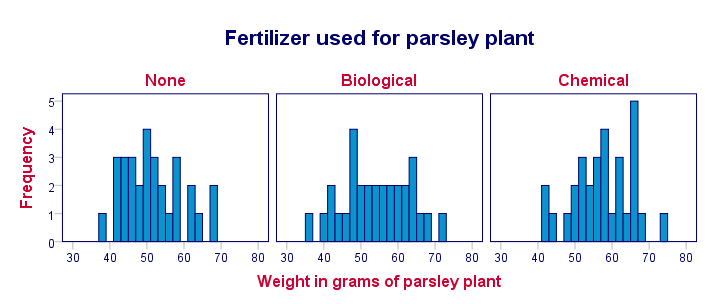
重要的是，这些分布看起来是合理的，我们没有看到任何异常值：我们的数据从一开始看起来是正确的 - 在真实世界的数据中并不总是这样！
结论：绝大多数重量在 40 到 65 克之间，并且看起来相当符合 正态分布（normally distributed）。
检查样本量和均值
肥料究竟如何影响植物？让我们分别比较一下不同肥料的一些描述性统计数据。最快的方法是使用 MEANS 命令，我们可以从“分析（A nalyze）”
“比较均值（C ompare Means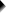）” “均值（M eans）”中粘贴，但直接输入语法可能同样容易。
*** grams (克) 按 fertilizer (肥料) 的基本描述性统计表。
**
means grams by fertilizer
/cells count mean stddev.结果
- 每种肥料的样本量均为 n = 30。
- 其次，化肥导致了最高的平均重量，接近 57 克。“None”表现最差，约为 51 克，而“Biological”介于两者之间。
- “Biological”的标准差略高于其他条件，但差异非常小。
现在，这张表告诉我们很多关于植物 样本 的信息。但是我们的 样本 均值对 总体 均值有什么说明呢？我们能对肥料对 所有（未来）植物的影响说些什么呢？我们将尝试通过驳斥所有肥料表现相同的说法来做到这一点：我们的零假设。
单因素方差分析 - 零假设
方差分析的零假设是： 所有总体均值都相等。 如果这是真的，那么我们的样本均值无论如何可能都会略有不同。但是，非常 不同的样本均值与总体均值相等的假设相矛盾。在这种情况下，我们可以得出结论，这个零假设可能根本不是真的。
方差分析基本上会告诉我们，我们的零假设在多大程度上是可信的。但是，它需要一些关于我们数据的假设。
方差分析的假设
- 独立观察（independent observations）：数据中的每条记录必须是一个不同的、独立的实体。准确地说，假设是“独立同分布的变量”，但透彻的解释超出了本教程的范围。
- 正态性（normality）：因变量在总体中呈正态分布。对于合理的样本量，例如每个 n ≥ 25，则不需要正态性。
- 方差齐性（homogeneity）：因变量的方差在每个亚总体中必须相等。仅当样本量（明显）不相等时才需要方差齐性。在这种情况下，可以使用 Levene’s 检验 来查看是否满足方差齐性。
那么如何检查我们是否满足这些假设呢？如果我们违反了这些假设该怎么办？下面的简单流程图将指导我们完成。
SPSS 方差分析流程图
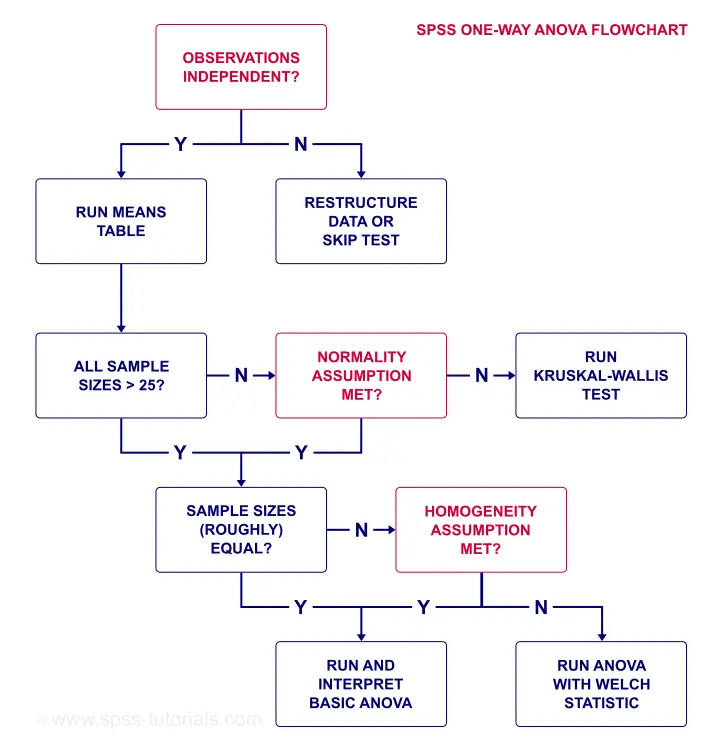
那么我们的数据呢？
- 我们的植物似乎是独立观察：每个植物都有不同的 id 值（第一个变量）。
- 我们的均值表显示每个 n ≥ 25，因此我们不需要满足正态性。
- 由于我们的样本量相等，我们也不需要方差齐性假设。
那么我们为什么要根据均值表检查我们的样本量呢？为什么我们不直接查看 fertilizer (肥料) 的频率分布呢？好吧，我们的方差分析只使用在因变量上没有 缺失值（missing values） 的个案。我们的均值表准确地显示了这些个案。
第二个原因是我们需要报告每组的均值和标准差。均值表为我们提供了我们想要的统计数据，并按照我们想要的顺序排列。
SPSS 单因素方差分析对话框
我们现在将从菜单运行一个基本的方差分析。下面的截图将指导您完成。
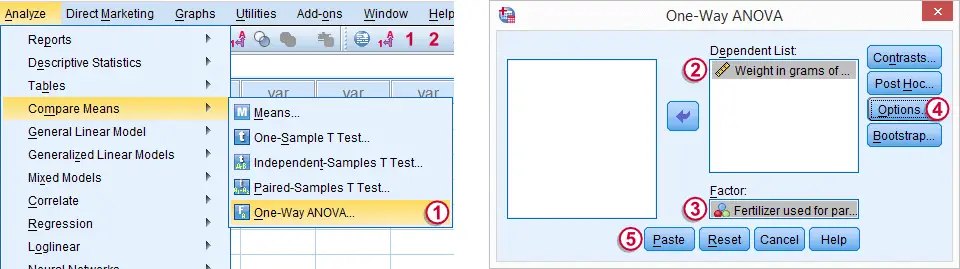
“粘贴（P aste）”按钮创建了下面的 语法（syntax）。
单因素方差分析语法
*** 基本单因素方差分析语法。
**
ONEWAY grams BY fertilizer
/MISSING ANALYSIS.SPSS 单因素方差分析输出结果
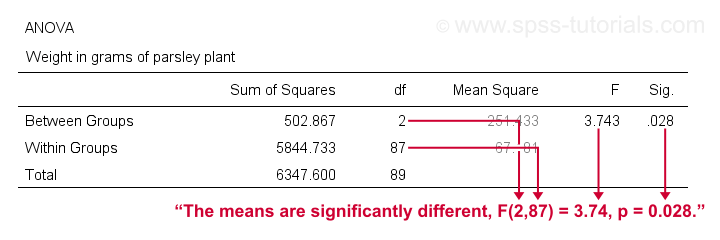
一般的经验法则是，如果“Sig.”或 p < 0.05，我们就拒绝零假设，这里的情况就是如此。因此，我们拒绝所有总体均值相等的零假设。
结论：不同的肥料表现不同。我们的平均重量之间的差异（范围从 51 克到 57 克）在 统计上是显著的（statistically significant）。
方差分析 - APA 报告指南
首先，我们将 报告我们的均值表 。关于显著性检验，APA 建议我们报告
- F 值；
- df1，分子自由度（degrees of freedom）；
- df2，分母自由度；
- p 值
像这样： “我们的三种肥料条件导致欧芹植物的平均重量不同，F(2,87) = 3.7, p = .028。”
单因素方差分析 - 下一步
对于这个例子，我们 可以 再看看两件事：
- 事后检验（Post hoc tests）：我们的方差分析结果告诉我们，并非所有总体均值都相等。但是，究竟哪个均值与其他哪个均值不同呢？这可以通过运行 事后检验 来回答。有关优秀的教程，请参考 SPSS - 带事后检验的单因素方差分析示例 。
- 效应量（Effect size）：我们得出结论，肥料会影响平均重量，但这种影响有多大？对于方差分析，常用的 效应量 度量是 偏 eta 方（partial eta squared）。遗憾的是，效应量在“单因素（One-Way）”对话框中 отсутствует.
奇怪的是，MEANS 确实 包含 eta 方，但缺少其他基本选项，例如 Levene’s 检验。要获得完整的输出，您需要从 2 个不同的命令运行两次方差分析。这确实是 SPSS 中的一个主要愚蠢之处。我就这么说了。
从 MEANS 获取带有 Eta 方的方差分析
*** 从 MEANS 获取的方差分析包含 eta 方，但不包含 Levene's 检验或功效估计。
**
means grams by fertilizer
/statistics anova.结果
好的，这就是我能想到的最基本的 SPSS 方差分析教程。我希望你觉得它有帮助。