描述性统计 - 单个度量变量

作者：Ruben Geert van den Berg，发布于 SPSS 数据分析

引言

之前的教程介绍了一些适用于类别变量和度量变量的汇总统计量。现在，我们将讨论专门适用于度量变量的一些指标。其中最重要的指标是均值（或平均值）、方差和标准差。

我们大多数人可能都熟悉均值（或平均值），但为了完整起见，我们将简要回顾一下。均值是所有值的总和除以值的数量。 我们可以用以下公式表示这个定义：

\[\overline{X} = \frac{\sum\limits_{i=1}^n X_i}{n}\]

其中：

假设我们有一个变量 X1，包含值 8, 9, 10, 11 和 12。如果我们把这些值代入公式，会发现这些值的均值是 10：

\[\overline{X} = \frac{8 + 9 + 10 + 11 +12}{5} = 10\]

方差是每个数值与均值偏差的平方的平均值。 我们可以用以下公式表示这个定义：

\[S^2 = \frac{\sum\limits_{i=1}^n(X_i - \overline{X})^2}{n}\]

方差是一种离散度 (Dispersion) 的度量；它表示数据值之间的分散程度。

让我们重新考虑变量 X1，它包含值 8, 9, 10, 11 和 12。如果我们应用该公式，我们将发现方差为 2。统计软件可能会在此处得出值 2.5。这是因为它将总和除以 (n - 1) 而不是 n。两种方法之间的差异超出了本教程的范围，但我们将在适当的时候对其进行解释。

\[S^2 = \frac{(8-10)^2 + (9-10)^2 + (...) + (12-10)^2}{5} = 2\]

现在我们有第二个变量 X2，它包含值 6, 8, 10, 12 和 14。你如何用文字描述变量 X1 和 X2 之间的差异？它们的平均值都是 10。区别在于 X2 的值相距更远；也就是说，X2 比 X1 具有更大的方差。

变量的方差反映在其直方图的形状上。在其他所有条件相同的情况下，随着方差的增加，直方图变得更宽、更矮。下图说明了实际数据的这一点。每个变量有 1,000 个观测值，平均值正好是 100。请注意，这三个直方图对其水平轴和垂直轴使用相同的比例。

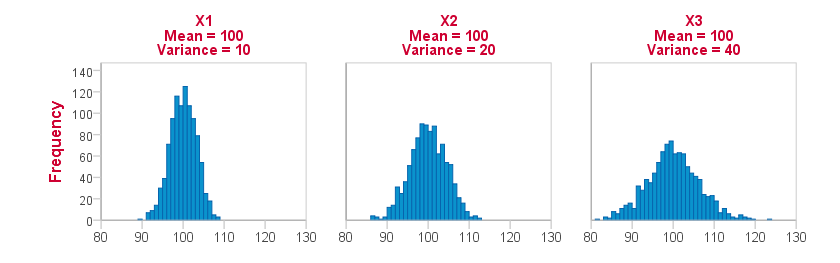相同均值，不同方差请注意，随着方差的增加，直方图如何变得更矮、更宽。

标准差是方差的平方根。 因此，它的公式与方差的公式几乎相同：

\[S = \sqrt{\frac{\sum_{i=1}^n(X_i - \overline{X})^2}{n}}\]

就像方差一样，标准差是一种离散度 (Dispersion) 的度量；它表示一组值彼此相距多远。

标准差和方差基本上表达的是同一件事，只是在不同的尺度上。那么，为什么我们不只使用一种度量来表达一组值的离散度呢？原因是对于某些情况，标准差在数学上更方便，反之亦然。