SPSS 双因素方差分析 (Two-Way ANOVA) 及交互作用教程

作者：Ruben Geert van den Berg，发表于 ANOVA 专栏

引言 & 练习数据文件

你是否觉得运行带有交互作用的双因素方差分析 (Two-Way ANOVA) 充满挑战？本教程正是为你准备的。我们将按照一个简单的流程图来进行分析，并用通俗易懂的语言解释每个步骤。阅读完本教程后，你将清楚地知道该怎么做，并且明白为什么这样做。

我们将在全文中使用 depression.sav 数据文件。下图显示了该文件在 变量视图 (Variable View) 中的样子。

SPSS 双因素方差分析 交互作用 变量视图

研究问题

简而言之，100 名患有抑郁症的参与者被分为 4 组，每组 25 人。每组都接受不同的药物治疗。4 周后，参与者填写了 BDI，即 贝克抑郁量表 (Beck’s depression inventory) 的缩写。我们的主要研究问题是：不同的药物是否导致平均 BDI 分数不同？次要问题是 BDI 分数是否与性别有关？简而言之，我们将尝试了解 4 (药物) x 2 (性别) = 8 个平均 BDI 分数。

快速检查：分数直方图

在盲目地进行统计检验之前，让我们首先看看我们的 BDI 分数是否合理。在分析任何度量变量之前，我总是首先检查它的直方图。创建直方图的最快方法是 运行以下语法 (Syntax)。

***检查直方图，看看 bdi 分数的分布是否合理。***
frequencies bdi
/format notable
/histogram.

结果

SPSS 双因素方差分析 交互作用 直方图

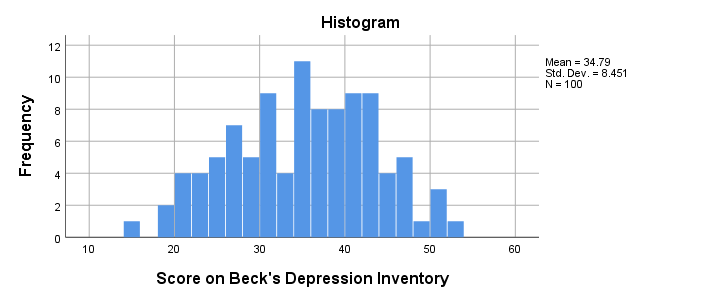
分数看起来不错。我们可能有一个只得了 15 分的异常值，但我们会将其保留在数据中。分数大致呈 正态分布 (Normally Distributed)，无需指定任何 缺失值 (Missing Values)。

方差分析 (ANOVA) 假设

当我们比较超过 2 个均值时，我们通常通过 方差分析 (ANOVA) 来进行比较。这样做需要我们的数据满足以下假设：

  • 独立观察 (Independent Observations) (或独立同分布变量)。如果每个案例都包含一个不同的人，并且参与者没有互动，通常满足此条件。
  • 同质性 (Homogeneity)：总体方差在所有子群体中都相等。如果样本量相等，则违反此假设的严重性较低。
  • 正态性 (Normality)：检验变量必须在每个子群体中呈 正态分布 (Normally Distributed)。如果样本量较大，则此假设变得不那么重要。

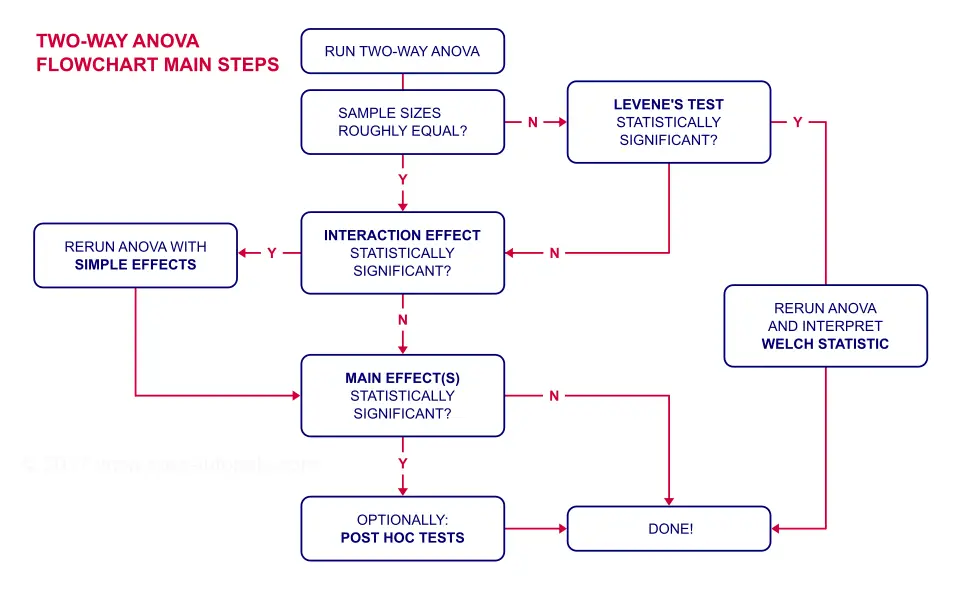
方差分析 (ANOVA) 流程图

SPSS 双因素方差分析 交互作用 显著 流程图

检查均值和样本量

我们的方差分析 (ANOVA) 流程图中的第一个问题是样本量是否大致相等。我喜欢运行均值表来检查这一点，因为无论如何我都需要在报告中使用此表。我将使用以下语法创建它。

***运行均值表并检查样本量是否大致相等。***
means bdi by gender by medicine
/cells count mean stddev.

***注意：MEANS 允许你选择你想要的统计量。***

结果

SPSS 双因素方差分析 交互作用 均值表

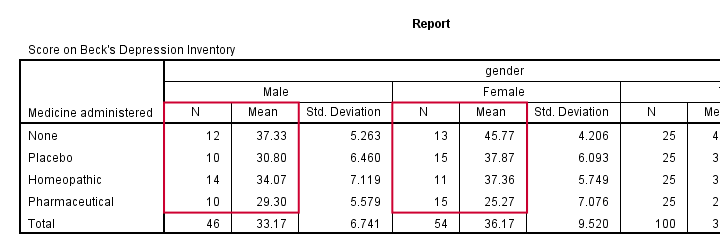
请注意，此表显示了 8 个均值（2 个性别 * 4 种药物），这是我们分析的全部内容。这 8 个均值中的每一个都基于 10 到 15 个观察值，因此样本量大致相等。这意味着我们不需要担心同质性假设。因此，我们可以跳过流程图中显示的 Levene 检验 (Levene’s Test)。

在 SPSS 中运行双因素方差分析 (Two-Way ANOVA)

我们现在将通过 分析 (Analyze) 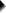SPSS 菜单箭头 一般线性模型 (General Linear Model) 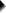SPSS 菜单箭头 单变量 (Univariate) 运行我们的双因素方差分析 (Two-Way ANOVA)。然后，我们将按照下面的屏幕截图进行操作。

SPSS 双因素方差分析 对话框 1

这将产生以下语法。让我们运行它，看看会发生什么。

***SPSS 双因素方差分析语法，从屏幕截图粘贴。***
UNIANOVA bdi BY gender medicine
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=medicine(TUKEY)
/PLOT=PROFILE(medicine*gender) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
/PRINT ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=gender medicine gender*medicine.

方差分析 (ANOVA) 输出 - 主体间效应 (Between Subjects Effects)

根据我们的流程图，我们现在应该找出交互作用是否具有 统计显著性 (Statistical Significance)。一个 -有些武断的- 惯例是，如果 “Sig.” < 0.05，则效应具有统计显著性。根据下表，我们的 2 个主效应和我们的交互作用都具有统计显著性。

SPSS 双因素方差分析 交互作用 主体间效应 1

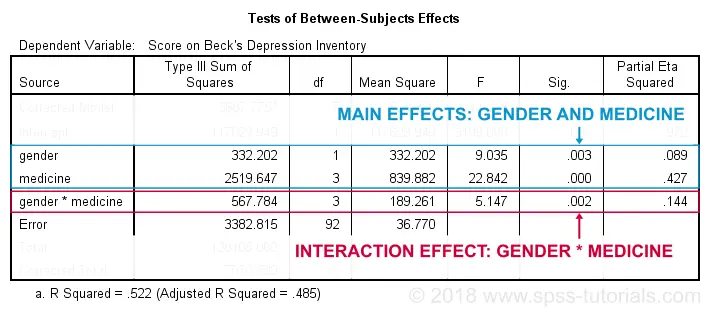
流程图表明我们现在应该使用简单效应重新运行我们的方差分析 (ANOVA)。目前，我们将忽略主效应 - 即使它们具有统计显著性。但是为什么？！如果我们理解交互作用的真正含义，这一点就会变得清楚。所以让我们检查我们的剖面图。

方差分析 (ANOVA) 输出 - 剖面图 (Profile Plots)

下图所示的剖面图基本上只显示了我们 [均值表 (Means Table)] 中显示的 8 个均值。如果你像我们刚才那样运行了方差分析 (ANOVA)，则 “估计边际均值 (Estimated Marginal Means)” 始终与我们之前看到的观察到的均值相同。有趣的是，它还显示了药物和性别如何影响这些均值。

SPSS 双因素方差分析 交互作用 剖面图

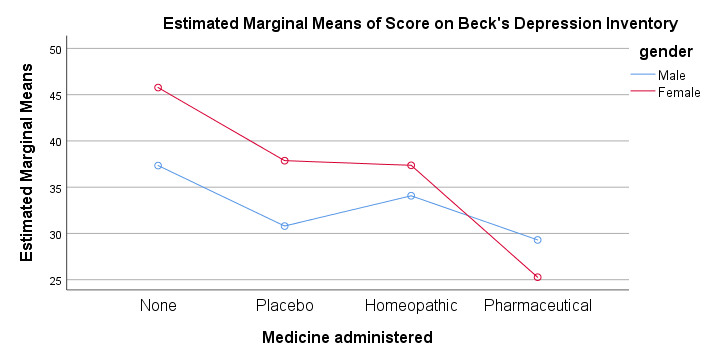
交互作用意味着一个因素的影响取决于另一个因素，并且它通过我们的剖面图中**_不_平行的线条**来显示。在本例中，药物的影响_与_性别_相互作用_。也就是说，药物对女性的影响与对男性的影响不同。粗略地说，我们看到红线（女性）从“无 (None)” 到 “药物 (Pharmaceutical)” 的下降非常陡峭，而蓝线（男性）则更加水平。由于它取决于性别，因此不存在药物的_单一_影响。这就是我们忽略药物的主要影响的原因 - 即使它具有统计显著性。这种主要影响 “将” 男性和女性的不同影响“混为一谈”，并且掩盖 - 而不是澄清 - 药物如何真正影响 BDI 分数。

交互作用？运行简单效应 (Simple Effects)。

那么我们_应该_做什么？好吧，如果药物对男性和女性的影响不同，那么我们将分别分析男性和女性参与者：我们将对每组中的药物进行 单因素方差分析 (One-Way ANOVA)。这就是我们的流程图中 “简单效应 (Simple Effects)” 的含义。

带有简单效应的方差分析 (ANOVA) - 分割文件 (Split File)

我们如何才能分别分析 2 个（或更多）案例组？好吧，SPSS 为此提供了一个很棒的解决方案，称为 分割文件 (SPLIT FILE)。它要求我们首先对案例进行排序，所以我们也会这样做。

***交互作用具有统计显著性？进行简单效应：分别对男性和女性参与者运行单因素方差分析。***
sort cases by gender.

split file separate by gender.

小提示：分割文件 (SPLIT FILE) `不会以任何方式更改你的数据。它只会影响你的输出，我们稍后会看到。你可以通过运行SPLIT FILE OFF.` 来简单地撤消它。但现在不要这样做；我们首先要运行我们的单因素方差分析 (One-Way ANOVA)，以检查我们的简单效应。

在 SPSS 中运行带有简单效应的方差分析 (ANOVA)

由于我们打开了我们的分割文件 (SPLIT FILE)，我们现在可以只运行单因素方差分析 (One-Way ANOVA)。我们将使用 分析 (Analyze) SPSS 菜单箭头 一般线性模型 (General Linear Model) SPSS 菜单箭头 单变量 (Univariate)。下面的屏幕截图将指导你完成后续步骤。

SPSS 双因素方差分析 简单效应 对话框

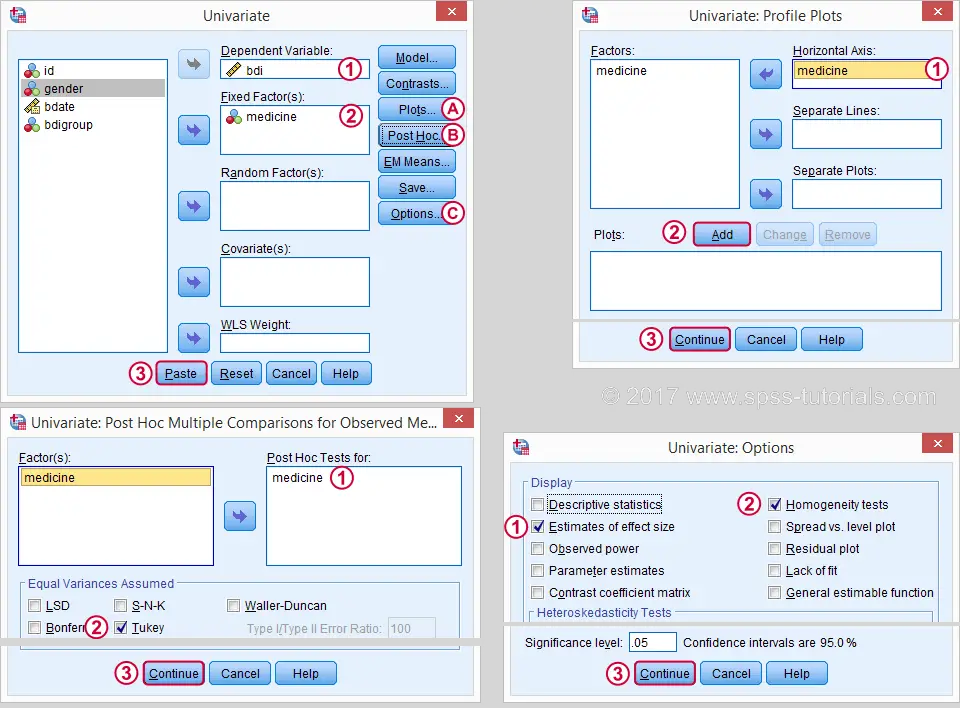
这将产生以下语法。让我们运行它。

***简单效应：通过性别 (gender) 分割文件 (SPLIT FILE)，并分别对男性和女性运行单因素方差分析 (One-Way ANOVA)。***
UNIANOVA bdi BY medicine
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=medicine(TUKEY)
/PLOT=PROFILE(medicine) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
/PRINT ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=medicine.

方差分析 (ANOVA) 输出 - 主体间效应 (Between Subjects Effects)

首先，请注意，输出窗口现在包含男性参与者的所有方差分析 (ANOVA) 结果，然后是女性的类似结果集。根据我们的流程图，我们现在应该检查主要影响。

SPSS 双因素方差分析 简单效应 输出

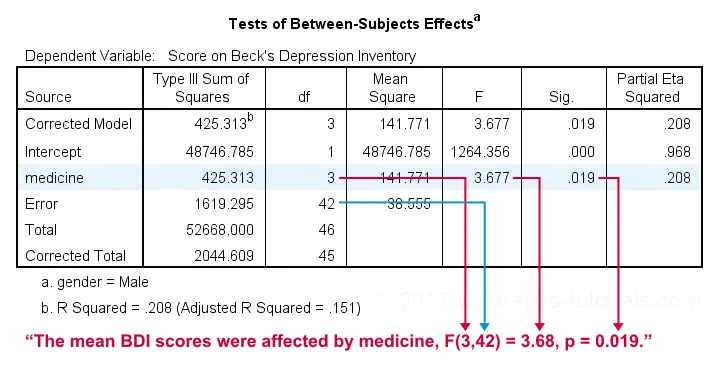
药物的影响具有统计显著性。但是，这仅仅意味着它可能不为零。但它也不是很强，如其 偏 eta 方 (Partial Eta Squared) 0.208 所示。这不应该令人感到惊讶。正如我们在剖面图中看到的那样，这 4 种药物对男性来说并没有太大的不同。

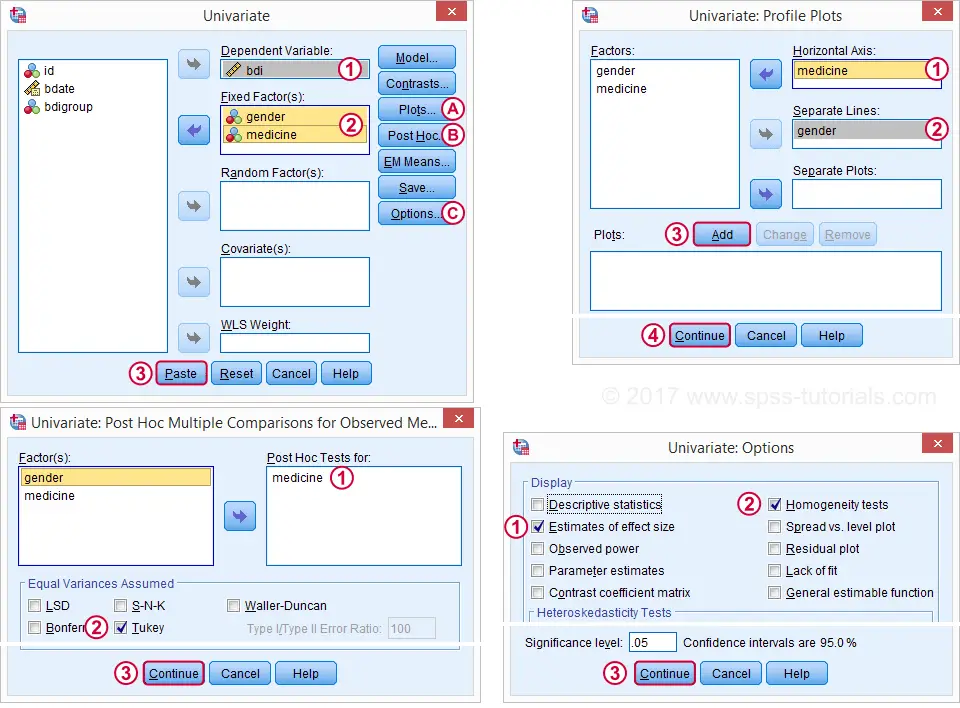
方差分析 (ANOVA) 输出 - 事后检验 (Post Hoc Tests)

我们的主要影响表明我们的 4 种药物并非都表现相似。但是哪一种（或哪些）药物与其他药物真正不同？这个问题通过我们的 事后检验 (Post Hoc Tests) 来解决，在本例中为 Tukey 的 HSD (“诚实显著差异”) 比较。

SPSS 方差分析 交互作用 显著 事后检验

此表将每种药物与其他药物进行比较（两次）。唯一产生 p < 0.05 的比较是 “无 (None)” 与 “药物 (Pharmaceutical)”。我们的 [剖面图 (Profile Plots)] 显示这些是男性参与者表现最差和表现最好的药物。所有其他药物的均值太接近，无法在统计上显着差异。

女性参与者

根据我们的流程图，我们现在已经完成了 - 至少对于男性而言。解释女性参与者的结果留给读者作为练习。但是，我想指出以下几点：

  • 我们的 [剖面图 (Profile Plots)] 显示女性的线条比男性更陡峭。
  • 药物的主要影响对女性的偏 eta 方 (Partial Eta Squared) 要高得多，为 0.63。
  • 药物的影响对女性为 p = 0.000，对男性为 p = 0.019。
  • 对于女性，所有事后比较 (Post Hoc Comparisons) 均具有统计显著性，除了 “顺势疗法 (Homeopathic)” 与 “安慰剂 (Placebo)” (p = 0.997)。

所有这些发现表明药物对女性的影响比对男性更强；BDI 分数上药物和性别之间存在显着的交互作用。这 - 再次 - 是我们需要单独分析这些组并使用简单效应重新运行我们的方差分析 (ANOVA) 的原因 - 就像我们刚才所做的那样。

最后的说明

你仍然认为运行带有交互作用的双因素方差分析 (Two-Way ANOVA) 具有挑战性吗？我希望本教程可以帮助你理解主要的思维路线。并且 - 希望如此！- 这些事情开始对你有所帮助 - 或许在第二次阅读之后。