SPSS 相关分析教程

作者：Ruben Geert van den Berg，归档于 Correlation 目录下。

目录

  • 相关性检验 - 是什么？
  • 零假设 (Null Hypothesis)
  • 假设前提 (Assumptions)
  • 在 SPSS 中进行相关性检验
  • 结果报告 (Reporting)

相关性检验 - 是什么？

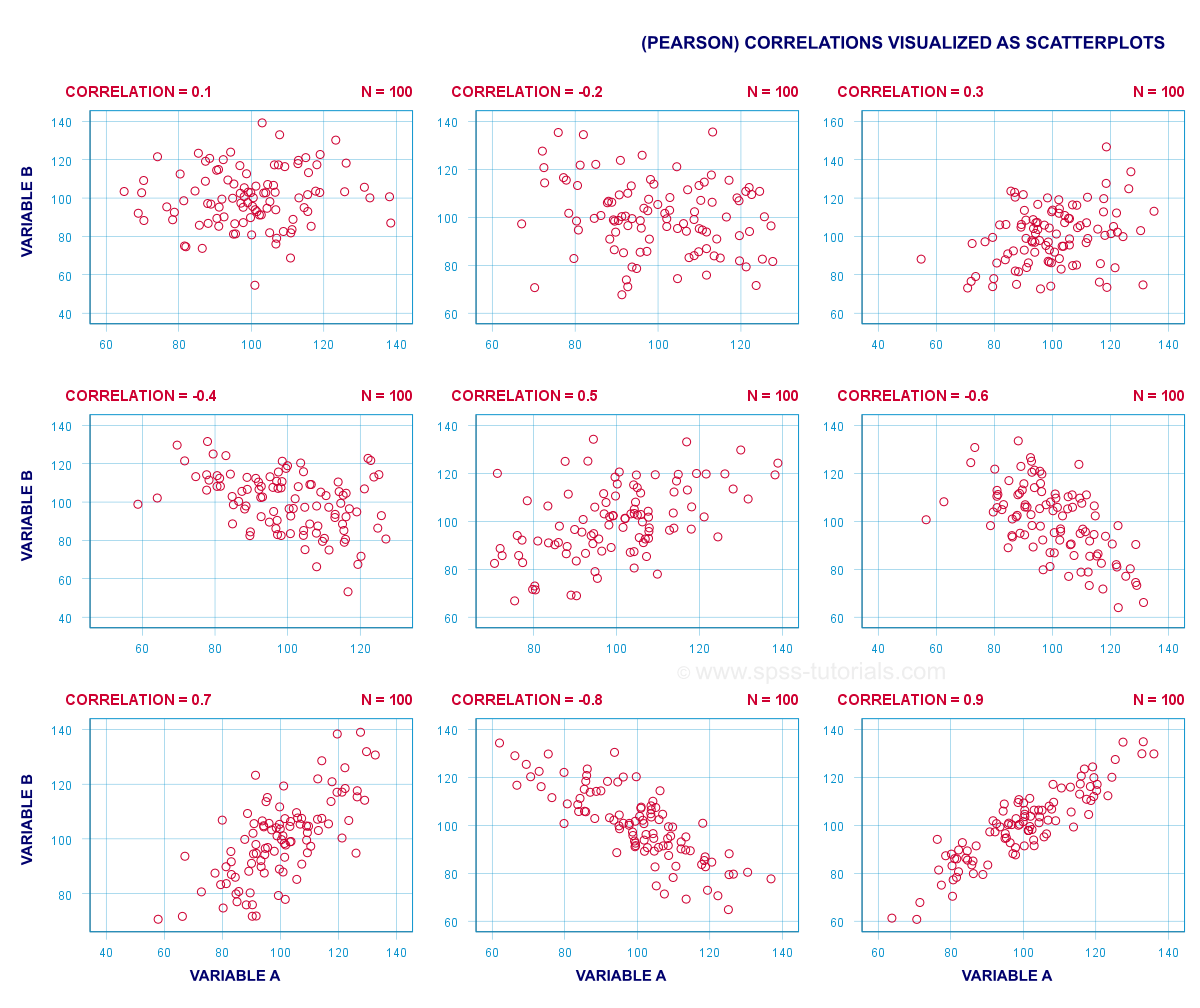
（皮尔逊）相关系数是一个介于 -1 和 +1 之间的数字，表示两个定量变量之间线性相关的程度。 理解它的最佳方式是查看一些散点图 (scatterplots)。

SPSS 相关分析散点图

简而言之：

  • 相关系数为 -1 表示完全线性递减关系：一个变量的得分_越高_，另一个变量的得分就_越低_。
  • 相关系数为 0 表示两个变量之间根本没有线性关系。 但是，可能仍然存在（很强的）非线性关系。
  • 相关系数为 1 表示完全线性递增关系：一个变量的得分越高，另一个变量的得分也越高。

零假设 (Null Hypothesis)

相关性检验（通常）检验总体相关性为零的零假设。 数据通常只包含来自（远大于）总体的样本：我调查了 100 位客户（样本），但我真正感兴趣的是_所有_ 100,000 位客户（总体）。 样本结果通常与总体结果略有不同。 因此，在我的样本中找到非零相关性并不能证明两个变量在我的整个总体中相关； 如果总体相关性确实为零，我很可能在我的样本中发现一个小的相关性。 但是，在这种情况下找到很强的相关性是非常不可能的，这表明我的总体相关性毕竟不为零。

相关性检验 - 假设前提 (Assumptions)

计算和解释相关系数 (correlation coefficients)本身不需要任何假设。 但是，相关性的统计显著性 (statistical significance)检验假设：

SPSS - 快速数据检查

现在让我们在 SPSS 中运行一些相关性检验。 我们将使用 adolescents.sav ，这是一个包含 128 名 12 至 14 岁儿童心理测试数据的数据文件。 下面显示了其变量视图 (variable view) 的一部分。

SPSS 青少年数据变量视图

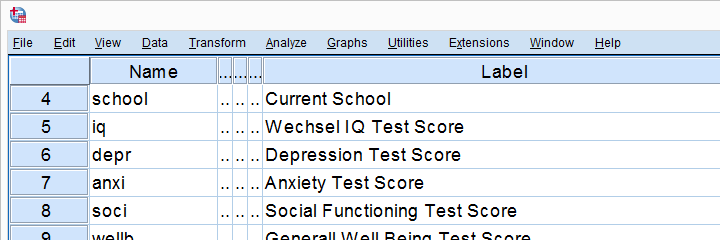
现在，在运行任何相关性之前，让我们首先确保我们的数据首先是合理的。 由于所有 5 个变量都是度量变量，我们将通过运行以下语法 (syntax) 快速检查它们的直方图。

***快速数据检查：所有相关变量的直方图。
**
frequencies iq to wellb
/format notable
/histogram.

直方图输出 (Histogram Output)

我们的直方图告诉我们很多信息：我们的变量有 5 到 10 个缺失值 (missing values) 。 它们的平均值接近 100，标准差约为 15 - 这很好，因为这些测试就是这样校准的。 但有一件事让我感到困扰，如下所示。

SPSS 相关分析直方图异常值

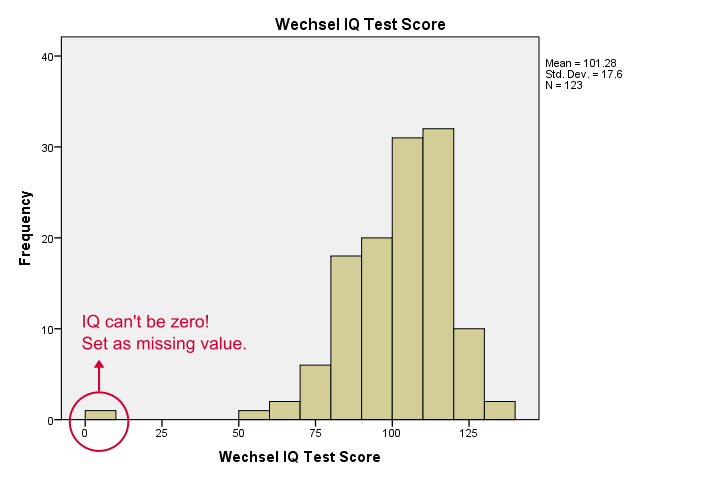
似乎有人在某些测试中得了零分 - 这根本不合理。 如果我们忽略这一点，我们的相关性将受到严重影响。 让我们对我们的案例进行排序，看看发生了什么，并在继续之前设置一些缺失值。

***检查 iq / anxi 分数低的案例。
**
sort cases by iq.

***一个案例在两项测试中的得分为零。 在继续之前设置为缺失值。
**
missing values iq anxi (0).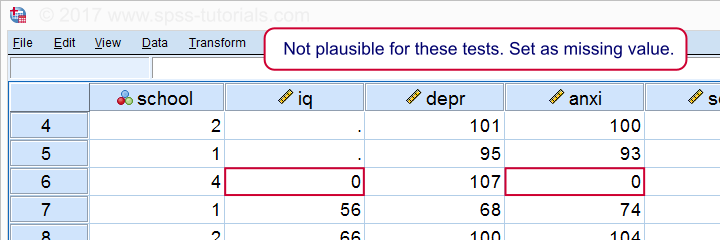

SPSS 数据视图中的相关性异常值

如果我们现在重新运行我们的直方图，我们将看到所有分布看起来都是合理的。 只有现在我们才应该继续运行实际的相关性。

在 SPSS 中运行相关性检验

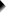首先导航到 A nalyze (分析) SPSS 菜单箭头 C orrelate (相关) SPSS 菜单箭头 B ivariate (双变量) ，如下所示。

SPSS 分析相关双变量

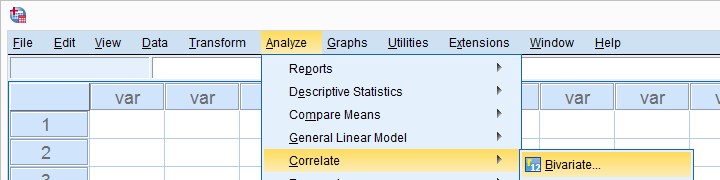
将所有相关变量移动到变量框中。 您可能不想在此处更改任何其他内容。

SPSS 相关性对话框

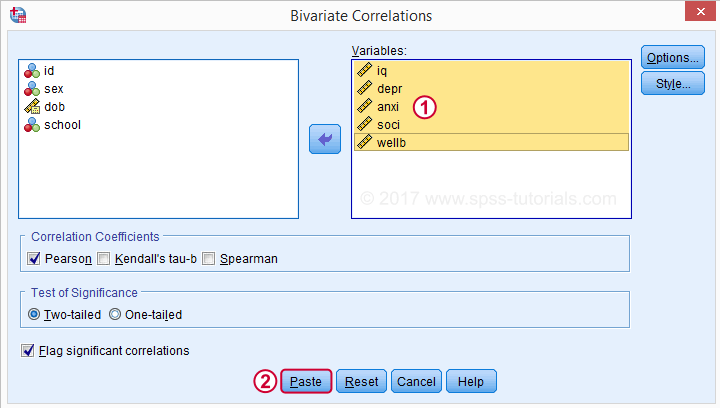
单击 P aste (粘贴) 会生成以下语法。 让我们运行它。

SPSS CORRELATIONS 语法

***从菜单粘贴的相关性。
**
CORRELATIONS
/VARIABLES=iq depr anxi soci wellb
/PRINT=TWOTAIL NOSIG
/MISSING=PAIRWISE.

***较短的版本，创建完全相同的输出。
**
correlations iq to wellb
/print nosig.

相关性输出 (Correlation Output)

SPSS 相关性检验输出

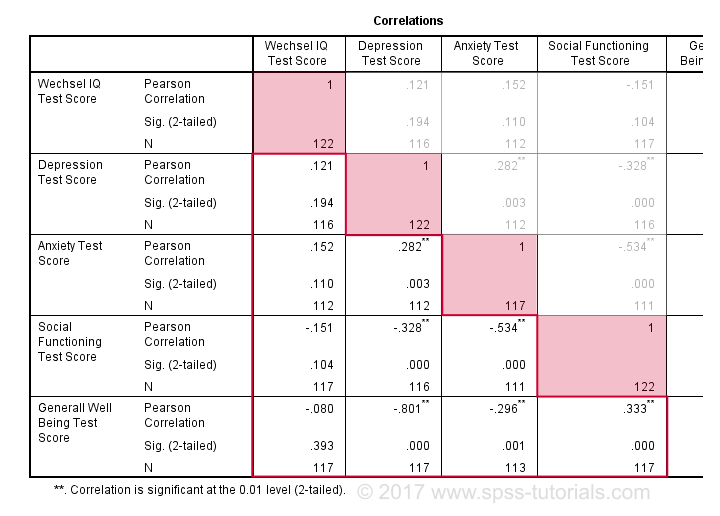
默认情况下，SPSS 始终创建一个完整的相关矩阵。 每个相关性都会出现两次：在主对角线上方和下方。 主对角线上的相关性是每个变量与其自身之间的相关性 - 这就是为什么它们都是 1 并且根本不有趣的原因。 我们需要的是对角线_下方_的 10 个相关性。 根据经验，如果相关性的“Sig. (2-tailed)”< 0.05，则该相关性在统计上显着。 现在让我们仔细看看我们的结果：最强的相关性在抑郁症和整体幸福感之间：r = -0.801。 它基于 N = 117 个孩子，其 双尾显着性 (2-tailed significance) ，p = 0.000。 这意味着如果实际总体相关性为零，则发现此样本相关性 - 或更大的样本相关性的概率为 0.000。

请注意，智商与任何事物都不相关。 它与焦虑症的最强相关性为 0.152，但 p = 0.11，因此它在统计上与零没有显着差异。 也就是说，如果总体相关性为零，则发现它的机会为 0.11。 这种相关性太小，无法拒绝零假设。

像这样，我们的 10 个相关性表明每对变量在多大程度上线性相关。 最后，请注意，每个相关性都是在略有不同的 N 上计算的 - 范围从 111 到 117。 这是因为 SPSS 默认使用成对删除缺失值来计算相关性。

散点图 (Scatterplots)

严格来说，我们还应该检查变量之间的所有 散点图 (scatterplots) 。 毕竟，不相关的变量仍然可能以某种非线性方式相关。 但是，对于超过 5 或 6 个变量，可能的散点图数量会激增，因此我们通常会跳过检查它们。 但是，请参阅 SPSS - 创建所有散点图工具 。

以下语法仅创建一个散点图，只是为了了解我们的关系是什么样的。 但是，结果并没有显示任何意外情况。

***幸福感与抑郁症的简单散点图。
**
graph
/scatter wellb with depr
/subtitle "相关性 = - 0.8 | N = 128".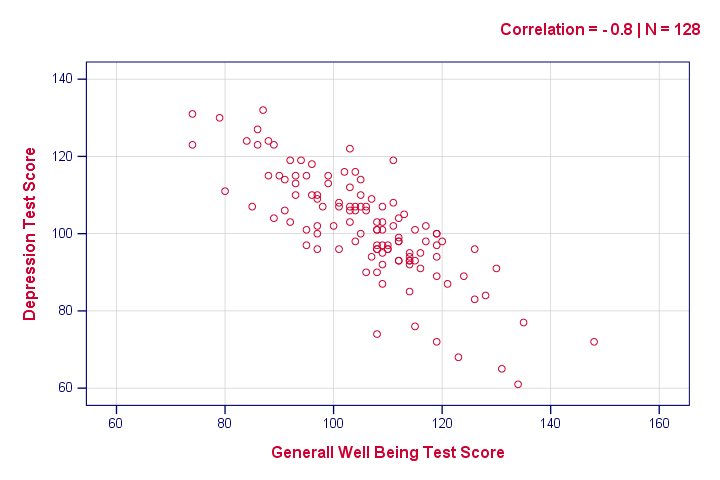

SPSS 相关分析散点图

报告相关性检验

下图显示了 APA 推荐的用于报告相关性的最基本格式。 重要的是，请确保表格指示哪些相关性在 p < 0.05 甚至 p < 0.01 时在统计上显着。 另请参阅 SPSS APA 格式的相关性 。

APA 格式的相关性表

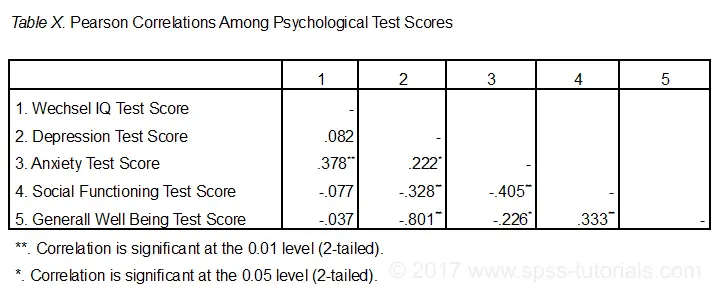
如果可能，也请报告相关性的 置信区间 (confidence intervals) 。 奇怪的是，SPSS 不包含这些内容。 但是，请参阅 SPSS 相关性的置信区间工具 。