独立样本 T 检验 - 快速入门

作者：Ruben Geert van den Berg，归属于 Statistics A-Z 和 T-Tests

独立样本 T 检验 - 是什么？

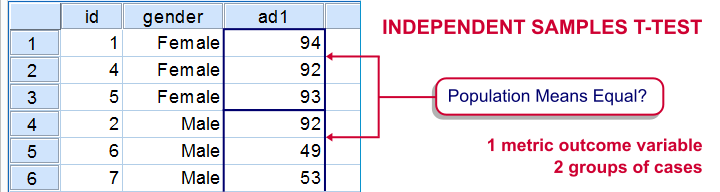
独立样本 T 检验 (Independent Samples T-Test) 用于评估两个总体在某个变量上的均值是否相等。如果总体均值确实相等，那么样本均值可能会略有差异，但不会太大。如果总体均值相等，那么_非常_不同的样本均值不太可能出现。因此，样本结果表明总体均值实际上并不相等。

样本是独立的，因为它们不重叠；没有一个观察值同时属于两个样本。一个典型的例子是男性与女性受访者。

某个岛屿有 1,000 名男性和 1,000 名女性居民。一位研究人员想知道男性每月在电话上花费的时间是多还是少。理想情况下，他会询问所有 2,000 名居民，但这太耗时了。因此，他抽取了 10 名男性和 10 名女性作为样本并询问他们。部分数据如下所示。

接下来，他分别计算男性和女性受访者每月通话分钟数的均值和标准差。结果如下所示。

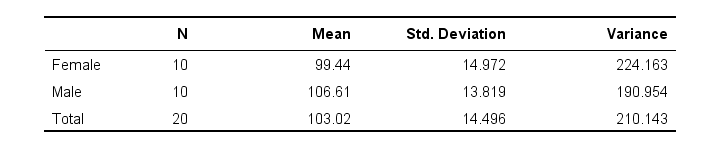
这些样本均值相差约 (99 - 106 =) -7 分钟：平均而言，女性在电话上花费的时间比男性少 7 分钟左右。但这只是我们的小样本。我们能对整个总体说些什么呢？我们将从零假设开始来找出答案。

独立样本 T 检验的零假设（通常）是两个总体均值相等。如果这确实是真的，那么我们可能很容易在我们的样本中找到_略微_不同的均值。那么，我们究竟可以预期什么差异呢？一种直观的找出方法是简单的模拟。

我创建了一个虚假的数据集，其中包含 1,000 名男性和 1,000 名女性的整个总体。平均而言，两组在电话上花费的时间均为 103 分钟，标准差为 14.5。请注意，对于这些总体，均值相等的零假设显然是成立的。

然后，我抽取了 10 名男性和 10 名女性作为样本，并计算了均值差异。然后，我重复了这个过程 999 次，得到了下面显示的 1,000 个样本均值差异。

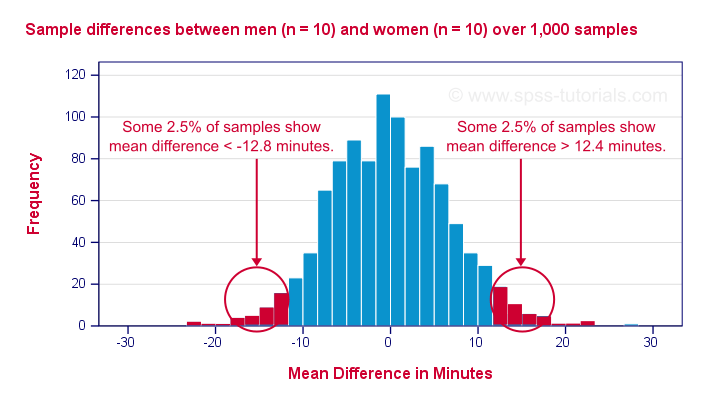
首先，均值差异大致呈正态分布。大多数差异接近于零 - 这并不奇怪，因为总体差异为零。但真正有趣的是，介于 -12.5 和 12.5 之间的均值差异非常常见，占我的 1,000 个结果的 95%。这表明需要 12.5 分钟的绝对差异才能在 α = 0.05 时达到统计显著性。

最后，我们的 1,000 个均值差异的标准差 - 即标准误差 - 为 6.4。请注意，大约 95% 的所有结果都位于我们（零）均值的 -2 和 +2 个标准误差之间。这是关于正态分布的最著名的经验法则之一。

现在，一种更容易 - 尽管不太直观 - 的得出这些结论的方法是使用几个简单的公式。

再次说明：如果总体差异为零，那么“正常”的样本均值差异是多少？首先，这取决于我们结果变量的总体标准差。我们通常不知道它，但我们可以用以下公式估计它：

\[Sw = \sqrt{\frac{(n_1 - 1)\;S^2_1 + (n_2 - 1)\;S^2_2}{n_1 + n_2 - 2}}\]

其中 \(Sw\) 表示我们估计的总体标准差。对于我们的数据，这可以简化为

\[Sw = \sqrt{\frac{(10 - 1)\;224 + (10 - 1)\;191}{10 + 10 - 2}} ≈ 14.4\]

其次，我们的均值差异应该波动较小 - 也就是说，具有较小的标准误差 - 因为我们的样本量较大。标准误差的计算公式为

\[Se = Sw\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}\]

这给了我们

\[Se = 14.4\; \sqrt{\frac{1}{10} + \frac{1}{10}} ≈ 6.4\]

如果总体均值差异为零，那么 - 平均而言 - 样本均值差异也将为零。但是，它的标准差为 6.4。我们现在可以只计算样本均值差异的 z 分数，但 - 由于某种原因 - 它被称为 T 而不是 Z：

\[T = \frac{\overline{X}_1 - \overline{X}_2}{Se}\]

对于我们的数据，这导致

\[T = \frac{99.4 - 106.6}{6.4} ≈ -1.11\]

好的，现在这是我们的检验统计量：一个根据零假设总结我们样本结果的数字。 T 基本上是标准化样本均值差异； T = -1.11 意味着我们的 -7 分钟差异大约低于平均值零 1 个标准差。

我们的 t 值服从 t 分布，但前提是满足以下假设：

独立观察 (Independent observations) 或者，准确地说，是独立且同分布的变量。
正态性 (Normality)：结果变量在总体中服从正态分布。对于合理的样本量（例如，N > 25），不需要此假设。
方差齐性 (Homogeneity)：结果变量在我们的 2 个（子）总体中具有相等的标准差。如果样本量大致相等，则不需要此假设。有时使用 Levene 检验来检验此假设。

如果我们的数据满足这些假设，那么 T 服从自由度 (df) 为 (n1 + n2 - 2) 的 t 分布。在我们的示例中，df = (10 + 10 - 2) = 18。下图显示了精确的分布。请注意，我们需要 2.1 的绝对 t 值才能在 α = 0.05 时达到双尾显著性。

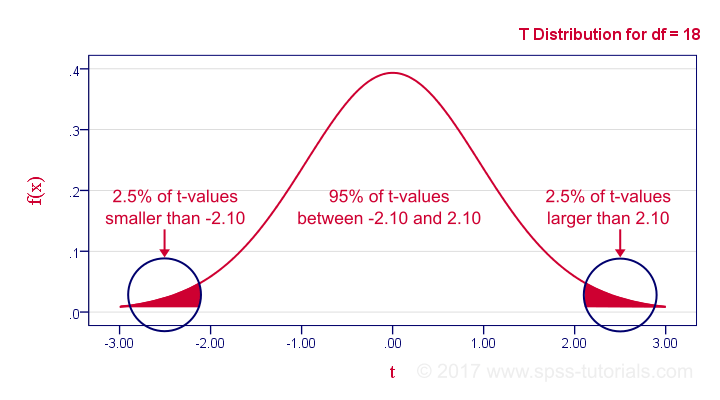
小提示：随着 df 变大，t 分布近似于标准正态分布。如果 df > 15 左右，则差异几乎不明显。

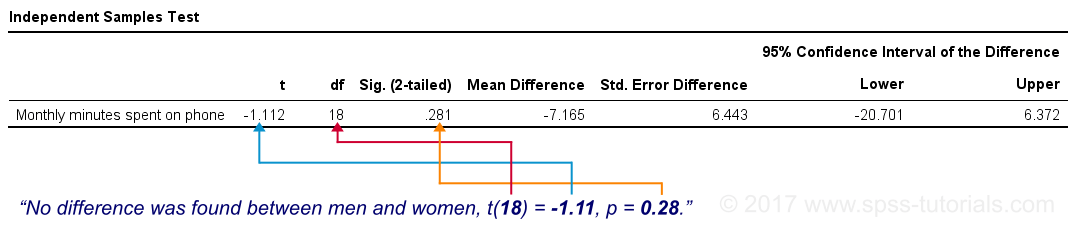
最后但同样重要的是，我们的 -7 分钟的均值差异没有统计显著性：t(18) = -1.11, p ≈ 0.28。这意味着如果我们的总体均值确实相等，那么我们有 28% 的机会找到我们的样本均值差异 - 或更极端的一个差异；这是一个正常的结果，不会与我们的零假设相矛盾。

我们的最终图显示了从 SPSS 获得的结果。

最后，通常首选的效应量度量是 Cohen’s D，定义为

\[D = \frac{\overline{X}_1 - \overline{X}_2}{Sw}\]

其中 \(Sw\) 是我们之前遇到的估计总体标准差。也就是说，Cohen’s D 是两个样本均值之间的标准差数量。那么什么是小的或大的效应呢？已提出以下经验法则：

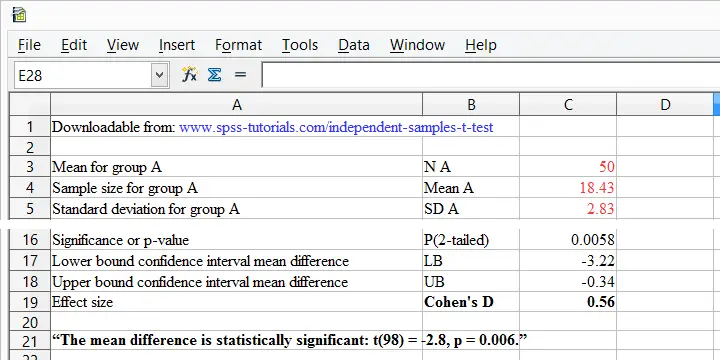
除了 SPSS 27 之外，Cohen’s D 在 SPSS 中令人遗憾地缺失。但是，您可以轻松地从 Cohens-d.xlsx 获取它。只需填写 2 个样本量、均值和标准差，它的公式将计算出您需要知道的一切。

感谢阅读！