SPSS 中位数检验：用于两个独立中位数的比较

作者：Ruben Geert van den Berg，归类于非参数检验 & 统计 A-Z

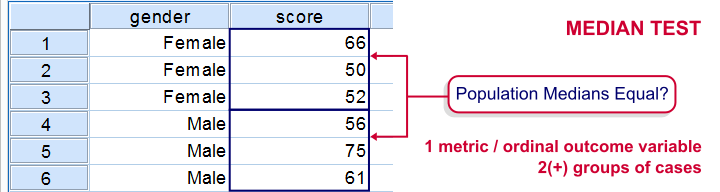
用于独立中位数的中位数检验用于检验两个或多个总体在某个变量上的中位数是否相等。也就是说，我们一次比较 2 个或更多组的个案在一个变量上的表现。

汽车广告评分

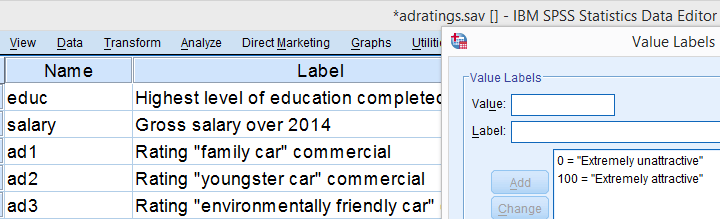
我们将使用 adratings.sav 文件来演示中位数检验。该文件包含 18 名受访者对 3 个不同汽车广告吸引力的评分数据。评分使用百分比尺度，从 0（极具吸引力的广告）到 100（极具吸引力的广告）。

中位数检验 - 零假设 (Null Hypothesis)

一位营销人员想知道男性对这 3 个广告的评分是否与女性不同。在使用 Mann-Whitney 检验比较平均分后，他还想知道中位数是否相等。中位数检验将通过检验零假设来回答这个问题，即男性和女性在每个评分变量上的总体中位数相等。

中位数检验 - 假设 (Assumptions)

中位数检验只有两个假设：

独立的观测值（或更准确地说，独立且同分布的变量）；
检验变量是定序的或度量的（即，不是名义的）。

快速数据检查

adratings 数据没有包含任何奇怪的值或模式。如果您正在分析任何其他数据，请确保始终从数据检查开始。至少，运行一些直方图并检查缺失值。

中位数检验 - 描述性统计 (Descriptives)

好的，我们正在比较 2 组个案在 3 个评分变量上的表现。让我们首先看一下结果的 6 个中位数。最快的方法是运行一个基本的 MEANS 命令。

*检查男性和女性的中位数，分开查看。.
MEANS ad1 to ad3 BY gender
/CELLS COUNT MEAN MEDIAN.

结果

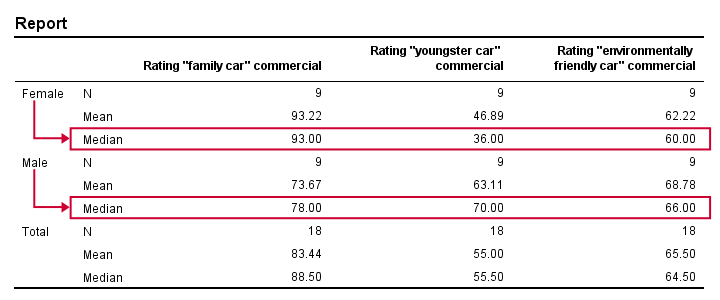
基本上，“家庭用车”广告的评分更高。男性更喜欢“年轻人用车”广告。“环保汽车”广告在两个性别之间的评分大致相似 - 至少从中位数来看是这样。

现在，请记住这只是一个小样本。如果总体中位数完全相等，那么由于随机抽样波动，我们可能会在样本中找到略有不同的中位数。但是，非常不同的样本中位数表明总体中位数毕竟不相等。中位数检验告诉我们，考虑到我们的样本中位数，相等的总体中位数是否可信。

SPSS 中的中位数检验

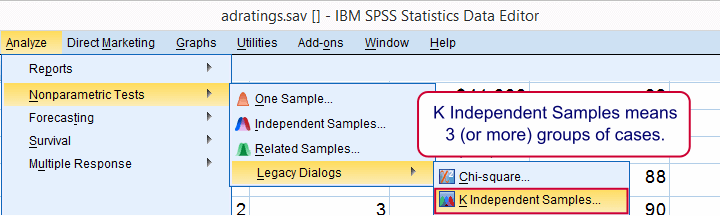
通常，比较 2 个统计量与比较 3 个及以上统计量使用的检验方法不同。例如，我们使用独立样本 t 检验比较 2 个独立平均值，使用单因素方差分析 (one-way ANOVA) 比较 3 个及以上独立平均值。我们使用配对样本 t 检验比较 2 个相关平均值，使用重复测量方差分析 (repeated measures ANOVA) 比较 3 个及以上相关平均值。我们使用 McNemar 检验比较 2 个相关比例，使用 Cochran Q 检验比较 3 个及以上相关比例。中位数检验是一个例外，因为它用于比较 2 个或更多个独立中位数。这就是为什么我们选择 K 独立样本而不是 2 独立样本来比较 2 个中位数的原因。

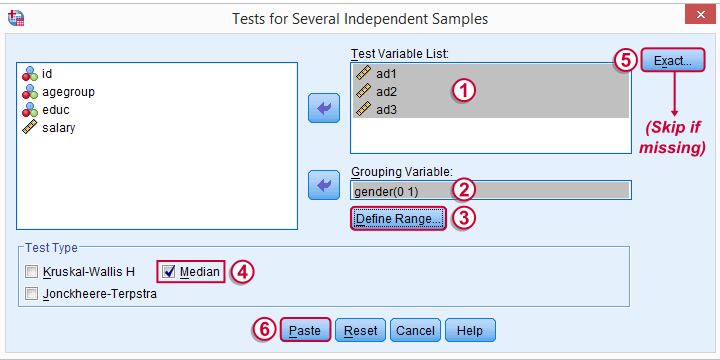
根据您的 SPSS 许可，精确 (Exact) 按钮可能不存在。如果存在，请按如下所示填写。

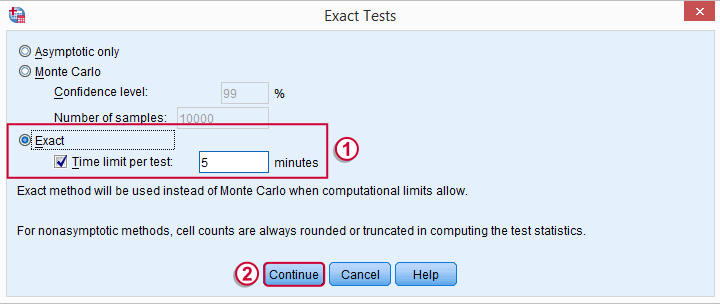
SPSS 中位数检验语法

完成这些步骤将产生以下语法（如果您选择了精确检验，则会有一行额外的代码）。

*用于独立中位数的基本中位数检验。.
NPAR TESTS
/MEDIAN=ad1 ad2 ad3 BY gender(0 1)
/MISSING ANALYSIS.

中位数检验 - 基本原理

在检查我们的输出之前，让我们首先了解一下该检验如何针对一个变量工作。中位数检验首先计算一个变量的中位数，而不管我们要比较的组是什么。接下来，如果每个个案（数据值的行）的分数 > 总体中位数，则会对其进行标记。最后，我们将查看得分 > 中位数是否与性别相关，通过一个基本的交叉表。您可以使用 AGGREGATE、IF 和 CROSSTABS 轻松地自行运行这些步骤。

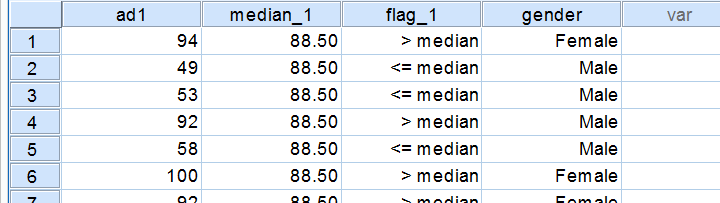
中位数检验输出 - 交叉表 (Crosstabs)

请注意，这些结果与我们之前运行的中位数一致。我们对“家庭用车”广告的结果尤其引人注目：在评分高于（总体）中位数的 9 名受访者中，有 8 名是女性。

中位数检验输出 - 检验统计量 (Test Statistics)

如果我们的总体中位数在性别之间相等，这些是否是正常的结果？对于我们的第一个广告，p = 0.003，表明观察到此结果的几率为 1/1000。由于 p < 0.05，我们得出结论，对于“家庭用车”广告，总体中位数不相等。

其他两个广告的 p 值 > 0.05，因此这些发现并未驳斥总体中位数相等的零假设。

这就是目前的基本内容。但是，我们想对那些感兴趣的人更详细地讨论 p 值。

Asymp. Sig. (渐近显著性)

在本例中，我们获得了精确的 p 值。但是，当在较大的样本上运行此检验时，您可能会在输出中找到“渐近显著性 (Asymp. Sig.)”。这是一个基于卡方统计量和相应自由度 (df, degrees of freedom) 的近似 p 值。有时会使用这种近似值，因为精确的 p 值计算起来很麻烦，尤其是对于较大的样本量。

精确 P 值 (Exact P-Values)

那么，精确的 p 值来自哪里？它们与我们在此处看到的列联表有什么关系？嗯，左上角单元格中的频率遵循超几何分布。如下图所示，显示了第二个 p 值 0.347 的来源。

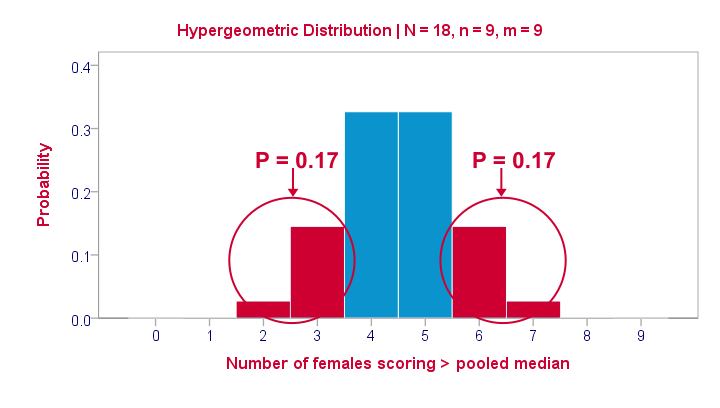
在零假设下 - 性别和得分 > 中位数是独立的 - 最可能的结果是 4 或 5，每个结果的概率约为 0.33。3 或更少的概率约为 0.17。这是我们的单尾 p 值。我们的双尾 p 值考虑了找到 6 或更多值的 0.17 的概率，因为这也会与我们的零假设相矛盾。

该图还说明了为什么我们的第三个检验的双尾 p 值为 1.000：4 或更少以及 5 或更多的概率涵盖了所有可能的结果。关于我们的第一个测试，1 或更少以及 8 或更多的概率接近于零（精确地说：0.003）。

使用交叉表 (CROSSTABS) 进行中位数检验

好的，所以前面的图解释了精确 p 值如何基于超几何分布。此过程称为 Fisher 的精确检验，当运行卡方独立性检验时，您可能已经在 SPSS CROSSTABS 输出中看到过它。而且 - 实际上 - 您也可以从 CROSSTABS 中获得我们独立中位数检验的精确 p 值。事实上，您甚至可以使用 compute p2 = 2* cdf.hyper(3,18,9,9). execute. 在数据中将其计算为一个新变量，该命令返回 0.347，这是我们第二个广告的 p 值。

感谢阅读！

参考文献

Siegel, S. & Castellan, N.J. (1989). Nonparametric Statistics for the Behavioral Sciences (2nd ed.). Singapore: McGraw-Hill.
Van den Brink, W.P. & Koele, P. (2002). Statistiek, deel 3 [统计学，第 3 部分]。 Amsterdam: Boom.