Kruskal-Wallis 检验 – 简易教程
By Ruben Geert van den Berg under Statistics A-Z
- Kruskal-Wallis 检验示例
- Kruskal-Wallis 检验假设
- Kruskal-Wallis 检验公式
- Kruskal-Wallis 事后检验 (Post Hoc Tests)
- APA 格式报告 Kruskal-Wallis 检验
Kruskal-Wallis 检验用于检验 3 个或更多个总体在某个结果变量上的平均秩是否相等。下图说明了基本思想。
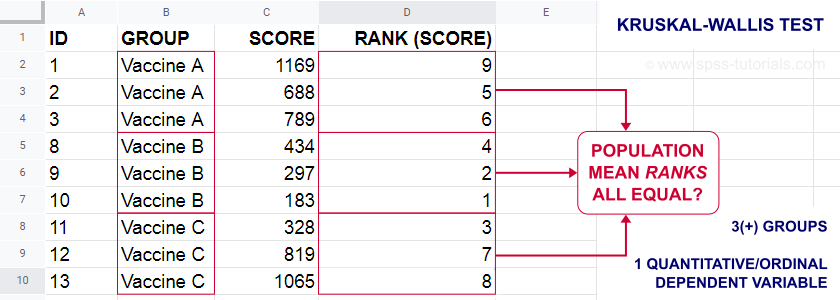
- 首先，对所有分数进行升序排列，不考虑组别。
- 如果分数与组别无关，那么各组的平均秩应该大致相等。
- 如果样本中各组的平均秩差异很大，那么某些组在总体中也倾向于具有比其他组更高的分数：分数与组别相关。
Kruskal-Wallis 检验 - 目的
Kruskal-Wallis 检验是 方差分析 (ANOVA) 的一种非参数替代方法：我们基本上想知道 3 个或更多个总体在某个变量上的均值是否相等。但是，
- 如果因变量是顺序变量，则不适合使用方差分析 (ANOVA)；
- 方差分析 (ANOVA) 要求因变量在每个子总体中 服从正态分布，尤其是在样本量较小时。
如果样本量较小和/或因变量是顺序变量，则 Kruskal-Wallis 检验是方差分析 (ANOVA) 的合适替代方法。
Kruskal-Wallis 检验示例
一家医院对 3 种疫苗进行快速试验：每种疫苗给 N = 5 名参与者接种。一周后，他们测量参与者血液中的抗体量。获得的数据位于 此 Google 表格 中，部分内容如下所示。
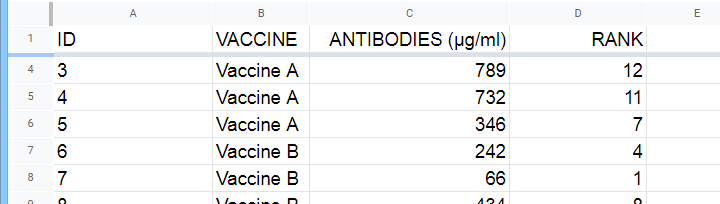
现在，我们想知道在潜在的总体中，是否有些疫苗比其他疫苗能激发更多的抗体。由于抗体是一个定量变量，因此方差分析 (ANOVA) 似乎是这里的正确选择。
但是，方差分析 (ANOVA) 要求抗体在每个子总体中服从正态分布。并且由于我们的最小样本量，我们不能像通常那样（或者_应该_）依赖中心极限定理。最重要的是，我们的样本量太小，无法检查正态性。为了强调这一点，下面显示了按组别划分的抗体直方图。
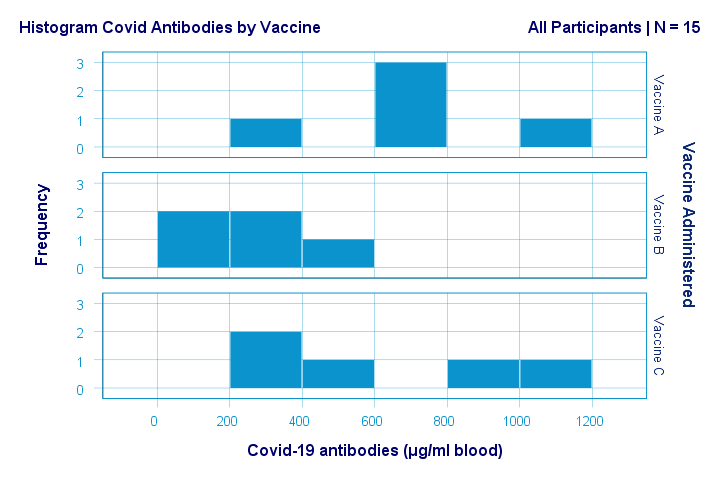
如果有什么不同的话，底部的两个直方图似乎略微 正偏斜。这是有道理的，因为抗体量有一个下限零，但没有上限。但是，关于总体分布的推测不会比这更严肃。
这里一个特别糟糕的主意是试图通过运行以下测试来证明正态性：
由于我们的样本量很小，这些测试不太可能拒绝正态性的零假设。但是，这仅仅是由于它们缺乏功效，并且没有说明总体分布的任何信息。换句话说：对于完全相同的数据，不同的零假设（我们的变量服从均匀分布或泊松分布）可能也不会被拒绝。
简而言之：方差分析 (ANOVA) 确实需要小样本量下的正态性，但我们不知道它是否成立。所以我们不能信任方差分析 (ANOVA) 的结果。这就是我们应该使用 Kruskal-Wallis 检验的原因。
Kruskal-Wallis 检验 - 零假设
Kruskal-Wallis 检验的零假设是：在 3 个或更多个总体中，某个结果变量的平均秩是相等的。请注意，结果变量必须是顺序变量或定量变量，这样“平均秩”才有意义。
许多教科书提出了一个不正确的零假设，例如：
- 某个结果变量在 3 个或更多个总体中具有相等的 中位数 或
- 某个结果变量在 3 个或更多个总体中遵循相同的分布。
那么，为什么这些是不正确的呢？好吧，Kruskal-Wallis 公式仅使用 2 个统计量：秩和以及它们所基于的样本量。它完全忽略了关于数据的其他所有内容——包括中位数和频率分布。这些都不会影响零假设是否被拒绝。
如果这仍然不能说服你，我们可能会向本教程添加一些示例数据文件。这些例子说明了截然不同的中位数或频率分布并不总是导致“显着”的 Kruskal-Wallis 检验（或者反之）。
Kruskal-Wallis 检验假设
Kruskal-Wallis 检验需要 3 个假设 1 , 5 , 8 :
- 独立观察；
- 因变量必须是定量变量或顺序变量；
- 足够的样本量（例如，每个 n i ≥ 5），_除非_计算精确的显着性水平。
关于最后一个假设，可以计算 Kruskal-Wallis 检验的精确 p 值。然而，这种情况很少发生，因为它通常需要非常繁重的计算。一些精确的 p 值也可以在 Use of Ranks in One-Criterion Variance Analysis 中找到。
相反，大多数软件计算基于卡方分布的近似（或“渐近”）p 值。如果样本量足够大，则此近似值足够准确。对于所需的样本量，没有真正的共识：一些作者 1 提出每个 n i ≥ 4，而另一些作者 6 建议每个 n i ≥ 6。
Kruskal-Wallis 检验公式
首先，我们将因变量的值进行升序排列，不考虑组别。我们在 此 Google 表格 中完成了此操作，部分内容如下所示。
接下来，我们分别计算每个组的所有秩的和。
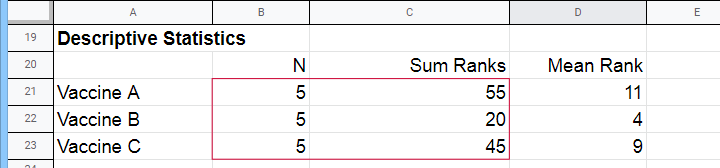
然后，我们将 a) 我们的样本量和 b) 我们的秩和输入到以下公式中：
\[Kruskal\;Wallis\;H = \frac{12}{N(N + 1)}\sum\limits_{i = 1}^k\frac{R_i^2}{n_i} - 3(N + 1)\]
其中
- \(N\) 表示总样本量；
- \(k\) 表示我们要比较的组数；
- \(R_i\) 表示组 \(i\) 的秩和；
- \(n_i\) 表示组 \(i\) 的样本量。
对于我们的示例，这将是
\[Kruskal\;Wallis\;H = \frac{12}{15(15 + 1)}(\frac{55^2}{5}+\frac{20^2}{5}+\frac{45^2}{5}) - 3(15 + 1) =\]
\[Kruskal\;Wallis\;H = 0.05\cdot(605 + 80 + 405) - 48 = 6.50\]
\(H\) 近似服从具有
\[df = k - 1\]
自由度 (\(df\)) 的卡方（写为 χ 2 ）分布，其中 \(k\) 表示组数。对于我们的示例，
\[df = 3 - 1 = 2\]
所以我们的 显着性水平 是
\[\chi^2(2) = 6.50, p \approx 0.039.\]
SPSS 输出（如下所示）证实了我们的计算。
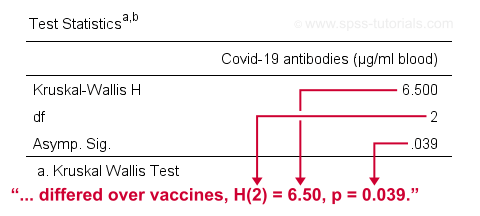
那么我们现在得出什么结论呢？好吧，假设 alpha = 0.05，我们拒绝我们的零假设：抗体的总体平均秩在疫苗之间是不相等的。用正常语言来说，我们的 3 种疫苗表现_不_一样好。从平均秩来看，似乎 B 疫苗的表现比竞争对手差：它的平均秩较低，这意味着它激发的抗体比其他疫苗少。
Kruskal-Wallis 事后检验 (Post Hoc Tests)
到目前为止，我们得出的结论是，抗体的量在我们的 3 种疫苗之间是不同的。那么，究竟哪种疫苗与哪种疫苗不同呢？我们将比较每种疫苗与_其他_疫苗，以找出答案。此过程通常称为运行事后检验 (post-hoc tests)。
与普遍的看法相反，Kruskal-Wallis 事后检验 (post-hoc tests) 不等同于 Bonferroni 校正的 Mann-Whitney 检验 。相反，使用以下公式比较每种可能的组对：
\[Z_{kw} = \frac{\overline{R}_i - \overline{R}_j}{\sqrt{\frac{N(N + 1)}{12}(\frac{1}{n_i}+\frac{1}{n_j})}}\]
其中
- 我们的检验统计量 \(Z_{kw}\) 近似服从 标准正态分布；
- \(R_i\) 表示组 \(i\) 的平均秩；
- \(N\) 表示总样本量（包括未在此成对比较中使用的组）；
- \(n_i\) 表示组 \(i\) 的样本量。
对于比较 A 和 B 疫苗，这将是
\[Z_{kw} = \frac{11 - 4}{\sqrt{\frac{15(15 + 1)}{12}(\frac{1}{5}+\frac{1}{5})}} \approx 2.475 \]
\[P(|Z_{kw}| > 2.475) \approx 0.013\]
通常将 Bonferroni 校正 应用于此 p 值，因为我们对（部分）相同的观察值进行多次比较。\(k\) 组的成对比较次数为
\[N_{comp} = \frac{k (k - 1)}{2}\]
因此，我们的示例的 Bonferroni 校正 p 值为
\[P_{Bonf} = 0.013 \cdot \frac{3 (2 - 1)}{2} \approx 0.040\]
来自 SPSS 的屏幕截图（如下）证实了这些发现。
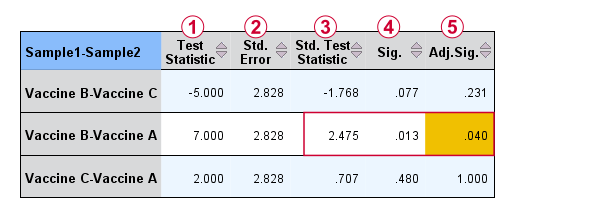
奇怪的是，平均秩之差 \(_i - j\) 被表示为“检验统计量 (Test Statistic)”。 
实际的检验统计量 \(Z{kw}\) 被表示为“标准检验统计量 (Std. Test Statistic)”。
APA 格式报告 Kruskal-Wallis 检验
对于 APA 格式报告我们的示例分析，我们可以这样写：“Kruskal-Wallis 检验表明，抗体的量在疫苗之间存在差异，H(2) = 6.50, p = 0.039。”
虽然 APA 没有提及，但我们鼓励在单独的表格中报告平均秩，或许还有一些其他描述性统计量。
