SPSS 双因素方差分析基础教程

作者：Ruben Geert van den Berg 在 ANOVA 栏目下

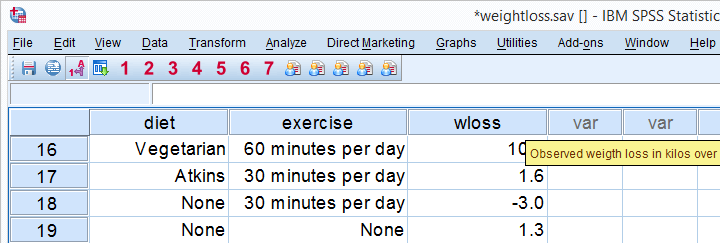
研究问题

如何有效减肥？饮食真的有效吗？运动呢？为了找出答案，180 名参与者被分配到 3 种不同的饮食方案和 3 种不同的运动水平。两个月后，参与者被问及他们减掉了多少公斤。这些数据（如上图所示的部分）位于 weightloss.sav 文件中。我们将检验在两个月后，不同饮食、运动水平以及饮食与运动水平的每种组合的平均减重量是否相同。也就是说，我们将比较两个以上的平均值，因此我们将使用某种方差分析（ANOVA）。

案例计数和直方图

在进行任何分析之前，我们总是希望对数据有一个基本的了解。我们首先要确认我们确实有 180 个案例。接下来，我们想用直方图检查减重量的频率分布。我们将通过运行以下语法来实现这一点。

***检查我们有多少个案例。
**
show n.

***检查减重量的直方图。
**
frequencies wloss
/format notable /*= 不要创建表格，因为它太大了。
/histogram.

结果

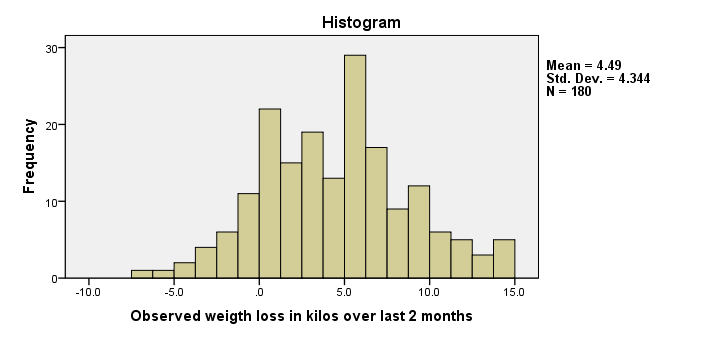
我们确实有 180 个案例。重要的是，减重量的直方图看起来是合理的。我们没有看到任何应该设置为用户缺失值的非常高或非常低的值。一两个参与者增加了大约 7 公斤（减重量 = -7），有些人设法减掉了多达 15 公斤。此外，减重量看起来相当正态分布。

饮食与运动的列联表（Contingency Table）

现在我们想知道参与者在饮食和运动中的分布情况。对于我们后面的方差分析（ANOVA），我们需要知道我们的设计是否平衡：每个运动水平上的饮食参与者百分比是否相等？你们中的一些人可能会注意到，这个问题实际上是卡方检验中的零假设。这正是我们接下来要运行的。

***查看参与者在饮食*运动组中的分布情况。
**
crosstabs diet by exercise
/statistics chisq.

结果

请注意，每个单元格（饮食和运动水平的组合）包含 20 名参与者。请注意，我们的 卡方值（chi-square value）为 0（未在屏幕截图中显示）。这意味着我们正在处理一个平衡的设计，这是一件好事，因为不平衡的设计会使双因素方差分析（two-way ANOVA）变得复杂。

均值表（Means Table）

那么饮食和运动有效果吗？获得这个想法的一个非常简单的方法是运行一个基本的 MEANS 表。

***检查饮食、运动和饮食*运动的均值。
**
means wloss by diet by exercise.

结果

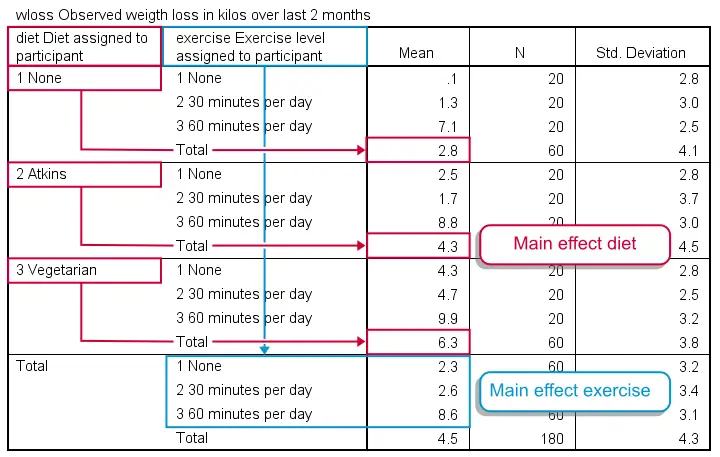
可能需要一分钟才能看到此表中的模式，但我尽力用颜色突出显示它。请注意，没有任何饮食的参与者（所有运动水平加在一起）平均减掉了 2.8 公斤。阿特金斯饮食（Atkins diet）和素食饮食（vegetarian diets）平均导致 6.3 公斤和 4.3 公斤的减重量。这是饮食的主效应（main effect）：在考虑所有运动水平时，归因于饮食的减重量差异。以类似的方式，我们看到运动的主效应略强，平均值从 2.3 公斤到 8.6 公斤不等。一个有趣的问题是 运动的效果 是否取决于所遵循的饮食。这就是我们所说的 交互效应（interaction effect）。我们将在稍后通过在图表中可视化我们的均值来解释它。

双因素方差分析（Two Way ANOVA）- 基本思想

我们刚刚看到，不同的饮食和运动水平显示出不同的平均减重量。但是，我们只看了一个很小的样本。在（大得多的）总体中的情况可能不同。如果饮食和运动在我们的人群中没有任何影响，我们发现这些差异是否可信？我们将通过运行双因素方差分析来回答这个问题。

方差分析（ANOVA）假设

简而言之，方差分析（ANOVA）所需的主要统计假设是：

独立观察（independent observations）：这通常意味着每个案例（数据值的行）必须代表一个单独的人（或其他“对象”）。不允许一个人以多个案例的形式出现，这对我们的数据成立。
方差齐性（homoscedasticity）：我们的因变量（减重量）的标准差对于每个（饮食/运动）的受访者组必须相等。我们之前的均值表显示它们确实非常相似。尽管如此，我们还将使用 Levene 检验更正式地检验这个假设，该检验包含在 SPSS 方差分析过程中。
正态分布 的总体中的因变量。我们之前的直方图表明这适用于我们的数据。最重要的是，由于中心极限定理，对于较大的样本量，正态性假设的重要性较小。

SPSS 双因素方差分析（Two Way ANOVA）菜单

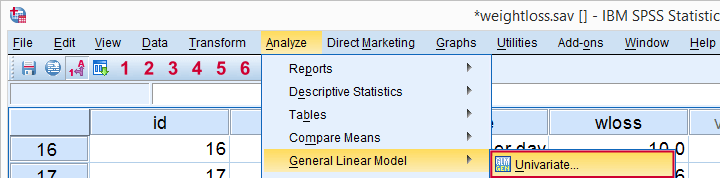
每当我们只分析一个因变量（减重量）时，我们选择 U nivariate，无论我们有多少个自变量（饮食和运动）。

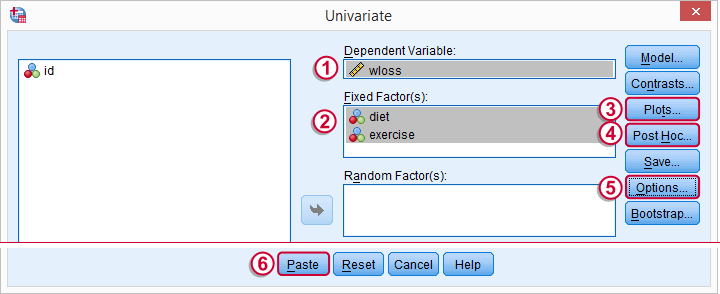
在粘贴语法之前，我们将快速跳转到子对话框，和以调整一些设置。

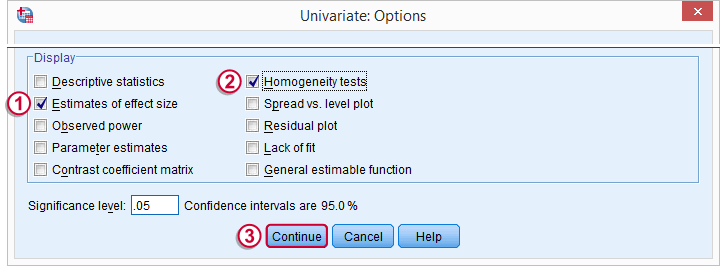
效应大小的估计（Estimates of effect size）将在我们的输出中添加偏 eta 方。方差齐性检验（Homogeneity tests）是指 Levene 检验。它评估我们因变量的总体方差在我们因素的水平上是否相等。这是方差分析（ANOVA）所必需的假设。

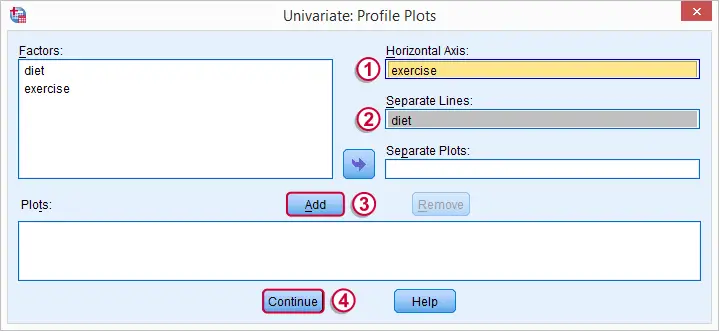
剖面图（Profile plots）可视化了每个因素组合的均值。正如我们稍后将看到的，这可以深入了解我们的因素如何与我们的因变量相关联，并且可能在这样做时相互作用。

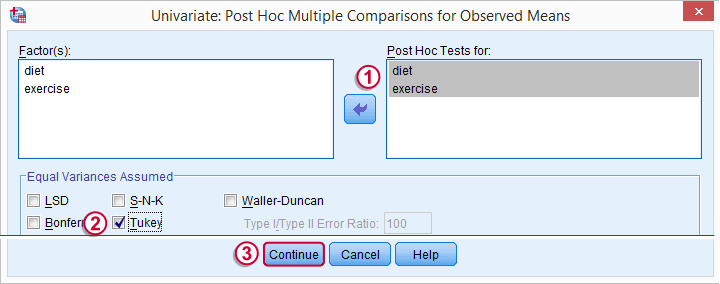
基本的方差分析（ANOVA）仅检验所有均值相等的零假设。如果这不太可能，那么我们通常想知道哪些均值不相等。用于找出答案的最常见的事后检验（post hoc test） 是 Tukey 的 HSD（代表 Honestly Significant Difference，真诚显著性差异）。

SPSS 双因素方差分析语法

完成所有步骤将得到以下语法。我们将运行它并讨论结果。

***带有均值图、Tukey 事后检验、Levene 检验和偏 Eta 方的方差分析。
**
UNIANOVA wloss BY diet exercise
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=diet exercise (TUKEY)
/PLOT=PROFILE(exercise*diet)
/PRINT=ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=diet exercise diet*exercise.

双因素方差分析输出 - Levene 检验

Levene 检验不拒绝以后用于我们的方差分析结果所需的方差相等假设。 我们可以开始了。现在让我们向下滚动到输出的末尾，首先查看我们的剖面图（profile plots）。

双因素方差分析输出 - 剖面图（Profile Plots）

双因素方差分析基础 - 均值图

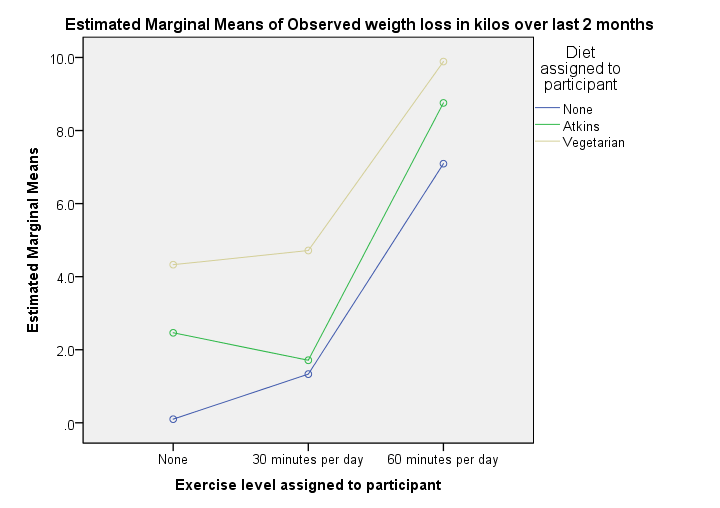
这基本上说明了一切。我们看到每条线在每天 30 到 60 分钟的运动之间急剧上升。其次，素食饮食总是比其他饮食导致更多的减重量。饮食和运动似乎对减重量都有主效应（main effect）。那么我们的交互效应（interaction effect） 呢？好吧，运动的效果被可视化为每个饮食组的一条单独的线。由于这些线看起来非常相似，因此我们的图没有显示出太多的交互效应。但是，我们将在稍后尝试通过更正式的测试来确认这一点。技术说明：“估计边际均值（estimated marginal means）”等于我们之前均值表中的观察均值，因为我们测试了饱和模型（saturated model）（包括所有主效应和交互效应，因为这是 UNIANOVA 中的默认设置）。

双因素方差分析输出 - 主体间效应检验（Tests of Between-Subjects Effects）

我们的均值图对于描述我们样本中由饮食和运动产生的均值模式非常有用。但是，也许在更大的总体中情况有所不同。如果饮食和运动都不影响减重量，我们能否通过单纯的抽样波动（sampling fluctuation）找到这些样本结果？简短的回答：不能。

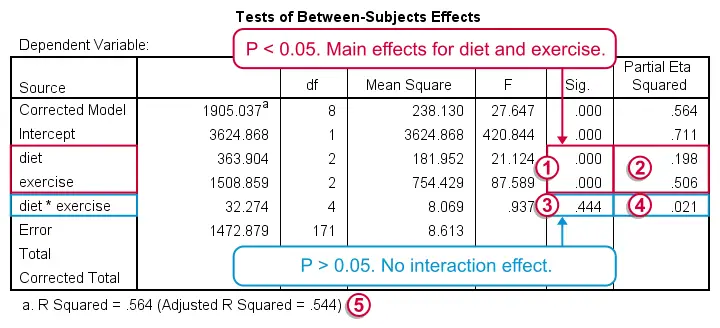
在主体间效应检验中，我们对 3 行 感兴趣：我们的 2 个主效应（饮食和运动）和 1 个交互效应（饮食 * 运动）。我们通常忽略其他行，例如“修正模型（Corrected Model）”和“截距（Intercept）”。首先是交互作用（interaction）：如果运动的效果对于所有饮食都相同，那么找到我们的样本结果的概率为 0.44（p 值，在“显著性（Sig）”下表示“显著性”）。我们通常分别报告 3 个效应中的每一个的 df（“自由度（degrees of freedom）”）、F 值和 p 值：“饮食和运动之间的交互作用无法证明，F(4,171) = .94, p = 0.44。” 此外，请注意，对于我们的交互作用，偏 eta 方 仅为 0.021。这基本上可以忽略不计。当且仅当没有交互作用时，我们才会研究主效应（main effect），两者的 p = 0.000：如果在我们更大的总体中没有主效应，则找到这些样本主效应的概率基本上为零。 偏 eta 方（Partial eta squared） 对于运动为 0.51，对于饮食为 0.20。也就是说，运动的相对影响是饮食的两倍以上。最后但并非最不重要的一点是，调整后的 r 平方（adjusted r squared） 告诉我们，减重量的 54.4% 的方差可归因于饮食和运动。在社会科学研究中，这是一个很高的值，表明我们的因素与减重量之间存在很强的关系。

双因素方差分析输出 - 多重比较（Multiple Comparisons）

我们现在知道，所有不同饮食和运动水平的平均减重量不相等。那么哪些均值是不同的呢？我们可以通过事后检验（post hoc tests）来解决这个问题，其中最常见的是 Tukey 的 HSD，其输出如下所示。

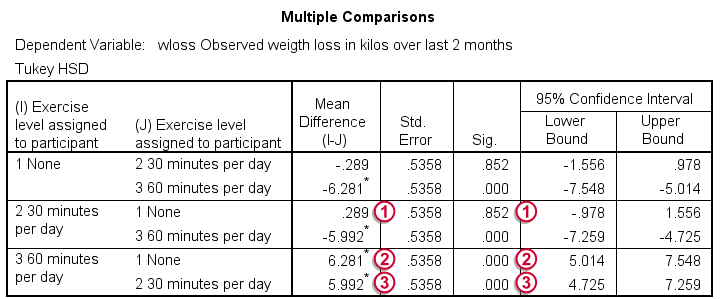
对于 3 个均值，进行 3 次比较（a-b、b-c 和 a-c）。每次都在此表中报告两次，从而产生 6 行。没有运动和 30 分钟运动之间的减重量差异为 0.29 公斤。如果在我们更大的总体中为零，那么在我们的样本中找到这个值的概率为 85.2%。我们的结果没有证明与没有运动相比，30 分钟运动的任何效果。没有运动和 60 分钟运动之间的差异高达 6.28 公斤。星号 (*)、置信区间和 p 值都表明该差异在统计上显着。输出中出现了类似的饮食表，但我们将把它作为练习留给读者来解释。