重复测量方差分析（Repeated Measures ANOVA）- 简易入门

作者：Ruben Geert van den Berg 分类：方差分析 (ANOVA) & 统计学 A-Z

零假设 (Null Hypothesis)
假设前提 (Assumptions)
案例 (Example)
重复测量方差分析 - 基本公式 (Repeated Measures ANOVA - Basic Formulas)
事后检验 (Post Hoc Tests)

零假设 (Null Hypothesis)

重复测量方差分析的零假设 (null hypothesis) 是指：在某个总体中，3个或更多个度量变量具有相同的均值。

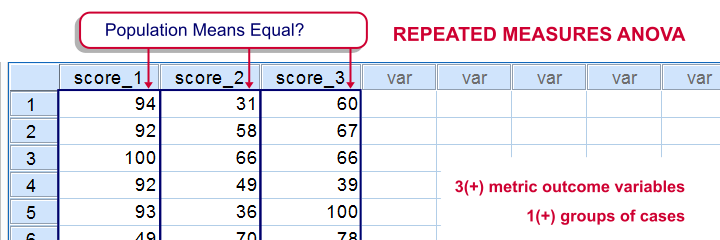
这些变量是在同一批受试者上测量的，因此我们关注的是受试者内效应 (within-subjects effects) （均值之间的差异）。这种基本思想在例如非参数检验 (nonparametric tests)中也被称为相关样本 (related samples)，配对样本 (paired samples) 或相关样本 (dependent samples)。但无论如何，如果所有总体均值 वास्तव में 相等，我们可能会在一个来自该总体的样本中发现略微不同的均值。然而，在这种情况下，非常不同的样本均值是不太可能出现的。这些差异表明总体均值从一开始就不相等。 重复测量方差分析 (Repeated measures ANOVA) 主要告诉我们，如果所有总体均值都相等，我们的样本均值差异的可能性有多大。

重复测量方差分析 - 假设前提 (Repeated Measures ANOVA - Assumptions)

独立观察 (Independent observations)，或者更准确地说，独立同分布变量 (Independent and identically distributed variables)；
正态性 (Normality)：检验变量在总体中服从多元正态分布 (normal distribution)；
球形性 (Sphericity)：检验变量之间所有差值分数 (difference scores) 的方差在总体中必须相等。球形性有时通过 Mauchly’s test (Mauchly 球形检验) 进行检验。如果球形性被拒绝，可以使用 Huynh-Feldt 校正或 Greenhouse-Geisser 校正来修正结果。

重复测量方差分析 - 基本思想 (Repeated Measures ANOVA - Basic Idea)

稍后我们将展示一些案例计算 (example calculations)。但首先：重复测量方差分析 基本上 是如何工作的？首先，我们的结果变量在受试者之间和受试者内部都会发生变化。也就是说，受试者之间和受试者内部的差异加起来就是分数之间的总变异量 (total amount of variation)。这个变异量表示为 SS total，其中 SS 是 “sums of squares（平方和）” 的缩写。

然后，我们将总方差分解为各个组成部分，并检查哪个组成部分解释了多少方差，如下所示。请注意，“df” 表示 “自由度 (degrees of freedom)”，我们稍后会介绍。

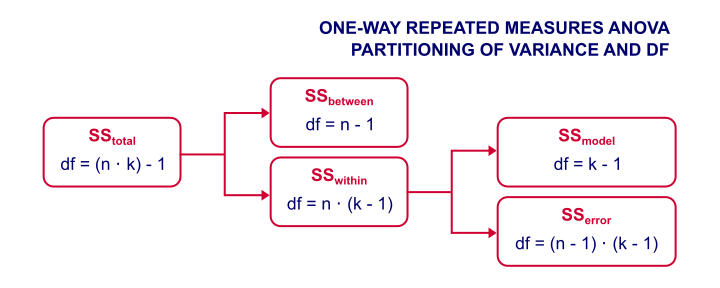
现在，我们对受试者之间的分数差异不感兴趣。因此，我们从总方差中移除此方差并忽略它。然后，我们只剩下 SS within （受试者内部的变异）。

受试者内部的变异可能部分是由于我们的变量具有不同的均值。这些不同的均值构成了我们的模型。 SS model 是它解释的变异量。

接下来，我们的模型通常不能解释受试者内部分数的所有变异。 SS error 是我们的模型未能解释的方差量。

最后，我们比较两个方差来源：如果 SS model 很大，而 SS error 很小，那么受试者内部的变异主要是由于我们的模型（由不同的变量均值组成）。这将导致一个较大的 F 值，如果总体均值确实相等，这种情况是不太可能发生的。在这种情况下，我们将拒绝零假设，并得出总体均值毕竟不相等的结论。

重复测量方差分析 - 基本公式 (Repeated Measures ANOVA - Basic Formulas)

我们将在公式中使用以下符号：

\(n\) 表示受试者 (subjects) 的数量；
\(k\) 表示变量 (variables) 的数量；
\(Xij\) 表示受试者 \(i\) 在变量 \(j\) 上的得分 (score)；
\(Xi.\) 表示受试者 \(i\) 的均值 (mean)；
\(X.j\) 表示变量 \(j\) 的均值 (mean)；
\(X..\) 表示总均值 (grand mean)。

现在，平方和 (sums of squares)，自由度 (degrees of freedom) 和均方 (mean squares) 的公式是

\[SS_{within} = \sum_{i=1}^n\sum_{j=1}^k(Xij - Xi.)^2\]

\[SS_{model} = n \sum_{j=1}^k(X.j - X..)^2\]

\[SS_{error} = SS_{within} - SS_{model}\]

\[df_{model} = k - 1\]

\[df_{error} = (k - 1)\cdot(n - 1)\]

\[MS_{model} = \frac{SS_{model}}{df_{model}}\]

\[MS_{error} = \frac{SS_{error}}{df_{error}}\]

\[F = \frac{MS_{model}}{MS_{error}}\]

重复测量方差分析 - 案例 (Repeated Measures ANOVA - Example)

我们让 10 个人执行了 4 个记忆任务。收集到的数据如下表所示。我们想知道所有四个任务的总体平均分是否相等。

受试者 (Subject)	任务 1 (task1)	任务 2 (task2)	任务 3 (task3)	任务 4 (task4)	受试者均值 (Subject Mean)
1	8	7	6	7	7
2	5	8	5	6	6
3	6	5	3	4	4.5
4	6	6	7	3	5.5
5	8	10	8	6	8
6	6	5	6	3	5
7	6	5	2	3	4
8	9	9	9	6	8.25
9	5	4	3	7	4.75
10	7	6	6	5	6
变量均值 (Variable Mean)	6.6	6.5	5.5	5	5.9 (总均值 grand mean)

如果我们应用我们的公式 (formulas) 到我们的示例数据，我们将得到

\[SS_{within} = (8 - 7)^2 + (7 - 7)^2 + ... + (5 - 6)^2 = 63.5\]

\[SS_{model} = 10 \cdot((6.6 - 5.9)^2 + (6.5 - 5.9)^2 + (5.5 - 5.9)^2 + (5 - 5.9)^2) = 18.2\]

\[SS_{error} = 63.5 - 18.2 = 45.3\]

\[MS_{model} = \frac{18.2}{3} = 6.07\]

\[MS_{error} = \frac{45.3}{27} = 1.68\]

\[F = \frac{6.07}{1.68} = 3.62\]

\[P(F(3,27) > 3.62) \approx 0.026\]

当 p < 0.05 时，通常会拒绝零假设。结论：总体均值可能最终并不相等。

重复测量方差分析 - 软件 (Repeated Measures ANOVA - Software)

我们已经在这个 Googlesheet 中计算了整个例子，如下图所示。所有读者都可以访问它，所以请随意查看我们使用的公式。

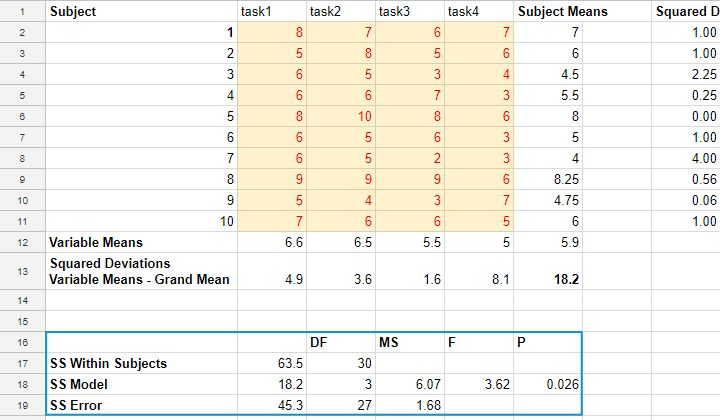
虽然你可以在 Googlesheet 中运行此测试，但你可能希望使用更专业的软件来运行重复测量方差分析。除非你安装了高级统计选项，否则默认情况下 SPSS (SPSS) 中 不包含 此测试。一个优秀的 SPSS 中重复测量方差分析的例子是 SPSS 重复测量方差分析 (SPSS Repeated Measures ANOVA)。

下图显示了我们在本教程中运行的示例的 SPSS 输出。

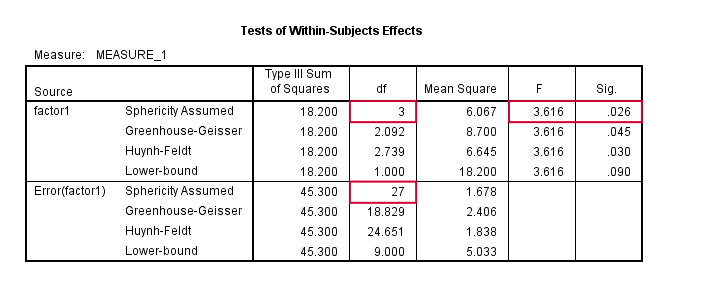
析因重复测量方差分析 (Factorial Repeated Measures ANOVA)

到目前为止，我们的讨论仅限于具有单个受试者内因子 (within-subjects factor) 的单因素重复测量方差分析 (one-way repeated measures ANOVA)。我们可以很容易地将其扩展为具有一个受试者内因子和一个受试者间因子 (between-subjects factor) 的析因重复测量方差分析。基本思想如下所示。有关 SPSS 中的一个很好的例子，请参见 SPSS 重复测量方差分析 - 示例 2 (SPSS Repeated Measures ANOVA - Example 2)。

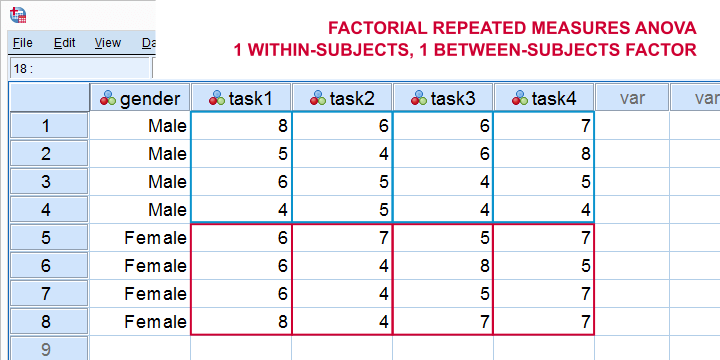
或者，我们可以将我们的模型扩展为具有 2 个受试者内因子 (within-subjects factors) 的析因重复测量方差分析。下图说明了基本思想。

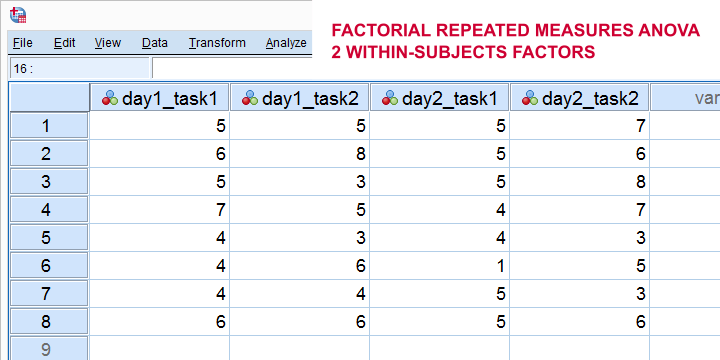
最后，我们可以将我们的模型进一步扩展为 3(+) 因素重复测量方差分析 (3(+) way repeated measures ANOVA)。（如果我们的模型包含 至少 1 个受试者内因子，我们就说“重复测量方差分析”）。