效应量:快速指南
作者:Ruben Geert van den Berg,发表于 基础知识 & 统计 A-Z
效应量(Effect Size)是一个可解释的数值,它量化了数据与某个假设之间的差异。
统计显著性 (Statistical significance) 大致是指在某个假设为真的前提下,找到当前数据的概率。如果这个概率很低,那么这个假设很可能是不成立的。这可能是一个很好的初步判断,但我们真正需要知道的是数据与假设之间 差异有多大?效应量指标用一个可解释的数值来概括这个答案。这非常重要,因为:
- 效应量允许我们比较效应——无论是在同一研究内部还是跨研究之间;
- 我们需要一个效应量指标来估计 (1 - β) 或 功效 (Power)。功效是指在某个备择假设成立的前提下,拒绝某个零假设的概率;
- 甚至在收集任何数据之前,效应量就能告诉我们需要多大的样本量 (Sample Size) 才能获得给定的功效水平——通常为 0.80。
效应量指标概览
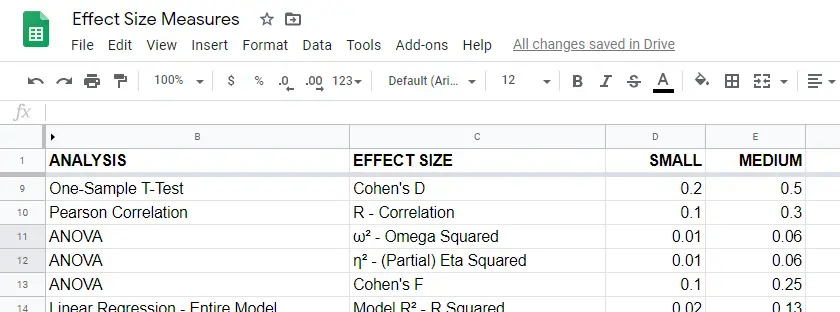
有关效应量指标的概览,请参考 这个 Google 表格,如下所示。此 Google 表格为只读模式,但可以下载并共享为 Excel 文件,以便进行排序、筛选和编辑。
卡方检验
卡方检验常用的效应量指标包括:
- Cohen’s W(适用于所有卡方检验);
- Cramér’s V (适用于卡方独立性检验)以及
- 列联系数(适用于卡方独立性检验)。
卡方检验 - Cohen’s W
Cohen’s W 是以下检验的首选效应量指标:
Cohen’s W 的基本经验法则 8:
- 小效应:w = 0.10;
- 中等效应:w = 0.30;
- 大效应:w = 0.50。
Cohen’s W 的计算公式为:
\[W = \sqrt{\sum_{i = 1}^m\frac{(P_{oi} - P_{ei})^2}{P_{ei}}}\]
其中:
- \(P_{oi}\) 表示观察到的比例;
- \(P_{ei}\) 表示在零假设下期望的比例;
- \(m\) 表示单元格的数量。
对于列联表,Cohen’s W 也可以从列联系数 \(C\) 计算得出:
\[W = \sqrt{\frac{C^2}{1 - C^2}}\]
对于列联表,第三种选择是从 Cramér’s V 计算 Cohen’s W:
\[W = V \sqrt{d_{min} - 1}\]
其中:
- \(V\) 表示 Cramér’s V;
- \(d_{min}\) 表示表格的最小维度——行数或列数。
据我们所知,没有任何统计软件包提供 Cohen’s W 的计算功能。对于列联表 (Contingency Tables),我们建议从上述列联系数计算得出。
对于频率分布的卡方拟合优度检验 (Goodness-of-fit tests),最好的选择可能是在某个电子表格编辑器中手动计算。此 Google 表格 中提供了一个计算示例。
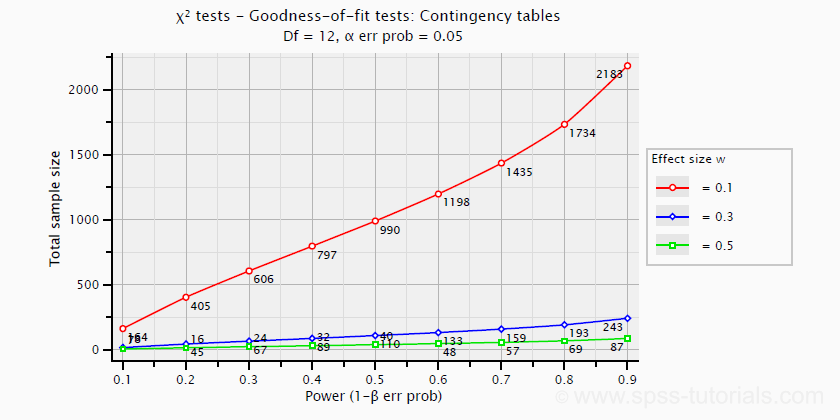
卡方检验的功效 (Power) 和所需的样本量不能直接从 Cohen’s W 计算得出:它们取决于检验的 df——自由度 (degrees of freedom) 的缩写。下面的示例图表适用于 5 · 4 表格,因此 df = (5 - 1) · (4 -1) = 12。
T 检验
T 检验常用的效应量指标包括:
- Cohen’s D(适用于所有 T 检验)以及
- 点二列相关(仅适用于 独立样本 T 检验 (Independent Samples T-Test))。
T 检验 - Cohen’s D
Cohen’s D 是所有 3 种 T 检验的首选效应量指标:
- 独立样本 T 检验 (Independent Samples T-Test)、
- 配对样本 T 检验 (Paired Samples T-Test) 以及
- 单样本 T 检验 (One Sample T-Test)。
基本的经验法则 8:
- |d| = 0.20 表示 小 效应;
- |d| = 0.50 表示 中等 效应;
- |d| = 0.80 表示 大 效应。
对于独立样本 T 检验 (Independent-Samples T-Test),Cohen’s D 的计算公式为:
\[D = \frac{M_1 - M_2}{S_p}\]
其中:
- \(M_1\) 和 \(M_2\) 表示第 1 组和第 2 组的样本均值;
- \(S_p\) 表示合并估计的总体标准差。
配对样本 T 检验 (Paired-Samples T-Test) 在技术上是对差值分数的 单样本 T 检验 (One-Sample T-Test)。对于此检验,Cohen’s D 的计算公式为:
\[D = \frac{M - \mu_0}{S}\]
其中:
- \(M\) 表示样本均值;
- \(_0\) 表示假设的总体均值(差异);
- \(S\) 表示估计的总体标准差。
JASP 以及 SPSS(27 及更高版本)中提供了 Cohen’s D 的计算功能。有关详细教程,请参考 Cohen’s D - T 检验的效应量。
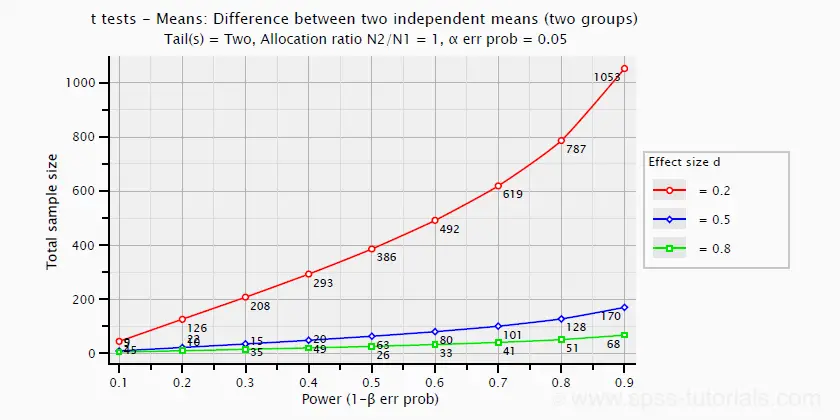
下图显示了功效和所需的总样本量与 Cohen’s D 之间的关系。它适用于两个样本量相等的独立样本 T 检验。
Pearson 相关
对于 Pearson 相关 (Pearson Correlation),相关系数本身(通常表示为 r)可以解释为效应量指标。基本的经验法则 8:
- r = 0.10 表示小效应;
- r = 0.30 表示中等效应;
- r = 0.50 表示大效应。
所有统计软件包和电子表格编辑器(包括 Excel 和 Google 表格)都提供 Pearson 相关系数的计算功能。
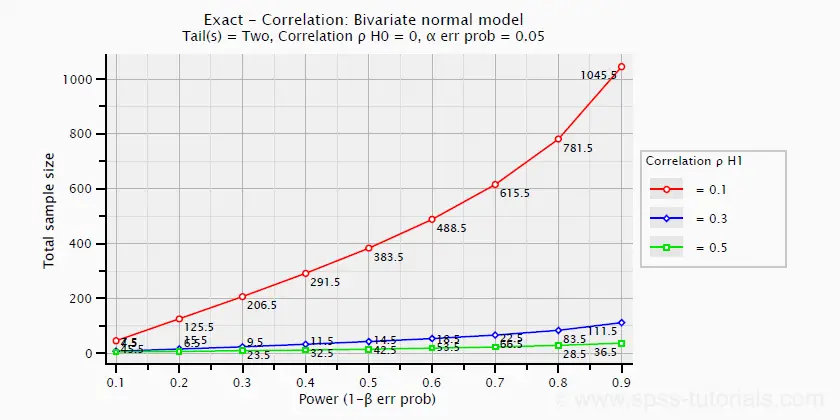
下图(在 G*Power 中创建)显示了所需的样本量和功效与效应量之间的关系。
方差分析 (ANOVA)
方差分析 (ANOVA) 常用的效应量指标包括:
- \(\) 或(偏)eta 平方;
- Cohen’s F;
- \(\) 或 omega 平方。
方差分析 - (偏)Eta 平方
偏 eta 平方(表示为 η2)是以下检验的首选效应量:
- 方差分析 (ANOVA)(被试间、单因素或析因);
- 重复测量方差分析 (Repeated Measures ANOVA)(单因素或析因);
- 混合方差分析。
基本的经验法则:
- η2 = 0.01 表示小效应;
- η2 = 0.06 表示中等效应;
- η2 = 0.14 表示大效应。
偏 eta 平方的计算公式为:
\[\eta^2_p = \frac{SS_{effect}}{SS_{effect} + SS_{error}}\]
其中:
- \(^2_p\) 表示偏 eta 平方;
- \(SS\) 表示效应和误差的平方和。
此公式也适用于单因素方差分析,在这种情况下,偏 eta 平方等于 eta 平方。
我们所知的所有统计软件包(包括 JASP 和 SPSS)都提供偏 eta 平方的计算功能。有关后者,请参阅 如何从 SPSS 获取(偏)Eta 平方?
方差分析 - Cohen’s F
Cohen’s f 是以下检验的效应量指标:
- 方差分析 (ANOVA)(被试间、单因素或析因);
- 重复测量方差分析 (Repeated Measures ANOVA)(单因素或析因);
- 混合方差分析。
Cohen’s f 的计算公式为:
\[f = \sqrt{\frac{\eta^2_p}{1 - \eta^2_p}}\]
其中 \(^2_p\) 表示(偏)eta 平方。
Cohen’s f 的基本经验法则 8:
- f = 0.10 表示小效应;
- f = 0.25 表示中等效应;
- f = 0.40 表示大效应。
G*Power 从各种其他指标计算 Cohen’s f。我们不知道有任何其他软件包可以计算 Cohen’s f。
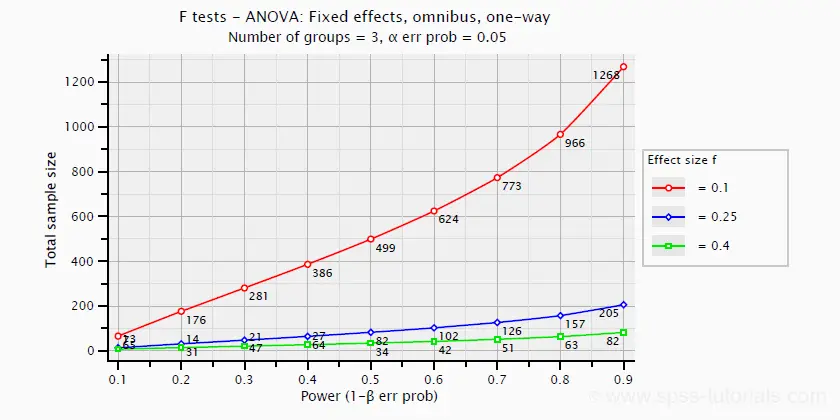
方差分析的功效和所需的样本量可以从 Cohen’s f 和其他一些参数计算得出。下面的示例图表显示了所需的样本量与小、中、大效应的功效之间的关系。它适用于 3 个大小相等的组的单因素方差分析。
方差分析 - Omega 平方
\(^2\) 或 Omega 平方是(偏)eta 平方的一种不太常见但更好的替代方案,其计算公式为:
\[\omega^2 = \frac{SS_{effect} - df_{effect}\cdot MS_{error}}{SS_{total} + MS_{error}}\]
其中:
- \(SS\) 表示平方和;
- \(df\) 表示自由度;
- \(MS\) 表示均方。
与(偏)eta 平方类似,\(^2\) 估计结果变量中由整个总体中的效应解释的方差比例。然而,后者是一个偏差较小的估计量。1, 2, 6 基本经验法则 5:
- 小效应:ω2 = 0.01;
- 中等效应:ω2 = 0.06;
- 大效应:ω2 = 0.14。
SPSS 27 及更高版本中提供了 \(^2\) 的计算功能,但前提是您从 分析 (Analyze)  比较平均值 (Compare Means)
比较平均值 (Compare Means)  单因素方差分析 (One-Way ANOVA) 运行方差分析。SPSS 中的其他方差分析选项(通过一般线性模型或平均值)尚未包含 \(^2\)。但是,通过将标准方差分析表复制到 Excel 并手动输入公式,也可以非常容易地计算出来。
单因素方差分析 (One-Way ANOVA) 运行方差分析。SPSS 中的其他方差分析选项(通过一般线性模型或平均值)尚未包含 \(^2\)。但是,通过将标准方差分析表复制到 Excel 并手动输入公式,也可以非常容易地计算出来。
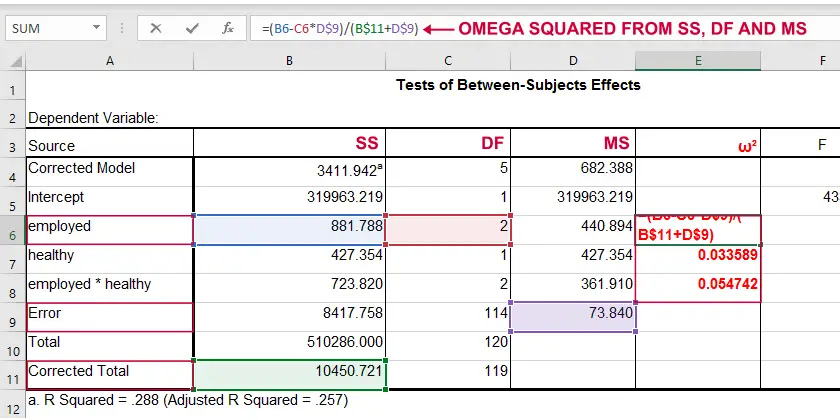 注意:您需要“校正总数”才能从 SPSS 输出计算 omega 平方。
注意:您需要“校正总数”才能从 SPSS 输出计算 omega 平方。
线性回归
(简单和多元)线性回归的效应量指标包括:
- \(\)(整个模型和单个预测变量);
- \(R^2\)(整个模型);
- \(r_{part}^2\) - 平方半偏相关(或“部分”)相关(单个预测变量)。
线性回归 - F 平方
(简单和多元)线性回归的首选效应量指标是 \(f^2\)。基本的经验法则 8:
- \(f^2\) = 0.02 表示小效应;
- \(f^2\) = 0.15 表示中等效应;
- \(f^2\) = 0.35 表示大效应。
\(f^2\) 的计算公式为:
\[f^2 = \frac{R_{inc}^2}{1 - R_{inc}^2}\]
其中 \(R_{inc}^2\) 表示一组预测变量相对于另一组预测变量的 r 平方增加量。整个多元回归模型和单个预测变量都是此通用公式的特例。
对于整个模型 (Entire Model),\(R_{inc}^2\) 是模型中预测变量相对于空预测变量集的 r 平方增加量。在没有任何预测变量的情况下,我们估计每个观察值的因变量总平均值,并且我们有 \(R^2 = 0\)。在这种情况下,\(R_{inc}^2 = R^2_{model} - 0 = R^2_{model}\) - 多元回归模型的“正常” r 平方。
对于单个预测变量 (Individual Predictor),\(R_{inc}^2\) 是将此预测变量添加到模型中已有的其他预测变量所产生的 r 平方增加量。它等于 \(r^2_{part}\) - 某个预测变量的平方半偏(或“部分”)相关。这使得在 Excel 中计算单个预测变量的 \(f^2\) 非常容易,如下所示。
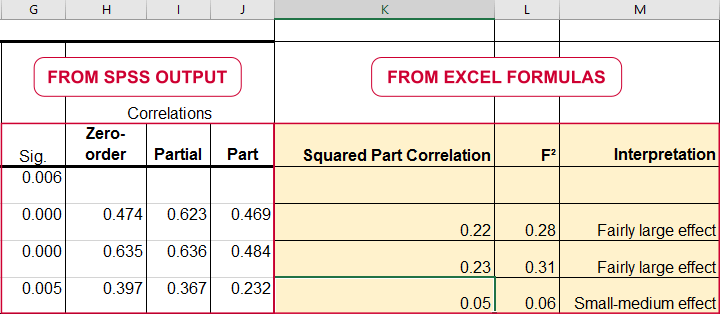
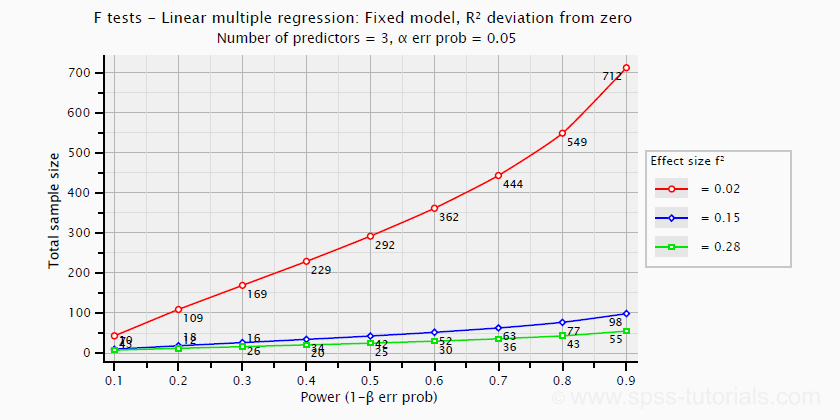
\(f^2\) 可用于计算回归模型或单个预测变量的功效和/或所需的样本量。但是,这些也取决于所涉及的预测变量的数量。下图显示了具有 3 个预测变量的多元回归模型所需的样本量如何取决于所需的功效和估计的(总体)效应量。
参考文献
- Van den Brink, W.P. & Koele, P. (2002). Statistiek, deel 3 [统计,第 3 部分]。阿姆斯特丹:Boom。
- Warner, R.M. (2013). 应用统计学(第 2 版)。千橡市,加利福尼亚州:SAGE。
- Agresti, A. & Franklin, C. (2014). 统计学。从数据中学习的艺术与科学。 埃塞克斯:Pearson Education Limited。
- Hair, J.F., Black, W.C., Babin, B.J. et al (2006). 多元数据分析。 新泽西州:Pearson Prentice Hall。
- Field, A. (2013). 使用 IBM SPSS 统计信息发现统计信息。纽伯里公园,加利福尼亚州:Sage。
- Howell, D.C. (2002). 心理统计方法(第 5 版)。太平洋格罗夫,加利福尼亚州:Duxbury。
- Siegel, S. & Castellan, N.J. (1989). 行为科学的非参数统计(第 2 版)。新加坡:McGraw-Hill。
- Cohen, J (1988). 社会科学的统计功效分析(第 2 版)。希尔斯代尔,新泽西州,劳伦斯·埃尔鲍姆协会。
- Pituch, K.A. & Stevens, J.P. (2016). 社会科学的应用多元统计(第 6 版)。纽约:Routledge。