SPSS 符号检验：比较两个中位数 - 简单示例
By Ruben Geert van den Berg under Statistics A-Z & Nonparametric Tests 
符号检验 (Sign Test) 用于评估在同一组案例上测量的两个变量是否可能具有相等的总体中位数 (population medians)。 还有一种符号检验用于将一个中位数与理论值进行比较，它与我们将在此讨论的检验非常相似。另请参阅 SPSS 符号检验：比较一个中位数 - 简单示例。 符号检验可以用于度量变量 (metric variables) 或顺序变量 (ordinal variables)。 如果要比较均值而不是中位数，则 配对样本 t 检验 (paired samples t-test) 和 Wilcoxon 符号秩检验 (Wilcoxon signed-ranks test) 是更好的选择。
广告评分数据 (Adratings Data)
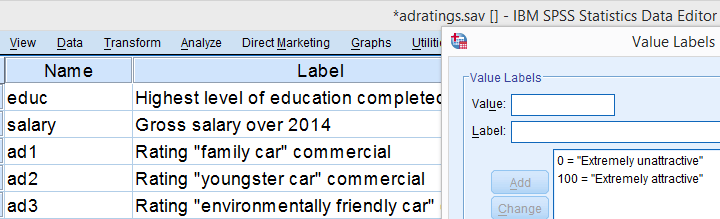
在本教程中，我们将使用 adratings.sav 数据集。它包含 18 名受访者对 3 个汽车广告的吸引力评分数据。 其变量字典 (dictionary) 的一部分如下所示。
描述性统计 (Descriptive Statistics)
每当你开始处理数据时，始终从快速 数据检查 (data check) 开始，并且仅在你的数据看起来合理时才继续。 adratings 数据看起来不错，所以我们将继续进行一些描述性统计。 我们将使用 MEANS 来检查 3 个评分变量的中位数，方法是运行以下语法 (syntax)。DESCRIPTIVES 似乎是更自然的选择，但奇怪的是，它不包含中位数，即使这些显然是“描述性统计”。
用于检查中位数的 SPSS 语法 (Syntax)
***Run descriptive statistics with medians in nice table.
**
means ad1 to ad3
/cells count mean median.SPSS 中位数输出 (Output)
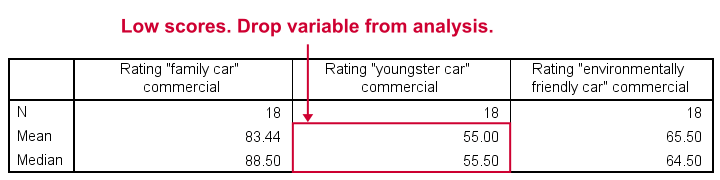
第二个广告（“Youngster Car”）的平均值和中位数评分非常低。 因此，我们将从进一步的分析中排除此变量，并将重点放在第一个和第三个广告上。
符号检验 - 零假设 (Null Hypothesis)
出于某种原因，我们的营销经理只对比较中位数评分感兴趣，因此我们的零假设 (null hypothesis) 是： 对于我们的 2 个评分变量，两个总体中位数 (population medians) 相等。 我们将通过创建一个包含符号的新变量来检查这一点：
- 评价 ad1 < ad3 的受访者得到一个 负号 (minus sign) ；
- 评价 ad1 > ad3 的受访者得到一个 正号 (plus sign) 。
如果我们的零假设为真，那么正号和负号应该大致在我们的样本中 50/50 分布。 在 H0 下，非常 不同的分布不太可能出现，因此表明总体中位数可能根本不相等。
在 SPSS 中运行符号检验
运行符号检验最直接的方法如下面的屏幕截图所示。
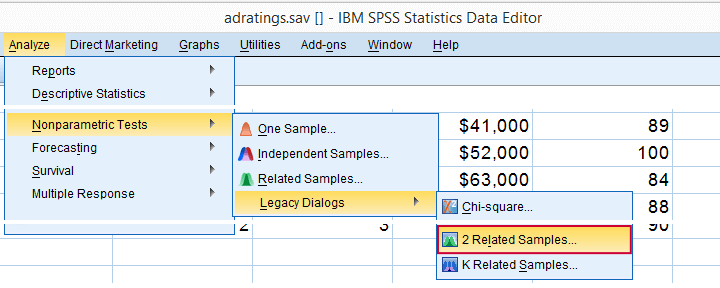
“2 Re l ated samples” 指的是我们正在测试的两个评分变量。 它们是相关的（而不是独立的），因为它们是在同一受访者身上测量的。
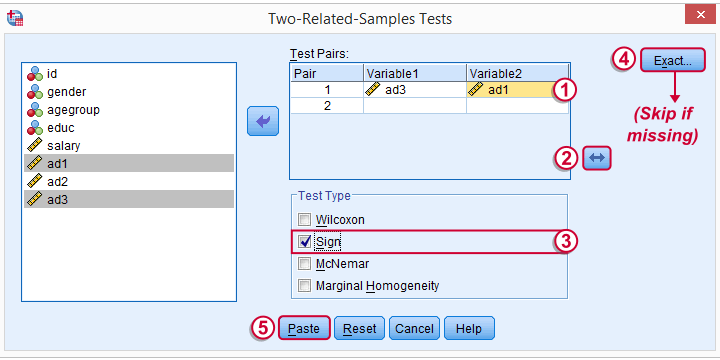
我们更喜欢将评分最高的变量放在第二个位置。 我们将通过反转变量顺序来实现这一点。 
你的菜单是否包含“E x act”按钮取决于你的 SPSS 许可证。 如果它不存在，只需跳过下面显示的步骤。
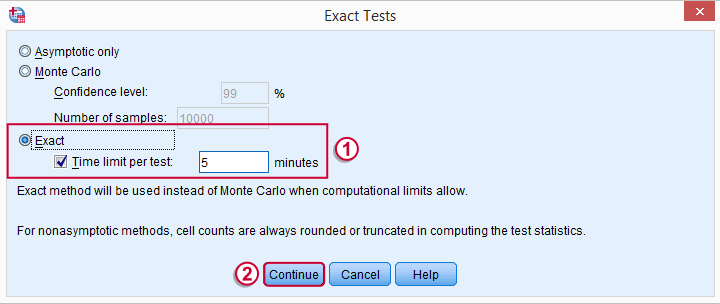
SPSS 符号检验语法 (Syntax)
完成这些步骤将生成以下语法（如果包含精确检验 (exact test)，你将有一行额外的代码）。 让我们运行它。
***Sign test for 2 related medians syntax.
**
NPAR TESTS
/SIGN=ad3 WITH ad1 (PAIRED)
/MISSING ANALYSIS.输出 - 符号表 (Signs Table)
首先，结 (ties)（即：两个变量得分相同的受访者）完全从该分析中排除。 这对于典型的李克特量表 (Likert scales) 来说可能是一个问题。 幸运的是，我们变量的百分比量表使这种情况发生的可能性大大降低。 由于我们有 18 名受访者，我们的零假设表明其中大约 9 名应该认为 ad1 比 ad3 更高。 结果发现，有 12 个案例而不是 9 个案例成立。 我们能否合理地期望仅通过从某个大型总体中随机抽样 18 个案例而获得这种差异？
输出 - 检验统计量表 (Test Statistics Table)
Exact Sig. (2-tailed) 指的是我们的 p 值 (p-value)，值为 0.24。 这意味着如果我们的零假设为真，则有 24% 的机会发现观察到的差异。 我们的发现并不与我们的假设（总体中位数相等）相矛盾。 在许多情况下，输出将包括 “Asymp. Sig. (2-tailed)”，这是一个基于 标准正态分布 (standard normal distribution) 的近似 p 值。 SPSS 省略了计算 Z 的连续性校正 (continuity correction)，这会将 p 值（略微）偏向于零。 现在不包括它，因为我们的样本量 n <= 25。
报告我们的符号检验结果
在报告符号检验时，请包括显示符号和（可能）结的整个表格。 尽管可以很容易地从中计算出 p 值，但我们将添加类似“符号检验没有显示两个中位数之间的任何差异，精确二项式 p (2-tailed) = 0.24。”的内容。
更多关于 P 值
基本上就是这样了。 但是，对于那些好奇的人，我们现在将进行更详细的介绍。 首先是 p 值。 在我们的 18 个案例中，0 到 18 个案例可能有一个正号（即：ad1 的评分高于 ad3）。 我们的零假设规定每个案例有 0.5 的可能性这样做，这就是为什么正号的数量遵循二项式 抽样分布 (sampling distribution)，如下所示。
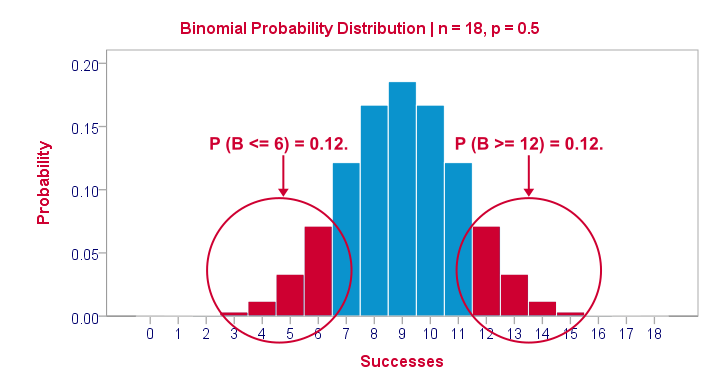
最可能的结果是 9 个正号，概率约为 0.175：如果我们抽取 1,000 个随机样本而不是 1 个样本，我们预计其中约 175 个样本会产生 9 个正号。 大约 12% 的样本应该产生 6 个或更少的正号，或者 12 个或更多的正号。 报告 双尾 p 值 (2-tailed p-value) 会考虑两个尾部（红色区域），因此会产生 p = 0.24，就像我们在输出中看到的那样。
没有符号检验的 SPSS 符号检验
此时，你可能会看到符号检验实际上等同于对包含我们符号的变量进行 二项式检验 (binomial test)。 如果你想要精确的 p 值，但你的输出中只有近似的 p 值 “Asymp. Sig. (2-tailed)”，这可能会派上用场。 我们的最后一个语法示例展示了如何以两种不同的方式完成它。
精确 P 值的解决方法
***Compute plusses and minuses.
**
if(ad1 > ad3) sign = 1.
if(ad3 > ad1) sign = 0.
value labels sign 0 '- (minus)' 1 '+ (plus)'.
***Option 1: binomial test.
**
NPAR TESTS
/BINOMIAL (0.50)=sign
/MISSING ANALYSIS.
***Option 2: compute p manually.
**
frequencies sign.
***Compute p-value manually. It is twice the probability of flipping 6 or
fewer heads when flipping a balanced coin 18 times.
**
compute pvalue = 2 * cdf.binom(6,18,0.5).
execute.