SPSS 层次回归教程

作者：Ruben Geert van den Berg，分类：回归分析

层次回归（Hierarchical Regression）旨在比较不同的回归模型。每个模型在前一个模型的基础上增加一个或多个预测变量，从而形成一个模型的“层次结构”。在 SPSS 中进行这种分析非常简单，但我们需要注意一些回归分析的假设前提：

• 线性性 (Linearity)：每个预测变量与结果变量之间存在线性关系；
• 正态性 (Normality)：预测误差在总体中呈正态分布；
• 同方差性 (Homoscedasticity)：误差的方差在总体中是恒定的。

此外，让我们首先确保我们的数据有意义，并选择我们将包含在模型中的预测变量。下面的步骤总结了这些步骤。

SPSS 层次回归步骤

步骤	原因	操作
1	检查直方图	查看分布是否合理。
2	检查描述性统计	查看是否有任何变量的 N 值较低。检查 Listwise 有效 N。
3	检查散点图	查看关系是否是线性的。寻找有影响力的案例。
4	检查相关矩阵	查看 Pearson 相关系数是否合理。
5	回归 I：模型选择	查看哪个模型是好的。
6	回归 II：残差	检查残差图。

案例研究 - 员工满意度

一家公司进行了一项员工满意度调查，其中包括总体员工满意度。员工还对一些主要的职位质量方面进行了评分，结果保存在 work.sav 文件中。

SPSS 多元回归教程 变量视图

我们想要回答的主要问题是：哪些质量方面可以预测工作满意度？让我们按照我们的步骤来找出答案。

检查所有直方图

首先，让我们看看我们的数据是否合理。我们将通过对所有预测变量和因变量运行直方图来实现这一点。最简单的方法是运行下面的语法。有关更详细的说明，请参阅 在 SPSS 中创建直方图。

***检查结果变量和所有预测变量的直方图。**
frequencies overall to tasks
/format notable
/histogram.

结果

SPSS 多元回归教程 直方图 结果变量

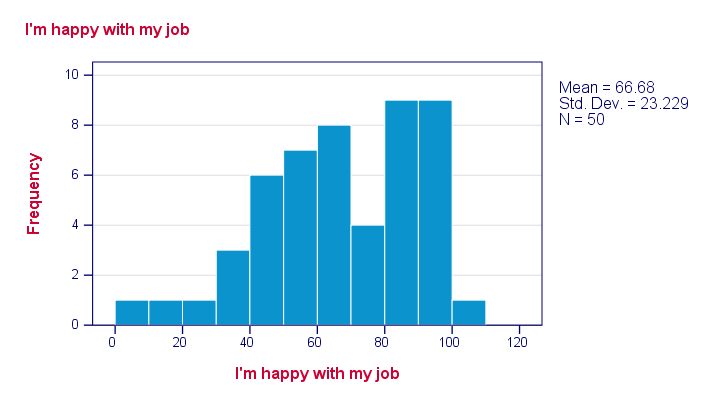
简单地查看我们的 6 个直方图告诉我们：

• 这些变量都不包含任何系统缺失值 (System Missing Values)；
• 我们的变量都不包含任何明显的异常值 (Outliers)：无需设置任何用户缺失值 (User Missing Values)；
• 所有频率分布看起来都是合理的。

如果直方图_确实_显示了不太可能的值，那么在进行分析之前，必须将这些值设置为 用户缺失值 (User Missing Values)。

检查描述性统计表

如果变量包含缺失值，则简单的描述性统计表是检查缺失程度的快速方法。我们将从单行 语法 (Syntax) 中运行它。

***检查描述性统计。**
descriptives overall to tasks.

结果

SPSS 多元回归教程 描述性统计

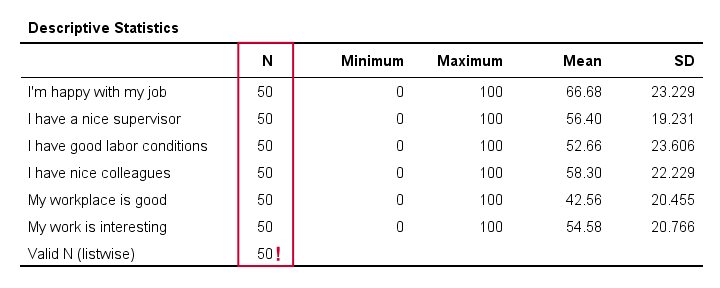
描述性统计表告诉我们是否有任何变量具有许多缺失值。如果是这样，您可能需要从分析中排除这些变量。

有效 N (Listwise) 是指在该表中任何变量上都没有缺失值的案例数。除非您选择成对删除缺失值（我们稍后会看到），否则 SPSS 回归（以及因子分析 (Factor Analysis)）仅使用此类完整案例。

检查散点图

我们的预测变量与结果变量之间是否具有（大致）线性关系？大多数教科书建议检查残差图：预测值（x 轴）与残差（y 轴）的散点图 (Scatterplots)应该能够检测到非线性。

但是，我认为残差图对于检查线性是无用的。原因是预测值是预测变量的（加权）组合。那么，如果只有一个预测变量与结果变量之间存在曲线关系呢？这种曲线关系会被预测变量组合成一个变量（预测值）而稀释。

分别检查每个预测变量的线性更有意义。一种最简单的方法是为每个预测变量（x 轴）与结果变量（y 轴）运行散点图。

创建这些散点图的简单方法是 粘贴 (Paste) 从菜单中粘贴一个命令，如 SPSS 散点图教程 中所示。接下来，删除换行符并根据需要复制粘贴编辑它。

***检查所有预测变量（x 轴）与结果变量（y 轴）的散点图。**
GRAPH /SCATTERPLOT(BIVAR)= supervisor WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= conditions WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= colleagues WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= workplace WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= tasks WITH overall /MISSING=LISTWISE.

结果

SPSS 多元回归教程 散点图

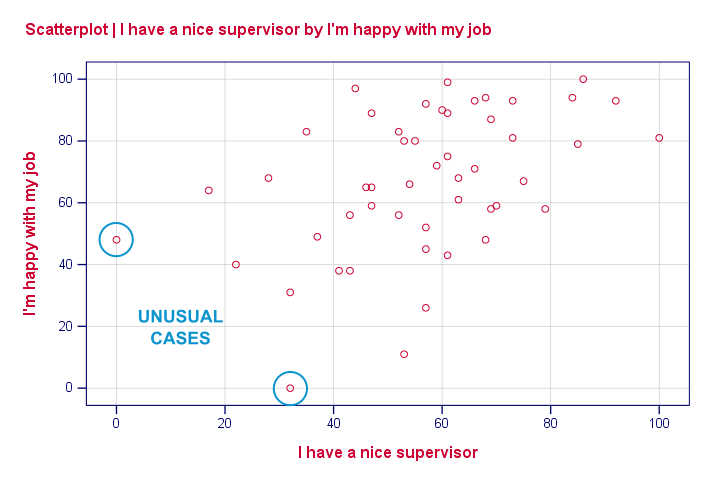
我们的散点图都没有显示出明显的曲线关系。但是，我们确实看到了一些不符合点整体模式的异常案例。我们将使用下面的语法标记和检查这些案例。

***标记具有（总体满意度 > 40）和（主管 < 10）的异常案例。**
compute flag1 = (overall > 40 and supervisor < 10).

***将异常案例移动到文件顶部以进行目视检查。**
sort cases by flag1(d).

结果

SPSS 多元回归 异常案例 数据视图

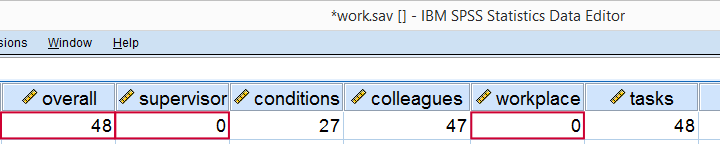
我们的第一个案例看起来确实很奇怪：主管和工作场所都是 0（不能更糟了），但总体工作评价却非常好。我们或许应该使用 FILTER 将这些案例从进一步的分析中排除，但我们现在暂时忽略它们。

关于线性，我们的散点图提供了一个最简单的检查。一个更好的方法是检查线性和非线性拟合线，如 如何在 SPSS 中绘制回归线？ 中所述。

一个非常快速和容易地做到这一点的极好工具可以从 SPSS - 创建所有散点图工具 下载。

SPSS 散点图拟合线工具 840

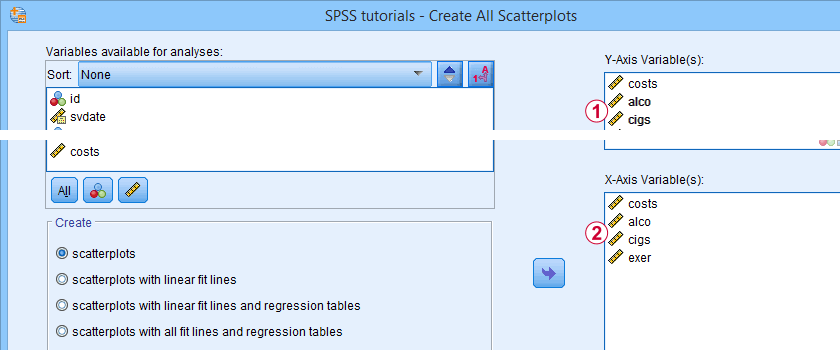
检查相关矩阵

我们现在将看看所有变量之间的 (Pearson) 相关性是否合理。对于手头的数据，我预计只有正相关，例如，大约在 0.3 到 0.7 之间。有关更多详细信息，请阅读 SPSS 相关分析。

***检查相关矩阵是否合理。**
correlations overall to tasks
/print nosig
/missing pairwise.

结果

SPSS 多元回归教程 相关矩阵

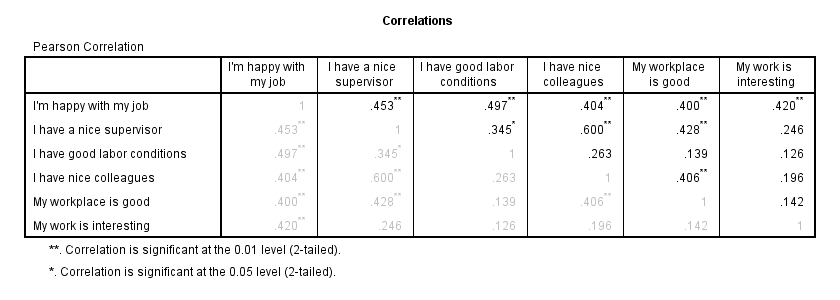
相关性的模式看起来完全合理。像这样创建一个漂亮而干净的相关矩阵在 SPSS 相关性 APA 格式 中进行了介绍。

回归 I - 模型选择

我们接下来想要回答的问题是：哪些预测变量对预测工作满意度有实质性贡献？ 我们的相关性显示，所有预测变量都与结果变量 具有统计显着性 相关。 但是，预测变量本身之间也存在实质性相关性。 也就是说，它们重叠。

由预测变量解释的工作满意度中的某些方差也可能由其他一些预测变量解释。 如果是这样，则此其他预测变量可能不会对我们的预测做出_独特_的贡献。

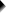有不同的方法来寻找正确的预测变量选择。 其中一种方法是将所有预测变量逐个添加到回归方程中。 由于我们有 5 个预测变量，因此这将导致 5 个模型。 因此，让我们导航到 分析 (Analyze) 回归 (Regression) 线性 (Linear) 并填写如下所示的对话框。

SPSS 多元回归对话框 1

我们选择的 前进 (Forward) 方法意味着 SPSS 将添加所有 p 值小于某个选择的常数（通常为 0.05）的预测变量（一次一个）。 准确地说，这是零假设（即该预测变量的总体 b 系数为零）的 p 值。

选择 0.98（甚至更高）通常会导致所有预测变量都添加到回归方程中。

默认情况下，SPSS 仅使用预测变量和结果变量上没有缺失值的案例（“Listwise 排除”）。 如果缺失值分散在变量上，则这可能导致实际上很少的数据用于分析。 对于具有缺失值的案例，成对 (Pairwise) 排除会尝试使用所有非缺失值进行分析。 成对删除并非没有争议，有时可能会导致计算问题。

语法 回归 I - 模型选择

***回归 I：查看哪个模型看起来是正确的。**
REGRESSION
/MISSING PAIRWISE /*... 因为 LISTWISE 仅使用完整的案例 ...*/
/STATISTICS COEFF OUTS R ANOVA CHANGE
/CRITERIA=PIN(.98) POUT(.99)
/NOORIGIN
/DEPENDENT overall
/METHOD=FORWARD supervisor conditions colleagues workplace tasks.

结果 回归 I - 模型汇总

SPSS 多元回归教程 模型汇总

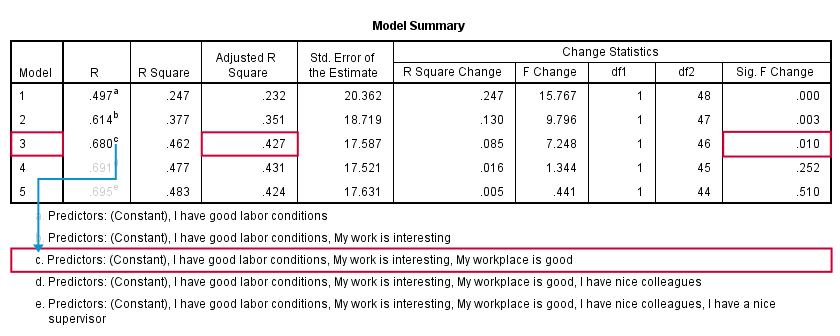
SPSS 通过一次添加一个预测变量来拟合 5 个回归模型。 模型汇总 (Model Summary) 表显示了每个模型的一些统计数据。 通过添加第三个预测变量，调整后的 R 平方 (Adjusted R-Square) 列显示它从 0.351 增加到 0.427。

但是，通过添加第四个预测变量，调整后的 R 平方几乎没有进一步增加，甚至在输入第五个预测变量时会_降低_。 在我们的模型中包含超过 3 个预测变量没有任何意义。 “Sig. F Change”列证实了这一点：从添加第三个预测变量开始，R 平方的增加具有统计显着性，F (1,46) = 7.25，p = 0.010。 添加第四个预测变量不会显着提高 R 平方。 简而言之：此表表明我们应该选择模型 3。

结果 回归 I - B 系数

SPSS 多元回归教程 系数 1

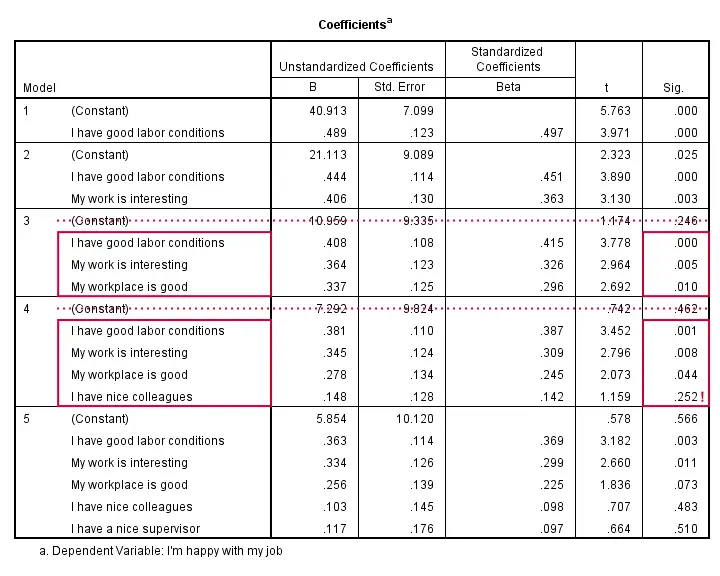
系数表显示模型 3 的所有 b 系数 均具有统计显着性。 对于第四个预测变量，p = 0.252。 其 b 系数 0.148 在统计上不显着。 也就是说，在我们的总体中它很可能为零。 实际上，我们不能认真对待 b = 0.148。 我们不应该使用它来预测工作满意度。 除了这个 N = 50 的小样本外，它不太可能恶化（而不是提高）预测准确性。

请注意，当我们添加更多预测变量时，所有 b 系数都会缩小。 如果我们包含 5 个预测变量（模型 5），则只有 2 个具有统计显着性。 如果我们估计的系数太多，则 b 系数变得不可靠。

一个经验法则是，我们需要每个预测变量 15 个观测值。 对于 N = 50，我们不应包含超过 3 个预测变量，并且系数表完全显示了这一点。 结论？ 我们选择模型 3，该模型表示满意度 = 10.96 + 0.41 * conditions + 0.36 * interesting + 0.34 * workplace。 现在，在报告此模型之前，我们应该仔细查看是否满足我们的回归假设。 我们通常通过检查回归残差图来做到这一点。

回归 II - 残差图

让我们重新打开我们的回归对话框。 一种简单的方法是使用工具栏上的对话框召回工具。 由于模型 3 排除了 supervisor 和 colleagues，因此我们将从模型中删除它们，如下所示。

SPSS 多元回归对话框 2

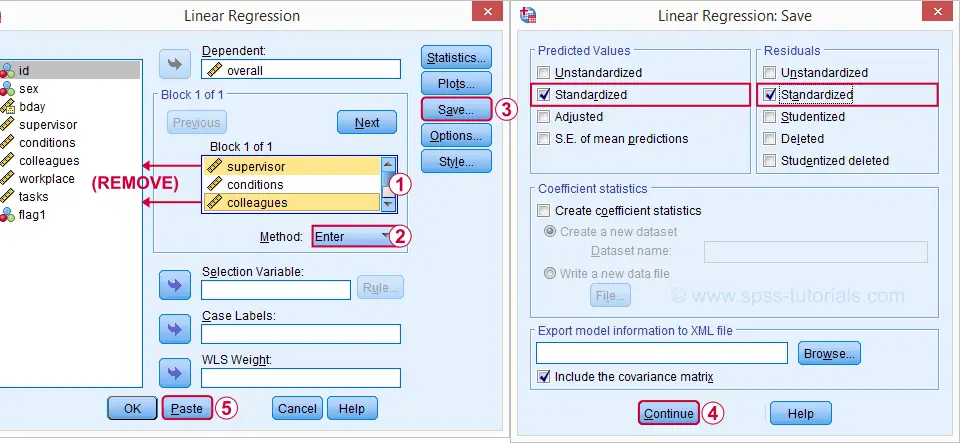
现在，回归对话框可以创建一些残差图，但我宁愿自己做。 如果我们 将预测值和残差另存为我们数据中的新变量，这很容易做到。

语法 回归 II - 残差图

***回归 II：重新拟合选择的模型并保存残差和预测值。**
REGRESSION
/MISSING PAIRWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA CHANGE /*CI(95) = B 系数的 95% 置信区间。*/
/CRITERIA=PIN(.98) POUT(.99)
/NOORIGIN
/DEPENDENT overall
/METHOD=ENTER conditions workplace tasks /*现在只有 3 个预测变量。*/
/SAVE ZPRED ZRESID.

结果 回归 II - 正态性假设

首先请注意，SPSS 向我们的数据添加了两个新变量：ZPR_1 包含我们预测值的 z 分数。 ZRE_1 是标准化残差。

SPSS 多元回归 标准化预测值 数据视图

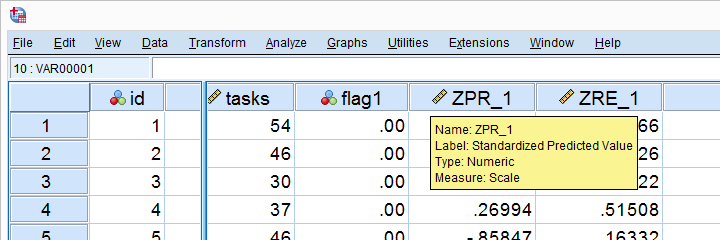
让我们首先看看残差是否 呈正态分布。 我们将通过快速直方图来做到这一点。

***直方图，用于检查残差是否呈正态分布。**
frequencies zre_1
/format notable
/histogram normal.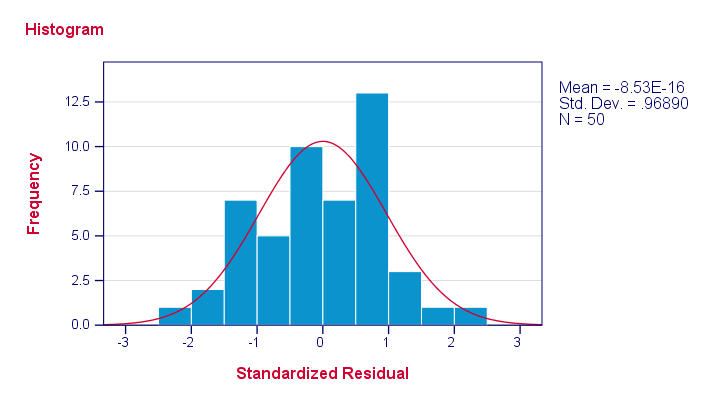

SPSS 多元回归 直方图 残差

请注意，我们的残差大致呈正态分布。

结果 回归 II - 线性性和同方差性

现在让我们看看同方差性在多大程度上成立。 我们将为我们的预测值（x 轴）创建带有残差（y 轴）的散点图。

***用于异方差和/或非线性性的散点图。**
GRAPH
/SCATTERPLOT(BIVAR)= zpr_1 WITH zre_1
/title "用于评估同方差性和线性性的散点图"。

结果

SPSS 多元回归 同方差性 线性性

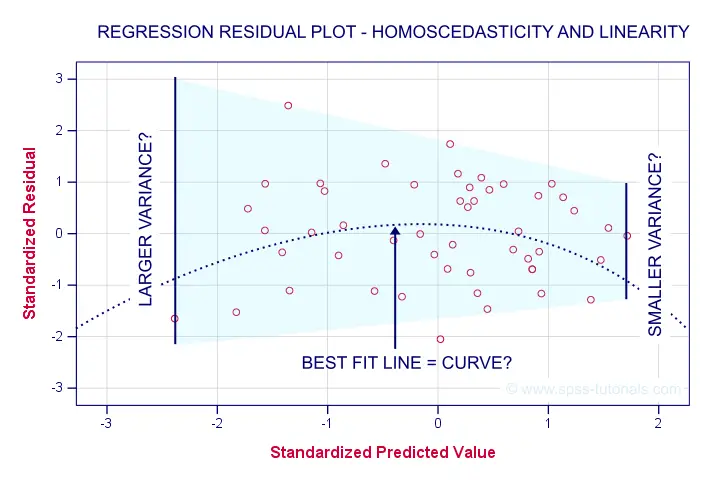
首先，当我们从左向右移动时，我们的点在垂直方向上的分散似乎较少。 也就是说：残差方差似乎随着更高的预测值而降低。 这种模式被称为 异方差性 (Heteroscedasticity)，表明 (略微) 违反了同方差性假设。

其次，我们的点似乎遵循某种 弯曲 (Curved)（而不是直线或线性 (Linear)）的模式。 尝试将一些曲线模型拟合到这些数据可能是一个明智之举，但让我们将其留到以后再讨论。

好了，现在就这样。 关于 APA 报告多元回归结果的一些指南在 SPSS 中的线性回归 - 一个简单的例子 中进行了讨论。