零假设 (Null Hypothesis) - 简明介绍

作者：Ruben Geert van den Berg，来源：统计学A-Z

零假设 (Null Hypothesis, H0) 是关于总体的精确陈述，我们试图用样本数据来拒绝它。通常，我们并不认为零假设是正确的。但是，我们需要某些确切的陈述作为统计显著性检验的起点。

零假设是统计显著性检验的起点

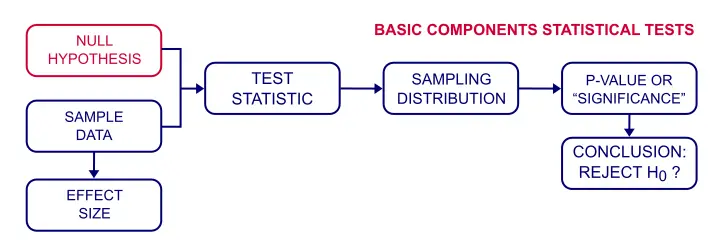
零假设的例子

通常（但并非总是），零假设声明变量或子群体之间没有关联或差异。以下是一些典型的零假设示例：

“零”不意味着“等于零”

一个常见的误解是“零 (null)”意味着“零 (zero)”。这通常但并非总是如此。例如，零假设也可以声明挫折感和攻击性之间的相关性为0.5。这里没有涉及零，并且（虽然有点不寻常）完全有效。“零假设 (null hypothesis)”中的“零 (null)”源于“无效 (nullify)”：零假设是我们试图反驳的陈述，无论它是否指定零效应。

零假设检验 - 如何运作？

我想知道在荷兰人中，幸福感是否与财富有关。找到答案的一种方法是制定一个零假设。由于“有关 (related to)”不够精确，我们选择相反的陈述作为我们的零假设：在所有荷兰人中，财富与幸福感之间的相关性为零。现在，我们将尝试反驳这个假设，以证明幸福感和财富确实有关。

现在，我们不能合理地询问所有17,142,066荷兰人他们通常的幸福感。

零假设 - 人口计数器

因此，我们将询问一个样本 (sample)（例如，100人）关于他们的财富和幸福感。结果表明，在我们的样本中，幸福感和财富之间的相关性为0.25。现在我们遇到了一个问题：样本结果往往与总体结果有所不同。因此，如果相关性 (correlation)在我们的总体中确实为零，我们可能会在样本中发现一个非零的相关性。为了说明这个重要的一点，请看下面的散点图 (scatterplot)。它可视化了N = 200的整个总体中幸福感和财富之间的零相关性。

零假设 - 人口散点图

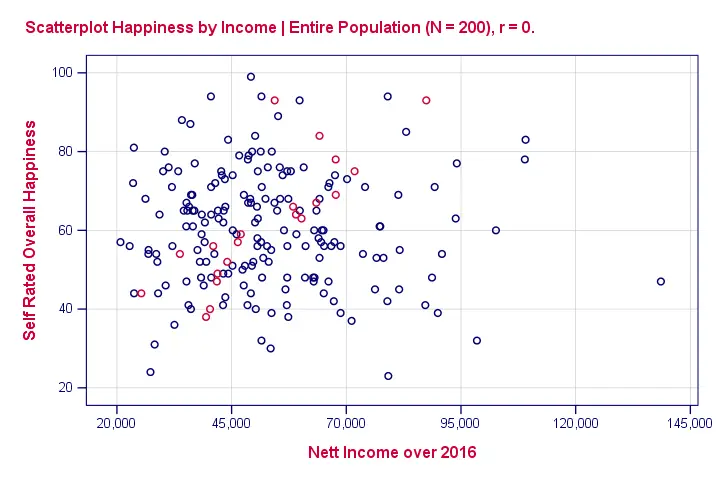
现在我们从这个总体中抽取一个N = 20的随机样本（我们之前散点图中的红点）。即使我们的总体相关性为零，我们在我们的样本中也发现了惊人的0.82的相关性。下图通过省略我们之前散点图中所有未抽样的单位来说明了这一点。

零假设 - 样本散点图

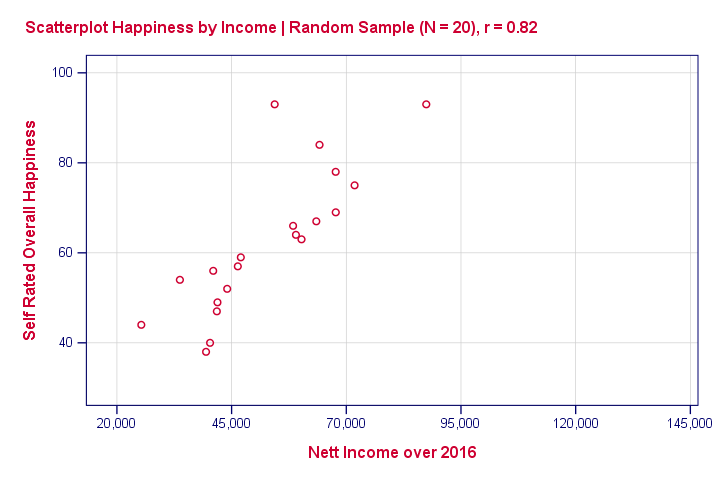
这提出了一个问题：如果我们只有来自总体的一个小样本，我们怎么能说任何关于我们总体的事情？基本的答案是：我们很少能100％确定地说任何事情。但是，我们可以以99％，95％或90％的确定性说很多。

概率 (Probability)

那么，这如何运作呢？基本上，在给定我们的零假设的情况下，某些样本结果是非常不可能的。例如，下图显示了如果总体相关性确实为零，则不同样本相关性（N = 100）的概率。

零假设 - 相关性的抽样分布

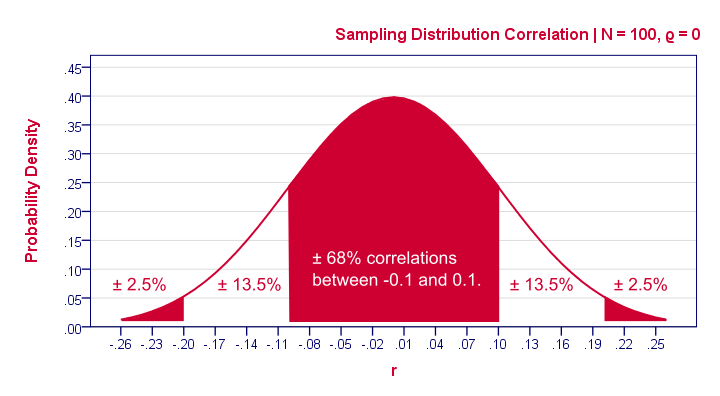
计算机可以很容易地计算出这些概率。但是，这样做需要样本量（在我们的例子中为100）和一个假定的总体相关性ρ（在我们的例子中为0）。所以这就是我们需要零假设的原因。如果我们仔细观察这个抽样分布 (sampling distribution)，我们看到0附近的样本相关性最有可能：找到-0.1和0.1之间的相关性的概率为0.68。这意味着什么？请记住，概率可以被视为相对频率。因此，假设我们抽取1,000个样本而不是我们拥有的一个样本。这将导致1,000个相关系数，其中大约680个（相对频率为0.68）将在-0.1到0.1的范围内。同样，找到-0.2和0.2之间的样本相关性的概率为0.95（或95％）。

P值 (P-Values)

我们发现样本相关性为0.25。如果总体相关性为零，这种情况发生的可能性有多大？答案被称为p值 (p-value)（概率值的缩写）：p值是在零假设为真的情况下，发现某个样本结果或更极端结果的概率。给定我们的0.25相关性，“更极端 (more extreme)”通常意味着大于0.25或小于-0.25。我们无法从我们的图表中得知，但底层表格告诉我们p≈0.012。如果零假设为真，则找到我们的样本相关性的概率为1.2％。

结论？

如果我们的总体相关性确实为零，那么我们可以在N = 100的样本中找到0.25的样本相关性。这种情况发生的概率仅为0.012，因此非常不可能。一个合理的结论是，我们的总体相关性毕竟不是零。结论：我们拒绝零假设。根据我们的样本结果，我们不再相信幸福感和财富无关。但是，我们仍然不能肯定地说这一点。

零假设 - 局限性

到目前为止，我们仅得出结论，总体相关性可能不为零。这是我们零假设方法的唯一结论，而且并没有真正令人感兴趣。我们真正想知道的是总体相关性。我们的0.25样本相关性似乎是一个合理的估计。我们将这样的单个数字称为点估计 (point estimate)。现在，一个新的样本可能会得出不同的相关性。一个有趣的问题是，如果我们抽取许多样本，我们的样本相关性会在样本中波动多少。下图精确地显示了这一点，假设我们的样本量为N = 100，并且我们对总体相关性的（点）估计为0.25。

零假设 - 备择假设下的抽样分布

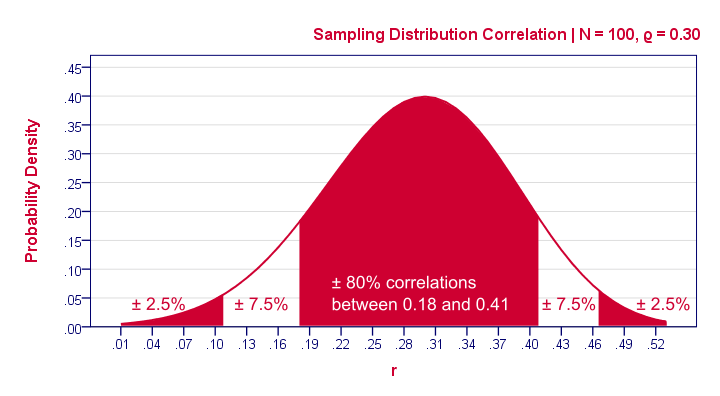
置信区间 (Confidence Intervals)

我们的样本结果表明，大约95％的许多样本应该得出0.06到0.43之间的相关性。此范围称为置信区间 (confidence interval)。虽然不完全正确，但最容易将其视为可能包含总体相关性的带宽。需要注意的一件事是，置信区间相当宽。它几乎包含零相关性，这正是我们之前拒绝的零假设。另一个需要注意的事情是，我们的抽样分布和置信区间略微不对称。对于大多数其他统计量（例如均值或beta系数 (beta coefficients)）而言，它们是对称的，但相关性不是。

参考文献

  1. Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
  2. Cohen, J (1988). Statistical Power Analysis for the Social Sciences (2nd. Edition). Hillsdale, New Jersey, Lawrence Erlbaum Associates.
  3. Field, A. (2013). Discovering Statistics with IBM SPSS Newbury Park, CA: Sage.
  4. Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
  5. Van den Brink, W.P. & Koele, P. (2002). Statistiek, deel 3 [统计学，第3部分]. Amsterdam: Boom.