SPSS 虚拟变量回归教程
作者:Ruben Geert van den Berg,发表于 回归 栏目下
在多元回归中使用分类预测变量需要进行虚拟编码(Dummy Coding)。那么,如何使用这些虚拟变量以及如何解释结果输出呢?本教程将引导你完成整个过程。
- 示例 I - 单个虚拟预测变量
- 示例 II - 多个虚拟预测变量
- 示例 III - 定量和虚拟预测变量
- 虚拟变量回归是否毫无用处?
示例数据
本教程中的所有示例都使用 staff-dummies.sav 数据文件,部分内容如下所示。
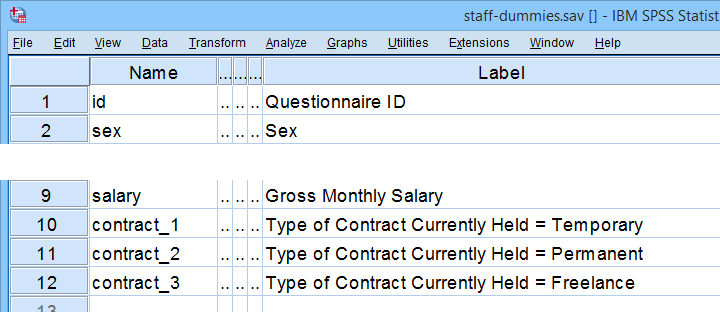
我们的数据文件已经包含代表合同类型的虚拟变量。在其他数据文件中创建此类虚拟变量的两种选择是:
- 我们的 虚拟变量工具
- 在 SPSS 中创建虚拟变量
分析 I - T 检验作为虚拟回归
我们首先检验月薪是否与性别有关。找到此答案的两种选择是:
- 独立样本 T 检验
- 以性别作为单个虚拟预测变量的简单线性回归。
这些分析得出的结果相同。比较这些结果是理解虚拟变量回归的第一步。我们首先从下面的 语法 运行 T 检验。
***独立样本 t 检验:薪水按性别分组。**
t-test groups sex(1 0)
/variables salary.结果
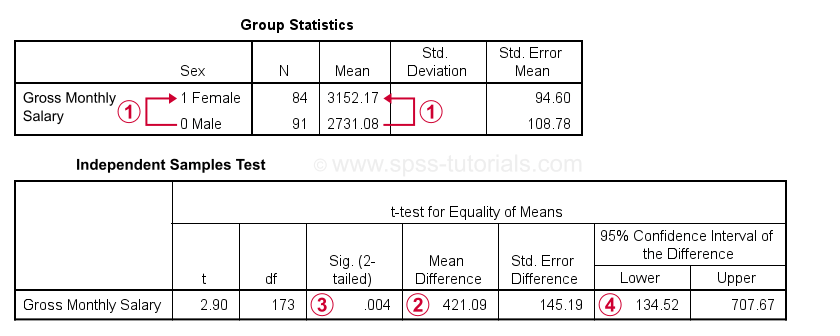
 女性的月薪总额比男性高 421.09 美元。另请注意,男性编码为 0,而女性编码为 1。
女性的月薪总额比男性高 421.09 美元。另请注意,男性编码为 0,而女性编码为 1。  此平均差异的 显著性水平 为 0.004:我们可能会拒绝男性和女性的总体平均工资相等的原假设。
此平均差异的 显著性水平 为 0.004:我们可能会拒绝男性和女性的总体平均工资相等的原假设。  95% 的置信区间表明总体平均差异的可能范围。它从 134.52 美元到 707.67 美元不等。
95% 的置信区间表明总体平均差异的可能范围。它从 134.52 美元到 707.67 美元不等。
现在,让我们将此分析重新运行为具有单个虚拟变量的回归。
示例 I - 单个虚拟预测变量
在 SPSS 中,我们首先导航到 A nalyze(分析)  R egression(回归)
R egression(回归)  L inear(线性),并填写如下所示的对话框。
L inear(线性),并填写如下所示的对话框。
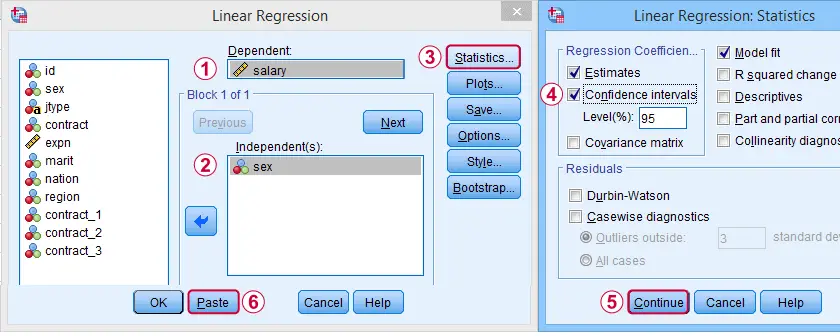
完成这些步骤会产生以下语法。让我们运行它。
***回归:薪水按单个虚拟变量(性别)分组。**
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT salary
/METHOD=ENTER sex.虚拟变量回归输出 I
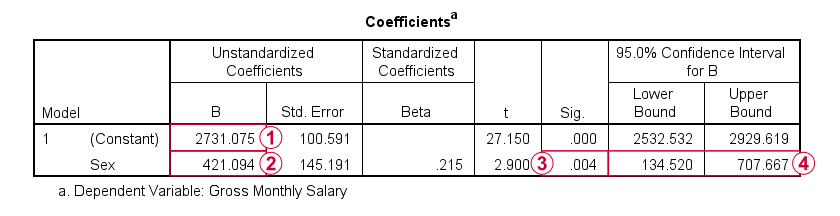
 请注意,常量(constant) 是男性受访者的平均薪水。
请注意,常量(constant) 是男性受访者的平均薪水。  性别的 b 系数(b-coefficient) 是男性和女性受访者之间的平均薪水差异。这等于与性别增加 1 个单位相关的平均薪水增加:从男性(编码为 0)到女性(编码为 1)。
性别的 b 系数(b-coefficient) 是男性和女性受访者之间的平均薪水差异。这等于与性别增加 1 个单位相关的平均薪水增加:从男性(编码为 0)到女性(编码为 1)。
这是有道理的,因为回归方程是:
\[Salary' = $2731 + $421 \cdot Sex\]
因此,对于所有 男性(males),我们预测月薪总额为:
\[Salary' = $2731 + $421 \cdot 0 = $2731\]
对于所有 女性(females),我们预测:
\[Salary' = $2731 + $421 \cdot 1 = $3152\]
这些预测的薪水只是男性和女性受访者的平均薪水。
最后,请注意, b 系数的显著性水平和
b 系数的显著性水平和  置信区间与其在 T 检验结果中平均差异的对应部分相同。
置信区间与其在 T 检验结果中平均差异的对应部分相同。
分析 II - ANOVA 作为虚拟回归
现在让我们看看薪水是否与合同类型(自由职业、临时或永久)有关。准确地说,我们将检验所有 3 种合同类型的总体平均薪水是否相等的原假设。检验此假设的两种选择是:
- ANOVA (方差分析)
- 虚拟变量回归。
正如我们将看到的,从我们的回归方法获得的 b 系数与 ANOVA 中的简单对比相同:指定 参考类别(reference category) 的平均值与每个其他类别的平均值进行比较。这些 ANOVA 结果可以从下面的语法中复制。
***ANOVA:薪水按合同类型分组。**
unianova salary by contract
/contrast (contract) = simple(1)
/print descriptive etasq.结果
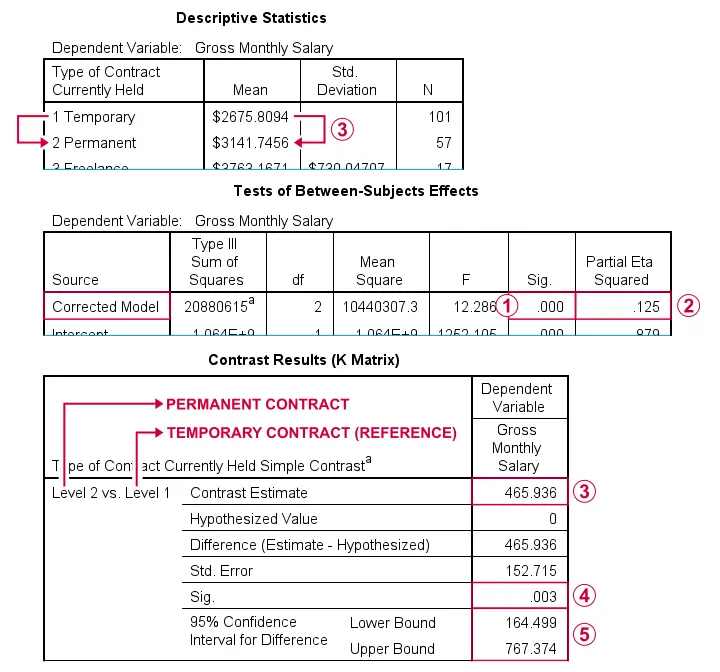
 由于 p < 0.05,我们拒绝所有总体平均值都相等的原假设。
由于 p < 0.05,我们拒绝所有总体平均值都相等的原假设。  效应量 (effect size),eta 平方为 0.125。这介于中等 (0.06) 和大 (0.14) 之间。
效应量 (effect size),eta 平方为 0.125。这介于中等 (0.06) 和大 (0.14) 之间。  永久合同员工与临时合同员工(参考类别)之间的平均差额为 465.94 美元。
永久合同员工与临时合同员工(参考类别)之间的平均差额为 465.94 美元。  p 值和
p 值和  置信区间表明此平均差额与零(此比较的原假设)存在“显著”差异。
置信区间表明此平均差额与零(此比较的原假设)存在“显著”差异。
类似地,比较自由职业员工与临时合同员工的平均薪水(此处未显示)。
示例 II - 多个虚拟预测变量
我们将导航到 A nalyze(分析)  R egression(回归)
R egression(回归) 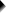 L inear(线性),并填写如下所示的对话框。
L inear(线性),并填写如下所示的对话框。
 我们需要选择一个参考类别,并且 不要 将其作为预测变量输入:对于表示 k 个类别,我们总是输入 (k - 1) 个虚拟变量。
我们需要选择一个参考类别,并且 不要 将其作为预测变量输入:对于表示 k 个类别,我们总是输入 (k - 1) 个虚拟变量。  完成这些步骤会生成以下语法。
完成这些步骤会生成以下语法。
***使用 2 个虚拟变量表示合同类型的回归。**
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT salary
/METHOD=ENTER contract_2 contract_3.虚拟变量回归输出 II
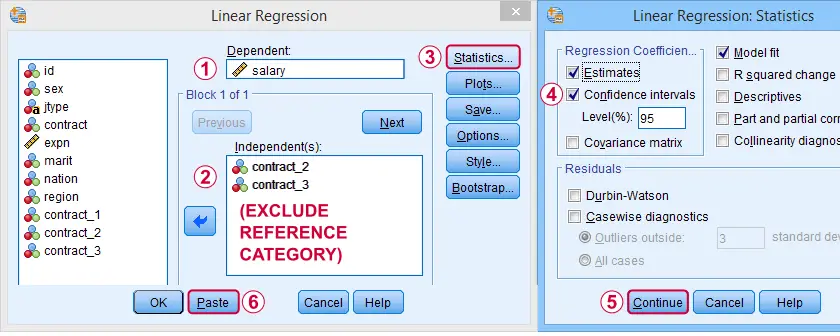
 请注意,r 平方(r-squared) 等于我们之前看到的 ANOVA eta 平方 (eta squared)。情况总是如此:这两个指标都表明因变量中由自变量解释的方差比例。
请注意,r 平方(r-squared) 等于我们之前看到的 ANOVA eta 平方 (eta squared)。情况总是如此:这两个指标都表明因变量中由自变量解释的方差比例。  整个模型(仅包含 2 个虚拟变量)的 R 平方在统计上是 显著的(significant)。事实上,整个回归 ANOVA 表与从实际 ANOVA 获得的表相同。
整个模型(仅包含 2 个虚拟变量)的 R 平方在统计上是 显著的(significant)。事实上,整个回归 ANOVA 表与从实际 ANOVA 获得的表相同。  常量(constant) 是我们的参考类别的平均薪水:签订临时合同的员工。这些受访者在我们模型中的两个虚拟变量上的得分均为零。对于他们来说,回归方程简化为:
常量(constant) 是我们的参考类别的平均薪水:签订临时合同的员工。这些受访者在我们模型中的两个虚拟变量上的得分均为零。对于他们来说,回归方程简化为:
\[Salary' = $2675.8 + $465.94 \cdot 0 + $1087.4 \cdot 0 = $2675.8\]
 b 系数(b-coefficients) 是每个虚拟类别和参考类别之间的平均差额:签订永久合同的员工的平均薪水比签订临时合同的员工高 465.94 美元。
b 系数(b-coefficients) 是每个虚拟类别和参考类别之间的平均差额:签订永久合同的员工的平均薪水比签订临时合同的员工高 465.94 美元。  永久合同员工和临时合同员工之间的平均薪水差在统计上与零“显著”不同,因为 p < 0.05。
永久合同员工和临时合同员工之间的平均薪水差在统计上与零“显著”不同,因为 p < 0.05。  所有 b 系数及其 p 值和置信区间与我们在早期 ANOVA 结果中看到的简单对比相同。
所有 b 系数及其 p 值和置信区间与我们在早期 ANOVA 结果中看到的简单对比相同。
关于这些结果的最后一点是,您应该输入代表同一分类变量的_所有_或_不_输入虚拟变量。如果您不这样做,则 b 系数不再对应于虚拟类别和参考类别之间的平均差额。下图试图澄清这个有些具有挑战性的点。

简而言之,虚拟变量代表某个类别与_所有_其他类别合并在一起。部分排除这些其他类别(参考类别除外)会隔离效应:这使得 b 系数等于虚拟类别与参考类别之间的平均差额。
分析 III - ANCOVA 作为虚拟回归
到目前为止,我们看到合同类型与平均薪水相关。但是,这仅仅是由于工作经验造成的吗?拥有更多工作年限的员工会获得更好的合同类型以及更高的薪水,仅仅是因为他们有更多经验?
排除这种可能的混淆的两种选择是:
- 以经验和 2 个合同类型虚拟变量作为预测变量的 多元回归分析。
- 以工作类型作为固定因子和经验作为协变量的 ANCOVA (协方差分析)。
我们首先将其分析为虚拟变量回归。然后,我们将通过 ANCOVA 方法复制结果。
示例 III - 定量和虚拟预测变量
同样,让我们导航到 A nalyze(分析)  R egression(回归)
R egression(回归) 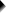 L inear(线性),并完成如下所示的步骤。
L inear(线性),并完成如下所示的步骤。
 对于此示例,我们将运行分层回归分析:我们首先只输入我们的控制变量 expn(工作经验)。
对于此示例,我们将运行分层回归分析:我们首先只输入我们的控制变量 expn(工作经验)。  然后,我们请求第二个“Block(块)”的预测变量。
然后,我们请求第二个“Block(块)”的预测变量。  最后,我们输入 2 个虚拟变量(排除 contract_1,我们的参考类别)作为我们的第二个块。
最后,我们输入 2 个虚拟变量(排除 contract_1,我们的参考类别)作为我们的第二个块。  这些步骤会产生以下语法。
这些步骤会产生以下语法。
***具有定量预测变量的分层回归,然后是 2 个虚拟变量。**
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA CHANGE
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT salary
/METHOD=ENTER expn
/METHOD=ENTER contract_2 contract_3.虚拟变量回归输出 III
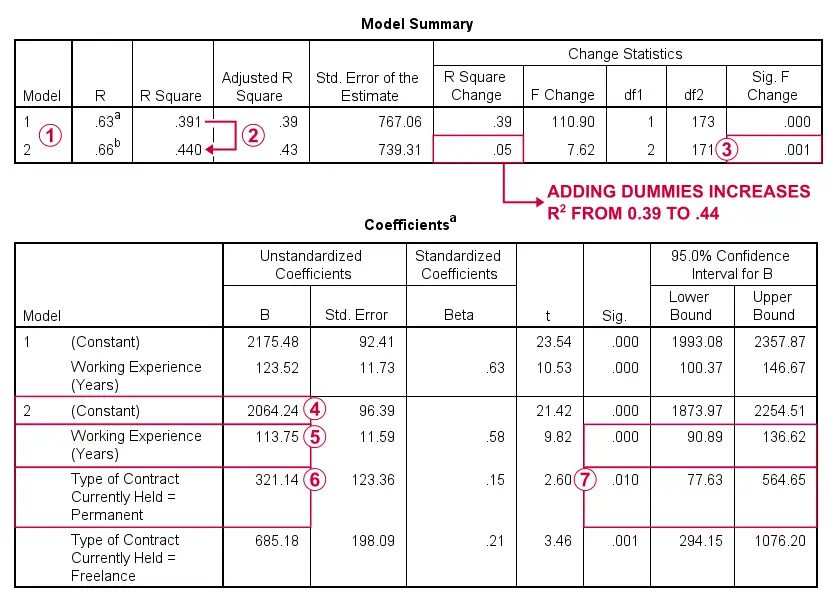
 SPSS 已经运行并比较了 2 个回归模型:模型 1(model 1) 包含工作经验作为(唯一的)定量预测变量。 模型 2(model 2) 将代表合同类型的 2 个虚拟变量添加到模型 1。
SPSS 已经运行并比较了 2 个回归模型:模型 1(model 1) 包含工作经验作为(唯一的)定量预测变量。 模型 2(model 2) 将代表合同类型的 2 个虚拟变量添加到模型 1。  将合同类型虚拟变量添加到工作经验会将 r 平方从 0.39 增加到 0.44。
将合同类型虚拟变量添加到工作经验会将 r 平方从 0.39 增加到 0.44。  这种增加在统计上是显著的:我们的虚拟变量有助于预测薪水,而不仅仅是工作经验。
这种增加在统计上是显著的:我们的虚拟变量有助于预测薪水,而不仅仅是工作经验。  模型 2 中的常量是 a) 签订临时合同(参考类别)和 b) 具有 0 年工作经验的员工的平均薪水。这些员工在模型 2 中的所有预测变量上的得分均为零。
模型 2 中的常量是 a) 签订临时合同(参考类别)和 b) 具有 0 年工作经验的员工的平均薪水。这些员工在模型 2 中的所有预测变量上的得分均为零。  如果我们控制合同类型,工作经验增加 1 个单位(年)与月薪平均增加 113.75 美元相关。
如果我们控制合同类型,工作经验增加 1 个单位(年)与月薪平均增加 113.75 美元相关。  如果我们控制工作经验,永久(虚拟)与临时(参考)合同员工之间的平均薪水差为 321.14 美元。
如果我们控制工作经验,永久(虚拟)与临时(参考)合同员工之间的平均薪水差为 321.14 美元。  由于 p < 0.05,此平均差异在统计上是显著的。
由于 p < 0.05,此平均差异在统计上是显著的。
现在,让我们从下面的语法中将完全相同的分析重新运行为 ANCOVA (协方差分析)。
***ANCOVA:薪水按合同分组,控制经验(年)。**
unianova salary by contract with expn
/contrast (contract) = simple(1)
/print descriptive etasq.结果
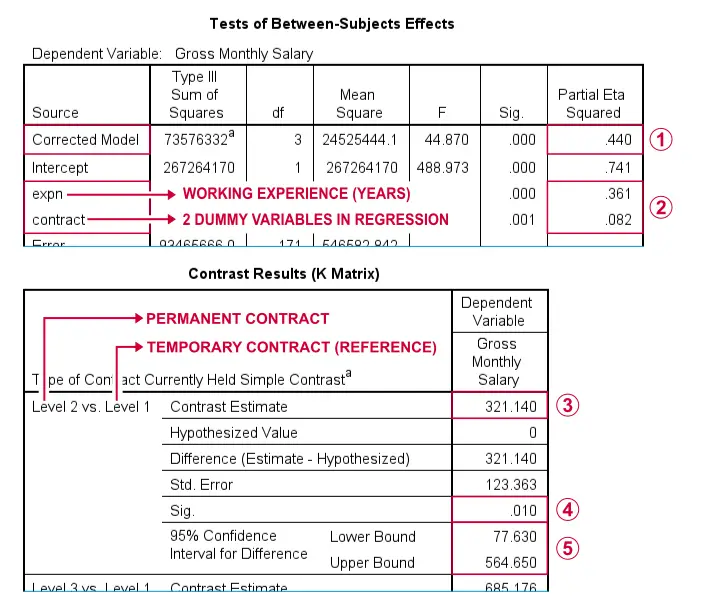
 “校正模型(corrected model)”的偏 eta 平方等于回归 r 平方。
“校正模型(corrected model)”的偏 eta 平方等于回归 r 平方。  输出还包含两个预测变量的单独效应量。请注意,0.361 和 0.082 加起来为 0.443,略大于整个模型的 0.440。这是因为这些效应部分重叠:经验与合同类型相关。
输出还包含两个预测变量的单独效应量。请注意,0.361 和 0.082 加起来为 0.443,略大于整个模型的 0.440。这是因为这些效应部分重叠:经验与合同类型相关。  如果我们校正工作经验,永久合同与临时合同员工之间的平均薪水差为 321.14 美元。此差异在之前的虚拟回归输出中被视为 b 系数。
如果我们校正工作经验,永久合同与临时合同员工之间的平均薪水差为 321.14 美元。此差异在之前的虚拟回归输出中被视为 b 系数。  毫不奇怪,p 值和
毫不奇怪,p 值和  置信区间 (confidence interval) 与其虚拟回归对应项也相同。
置信区间 (confidence interval) 与其虚拟回归对应项也相同。
虚拟变量回归是否毫无用处?
许多教科书都提出虚拟变量回归是使用定量和分类预测变量组合的唯一选择。但是,我们的最后一个例子表明,ANCOVA 可能是这种情况下的更好选择。为什么?好吧,
- ANCOVA 不需要向您的数据添加(技术上冗余的)虚拟变量。
- ANCOVA 为整个分类预测变量提出了一个单一的效应量(偏 eta 平方)。这比单独虚拟变量的效应量更有用,因为我们永远不会将它们单独添加到回归模型中。
- 通过 ANCOVA 相对容易地测试定量和分类预测变量之间的 调节效应 (moderation effects),但通过回归相当复杂。
最后的说明
首先,请注意本教程中的分析跳过了一些重要的步骤:
- 我们没有检查任何频率分布以查看我们的数据是否看起来合理;
- 我们没有看到我们的数据中是否有任何 缺失值 (missing values);
- 我们没有评估任何模型假设(正态性、线性等)。
我们鼓励您在处理真实世界的数据文件时彻底检查此类问题。
好的,这就是 SPSS 中虚拟回归的内容。有关所有 6 个分析的输出的便捷概述,请单击 此处。您是否发现本教程有(没有)帮助?您是否同意或不同意我们的观点?请在下面发表评论告诉我们。
感谢您的阅读!