变量转换正态化 – 6 个简单选项

作者：Ruben Geert van den Berg，发表于 SPSS Blog

转换概览

转换 (TRANSFORMATION)	适用情况 (USE IF)	局限性 (LIMITATIONS)	SPSS 示例 (SPSS EXAMPLES)
平方根/立方根 (Square/Cube Root)	变量呈现正偏态 (positive skewness)；残差呈现正异方差性 (positive heteroscedasticity)；变量包含频率计数 (frequency counts)。	平方根仅适用于正值。 (Square root only applies to positive values)	`compute newvar = sqrt(oldvar).` `compute newvar = oldvar**(1/3).`
对数 (Logarithmic)	分布呈正偏态 (positively skewed)。	自然对数 (Ln) 和常用对数 (log10) 仅适用于正值。	`compute newvar = ln(oldvar).` `compute newvar = lg10(oldvar).`
幂 (Power)	分布呈负偏态 (negatively skewed)。	无。(None)	`compute newvar = oldvar**3.`
倒数 (Inverse)	变量具有平峰分布 (platykurtic distribution)。	无法处理零。(Can’t handle zeroes)	`compute newvar = 1 / oldvar.`
双曲反正弦 (Hyperbolic Arcsine)	分布呈正偏态 (positively skewed)。	无。(None)	`compute newvar = ln(oldvar + sqrt(oldvar**2 + 1)).`
反正弦 (Arcsine)	变量包含比例 (proportions)。	无法处理绝对值 > 1 的值。(Can’t handle absolute values > 1)	`compute newvar = arsin(oldvar).`

正态化 – 是什么以及为什么？

“正态化 (Normalizing)” 意味着转换一个变量，使其更接近正态分布 (normally distributed)。许多统计程序都需要正态性假设 (normality assumption)：变量在某个总体中必须是正态分布。评估是否满足此假设的一些选项包括：

检查直方图 (histograms)；
检查偏度 (skewness)和峰度 (kurtosis)是否接近于零；
运行 Shapiro-Wilk 检验和/或 Kolmogorov-Smirnov 检验。

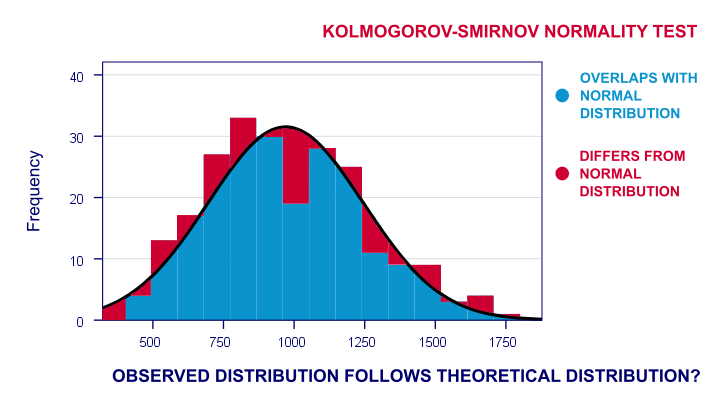
Kolmogorov Smirnov Normality Test What Is It Histogram

对于合理的样本量（例如，N ≥ 25），违反正态性假设通常没有问题：由于中心极限定理 (central limit theorem)，许多统计检验在这种情况下仍然产生准确的结果。那么，为什么要首先正态化任何变量呢？首先，一些统计量——特别是均值 (means)、标准差 (standard deviations) 和相关性 (correlations)——已被认为在技术上是正确的，但对于高度非正态变量仍然有些误导。

其次，我们还在多元回归分析 (multiple regression analysis)中遇到正态化转换，用于：

满足正态分布回归残差的假设 (assumption of normally distributed regression residuals)；
减少异方差性 (heteroscedasticity)；以及
减少因变量 (dependent variable) 和一个或多个预测变量 (predictors) 之间的曲线关系 (curvilinearity)。

正态化负值/零值

我们概览中的一些转换不适用于负值和/或零值。如果您的数据中存在此类值，您有两个主要选择：

仅转换非负和/或非零值；
向所有值添加一个常数，使其最小值 (minimum) 为 0、1 或其他某个正值。

第一种选择可能会导致许多缺失数据点，从而严重偏倚您的结果。或者，添加一个常数，将变量的最小值调整为 1，可以使用以下公式：

\[Pos_x = Var_x - Min_x + 1\]

这看起来像是一个不错的解决方案，但请记住，最小值为 1 是完全任意的：您可以选择 0.1、10、25 或任何其他正数。这是一个真正的问题，因为您选择的常数可能会影响变量在某些正态化转换之后的分布形状。这不可避免地会在您最终分析和报告的正态化变量中引入一些随意性。

测试数据

我们在 N = 1,000 的两个变量上尝试了概览中的所有转换：

var01 具有很强的负偏度 (negative skewness)，范围从 -1,000 到 +1,000；
var02 具有很强的正偏度 (positive skewness)，范围也从 -1,000 到 +1,000；

这些数据可从此 Googlesheet（只读）获得，部分内容如下所示。

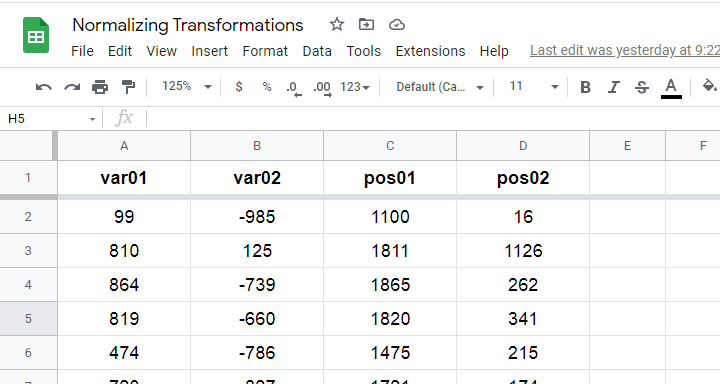
SPSS 用户可以下载与 normalizing-transformations.sav 完全相同的数据。

由于某些转换不适用于负值和/或零值，我们“positified”了两个变量：我们向它们添加了一个常数，使其最小值均为 1，从而得到 pos01 和 pos02。

尽管某些转换可以应用于原始变量，但“正态化”效果看起来非常令人失望。因此，我们决定将此讨论仅限于我们的 positified 变量。

平方根/立方根转换

如下所示，立方根转换在正态化我们的正偏态变量方面做得非常出色。

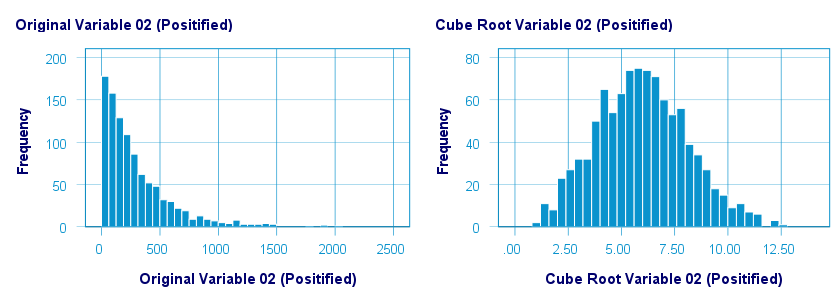
下图显示了原始值与转换后的值。

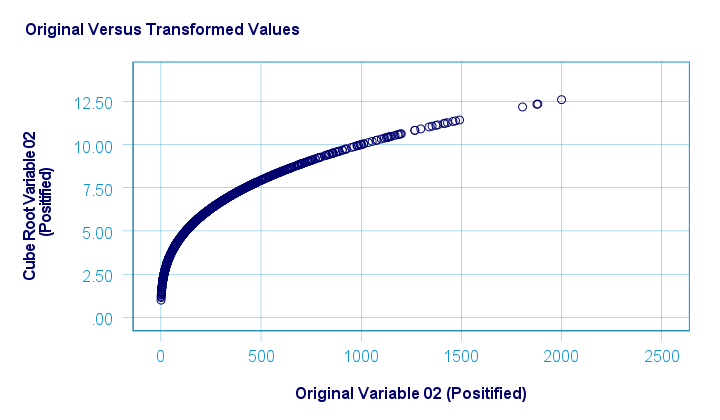
SPSS 拒绝计算负数的立方根。但是，下面的语法 (syntax) 包含解决此问题的简单方法。

***CUBE ROOT TRANSFORMATION.
**
compute curt01 = pos01**(1/3).
compute curt02 = pos02**(1/3).

***NOTE: IF VARIABLE MAY CONTAIN NEGATIVE VALUES, USE.
**
***if(pos01 >= 0) curt01 = pos01**(1/3).
** ***if(pos01 < 0) curt01 = -abs(pos01)**(1/3).
**
***HISTOGRAMS.
**
frequencies curt01 curt02
/format notable
/histogram.

***SCATTERPLOTS.
**
graph/scatter pos01 with curt01.
graph/scatter pos02 with curt02.

对数转换

以 10 为底的对数转换在正态化 var02 方面做得不错，但在 var01 方面则不然。一些结果如下所示。

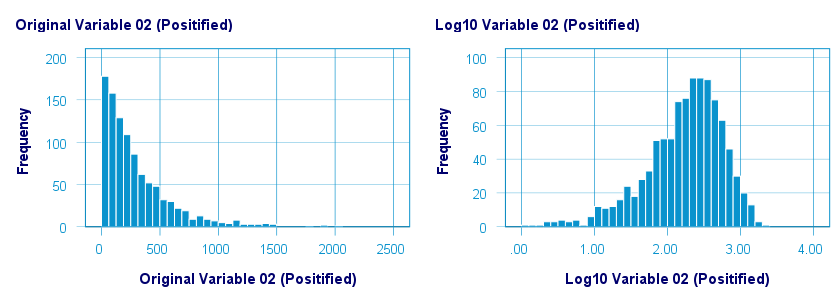
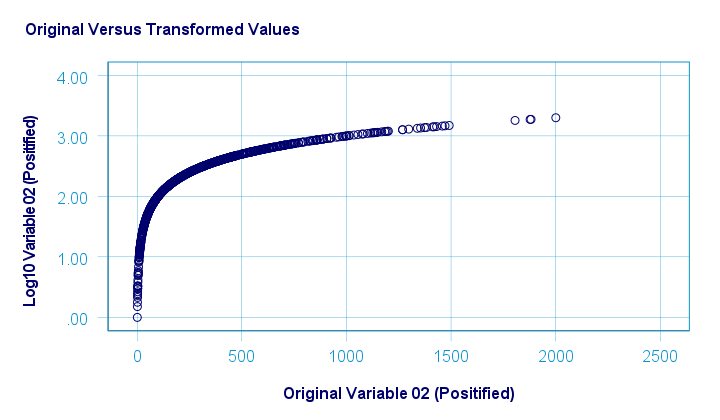
下图可视化了原始值与转换后的值。

SPSS 用户可以使用下面的语法 (syntax) 复制这些结果。

***LOGARITHMIC (BASE 10) TRANSFORMATION.
**
compute log01 = lg10(pos01).
compute log02 = lg10(pos02).

***HISTOGRAMS.
**
frequencies log01 log02
/format notable
/histogram.

***SCATTERPLOTS.
**
graph/scatter pos01 with log01.
graph/scatter pos02 with log02.

幂转换

三次幂（或立方）转换是对我们的左偏变量 (left skewed variable) 具有一些正态化效果的少数转换之一，如下所示。

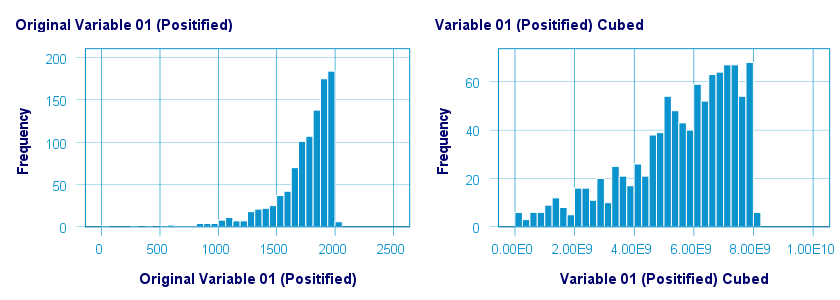
下图显示了此转换的原始值与转换后的值。

可以使用下面的语法 (syntax) 复制这些结果。

***THIRD POWER TRANSFORMATION.
**
compute cub01 = pos01**3.
compute cub02 = pos02**3.

***HISTOGRAMS.
**
frequencies cub01 cub02
/format notable
/histogram.

***SCATTERS.
**
graph/scatter pos01 with cub01.
graph/scatter pos02 with cub02.

倒数转换

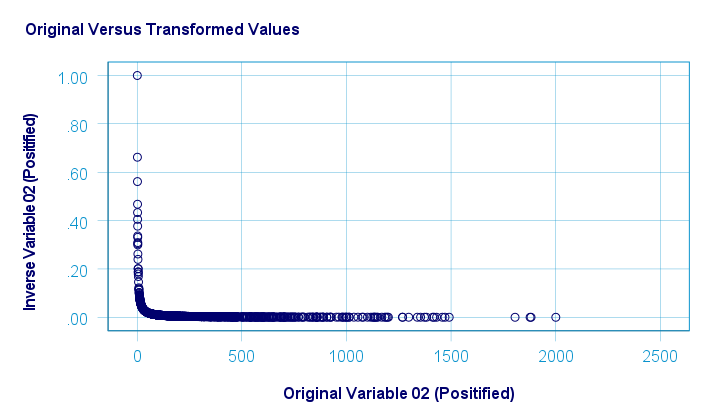
倒数转换在正态化两个变量方面都做得非常糟糕。下图可视化了转换前后 pos02 的分布。

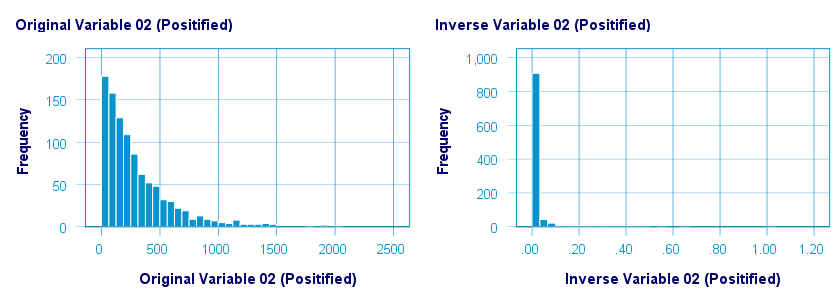
下图显示了原始值与转换后的值。此图表中出现极端模式的原因是将此变量的任意最小值设置为 1，如正态化负值中所讨论的那样。

SPSS 用户可以使用下面的语法 (syntax) 来复制这些结果。

***INVERSE TRANSFORMATION.
**
compute inv01 = 1 / pos01.
compute inv02 = 1 / pos02.

***NOTE: IF VARIABLE MAY CONTAIN ZEROES, USE.
**
***if(pos01 <> 0) inv01 = 1 / pos01.
**
***HISTOGRAMS.
**
frequencies inv01 inv02
/format notable
/histogram.

***SCATTERPLOTS.
**


graph/scatter pos01 with inv01.
graph/scatter pos02 with inv02.

双曲反正弦转换

如下所示，双曲反正弦转换对 var02 具有相当大的正态化效果，但对 var01 没有。

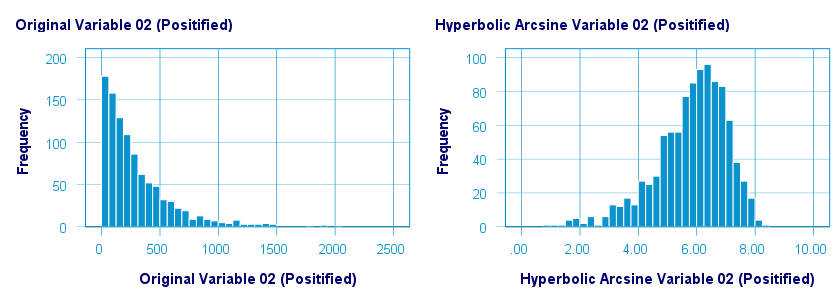
Hyperbolic Arcsine Transformation Histograms

下图绘制了原始值与转换后的值。

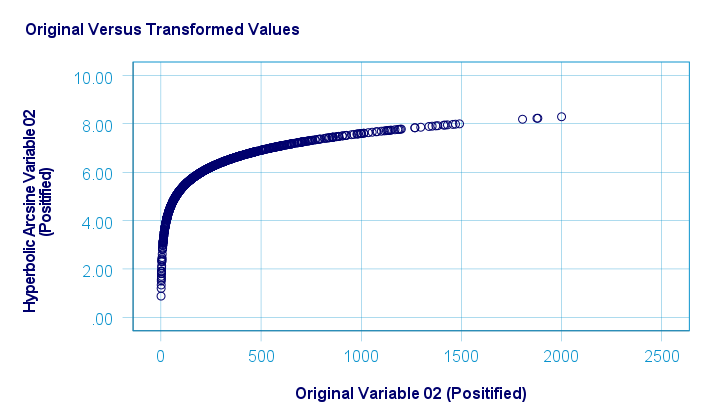
Hyperbolic Arcsine Transformation Function

在 Excel 和 Googlesheets 中，双曲反正弦根据 =ASINH(...) 计算。SPSS 中没有这样的函数，但一个简单的解决方法是使用

\[Asinh_x = ln(Var_x + \sqrt{Var_x^2 + 1})\]

下面的语法 (syntax) 正是这样做的。

***HYPERBOLIC ARCSINE TRANSFORMATION.
**
compute asinh01 = ln(pos01 + sqrt(pos01**2 + 1)).
compute asinh02 = ln(pos02 + sqrt(pos02**2 + 1)).

***HISTOGRAMS.
**
frequencies asinh01 asinh02
/format notable
/histogram.

***SCATTERS.
**
graph/scatter pos01 with asinh01.
graph/scatter pos02 with asinh02.

反正弦转换

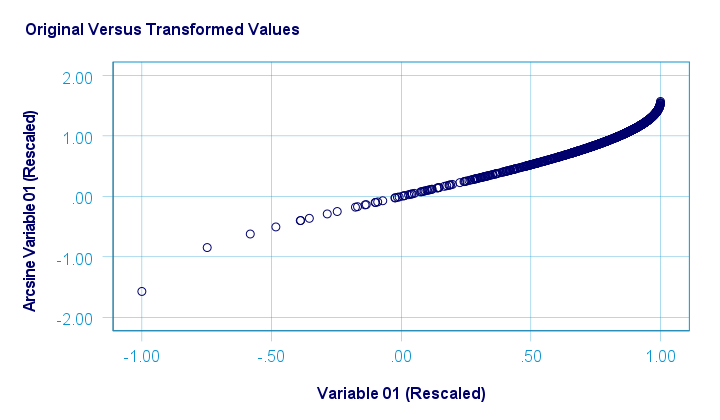
在应用反正弦转换之前，我们首先将两个变量重新缩放到 [-1, +1] 的范围。这样做之后，反正弦转换对两个变量都具有轻微的正态化效果。下图显示了 var01 的结果。

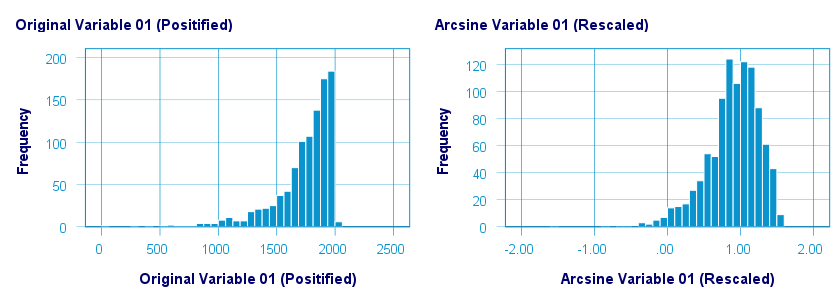
原始值与转换后的值在下图中可视化。

两个变量的重新缩放以及实际转换都是使用下面的 SPSS 语法 (syntax) 完成的。

***ADD MIN AND MAX AS NEW VARIABLES TO DATA.
**
aggregate outfile * mode addvariables
/min01 min02 = min(var01 var02)
/max01 max02 = max(var01 var02).

***RESCALE VARIABLES TO [-1, +1] .
**
compute trans01 = (var01 - min01)/(max01 - min01)*2 - 1.
compute trans02 = (var02 - min01)/(max01 - min01)*2 - 1.

***ARCSINE TRANSFORMATION.
**
compute asin01 = arsin(trans01).
compute asin02 = arsin(trans02).

***HISTOGRAMS.
**
frequencies asin01 asin02
/format notable
/histogram.

***SCATTERS.
**
graph/scatter trans01 with asin01.
graph/scatter trans02 with asin02.

转换后的描述性统计

下图总结了我们在所有转换前后原始变量的一些基本描述性统计 (descriptive statistics)。完整的表格可从此 Googlesheet（只读）获得。

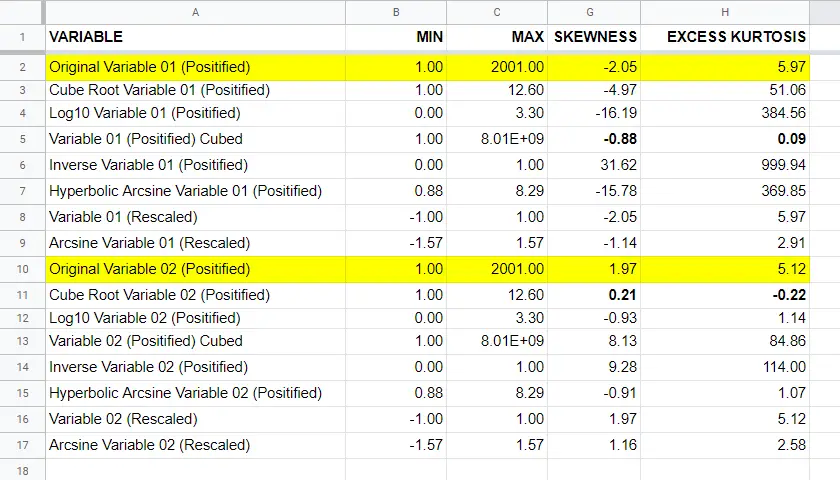
Descriptive Statistics After Normalizing Transformations

结论

如果我们仅根据每次转换后的偏度和峰度 (skewness and kurtosis) 来判断，那么对于我们的 2 个测试变量：

三次幂 (third power) 转换对我们的 左偏 (left skewed) 变量具有最强的正态化效果；
立方根 (cube root) 转换最适合我们的 右偏 (right skewed) 变量。

我应该补充一点，对于我们的左偏变量，没有一个转换做得真正好。

显然，这些结论仅基于 2 个测试变量。它们在多大程度上推广到更广泛的数据尚不清楚。但至少我们现在有了一些想法。