SPSS McNemar 检验

作者：Ruben Geert van den Berg，归类于非参数检验 & 统计 A-Z

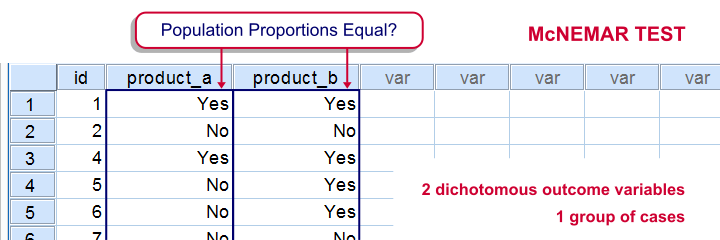
SPSS McNemar 检验是一种用于检验两个二分变量在某个总体中的比例是否相等的程序。这两个变量是在相同的案例中测量的。

SPSS McNemar 检验示例

一位营销人员想知道两种产品是否具有相同的吸引力。他请 20 名参与者试用这两种产品，并表明他们是否会考虑购买每种产品（“是”或“否”）。这产生了 product_appeal.sav 数据集。回答“是的，我会考虑购买”的受访者比例表明了每种产品的吸引力水平。 零假设 (null hypothesis) 是这两种百分比在总体中是相等的。

1. 快速数据检查

在进行统计程序之前，让我们先看看数据。对于在同一受访者身上测量的两个二分变量，一个基本上可以说明整个故事的图表是三维条形图。以下截图将引导您完成该过程。

我们首先导航到 G raph（图形） SPSS 菜单箭头 L egacy Dialogs（旧对话框） 3 -D Bar（三维条形图）单击 Define（定义）。

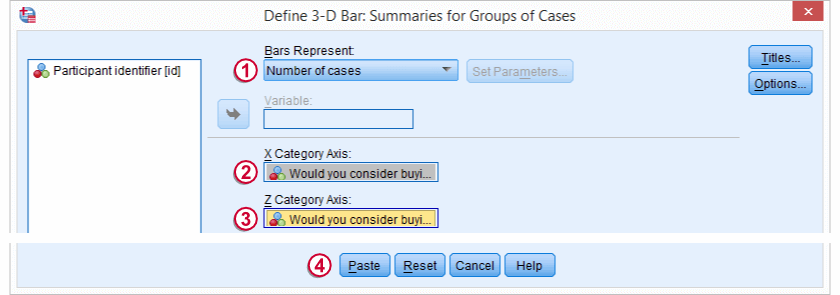
选择 Number of cases（个案数目）并将 product_a 和 product_b 移动到相应的框中。单击 P aste（粘贴）会生成以下语法。

***1. Set default directory.
**
cd 'd:\downloaded'. /*or wherever data file is located.

***2. Open data.
**
get file 'product_appeal.sav'.

***3.Quick data check.
**
XGRAPH CHART=([COUNT] [BAR]) BY product_a [c] BY product_b [c].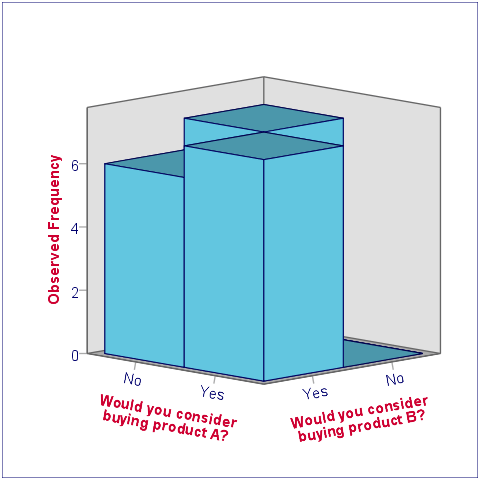

我们从该图表中学到的最重要的事情是，这两个变量确实是二分变量。可能存在一些“不知道/没有意见”的答案类别，但这两个变量只有“是”和“否”答案。没有系统缺失值 (system missing values) ，因为这些条形代表 (6 + 7 + 7 + 0 =) 20 个有效答案，这等于受访者的数量。其次，product_b 被 (6 + 7 =) 13 名受访者考虑，因此似乎比 product_a （被 7 名受访者考虑）更具吸引力。第三，所有考虑 product_a 的受访者也考虑 product_b ，但反之不然。这导致变量呈正相关，并要求仔细研究这两种产品的性质。

2. McNemar 检验的假设

McNemar 检验的结果仅依赖于一个假设：

独立且同分布的变量（或者，不太精确地说，“独立观察”）；

3. 运行 SPSS McNemar 检验

我们将导航到 A nalyze（分析） SPSS 菜单箭头 N onparametric Tests（非参数检验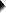） L egacy Dialogs（旧对话框） 2 Re l ated Samples（2 个相关样本）… 。

我们选择两个产品变量并将它们移动到 T est Pairs（检验配对）框中。在 O ptions（选项）下，我们将选择 D escriptives（描述性统计）。我们只在 T est Type（检验类型）下选择 M cNemar。单击 P aste（粘贴）会生成以下语法。

***Run McNemar Test.
**
NPAR TESTS
/MCNEMAR=product_a WITH product_b (PAIRED)
/STATISTICS DESCRIPTIVES.

4. SPSS McNemar 检验输出

第一个表（ Descriptive Statistics（描述性统计） ）确认没有缺失值。我们已经在图表中看到了这一点。如果有缺失值，这些描述性统计可能具有误导性。这是因为它们使用成对删除缺失值，而显著性检验（必须）使用列表删除缺失值。因此，描述性统计可能使用与实际检验不同的数据。可以通过在运行 McNemar 检验之前（手动） FILTERING 排除所有不完整的案例来规避此缺陷。请注意，SPSS 报告的是均值而不是比例。但是，如果您的答案类别编码为 0（表示“不存在”）和 1（表示“存在”），则均值与比例一致。我们建议您 RECODE 您的值，如果不是这种情况。比例（精确地）为 .35 和 .65。因此，差异为 -.3，我们预期为 0（比例相等）。

第二个表（ Test Statistics（检验统计量） ）显示 p 值为 .031。如果两个比例在总体中相等，那么找到我们在样本中观察到的差异的机会只有 3.1%。通常，如果 p < .05，我们拒绝零假设。因此，我们得出结论，两种产品的吸引力不相等。请注意，p 值是 双侧的 (two-sided) 。它包括找到小于（或等于） -.3 的差异的 .0155 的几率，以及找到大于（或等于） .3 的差异的另一个 .0155 的几率。

5. 报告 McNemar 检验结果

在任何情况下，我们都会报告两个比例以及它们所基于的样本大小，可能采用我们之前看到的描述性统计表的样式。对于报告显著性检验，我们可以写一些类似 “McNemar 检验表明两个比例不同，p = .031（双侧）。” 的内容。