SPSS 简单线性回归教程

作者：Ruben Geert van den Berg，发表于 回归 栏目下

  1. 创建带拟合线的散点图 (Create Scatterplot with Fit Line)
  2. SPSS 线性回归对话框 (SPSS Linear Regression Dialogs)
  3. 解读 SPSS 回归输出结果 (Interpreting SPSS Regression Output)
  4. 评估回归假设 (Evaluating the Regression Assumptions)
  5. APA 格式回归报告指南 (APA Guidelines for Reporting Regression)

研究问题与数据

X 公司让 10 名员工参加了智商 (IQ) 和工作表现测试。结果数据（部分如下所示）位于 simple-linear-regression.sav 文件中。

简单线性回归数据视图 (Simple Linear Regression Data View)

X 公司主要想弄清楚的是：智商 (IQ) 能否预测工作表现？如果可以，如何预测？我们将通过在 SPSS 中运行一个简单线性回归分析来回答这些问题。

创建带拟合线的散点图 (Create Scatterplot with Fit Line)

分析的一个很好的起点是散点图。它将告诉我们智商 (IQ) 和表现得分以及它们之间的关系（如果有的话）是否合理。我们将通过 “G raphs（图形）” SPSS 菜单箭头 (SPSS Menu Arrow) “L egacy Dialogs（旧对话框）” SPSS 菜单箭头 (SPSS Menu Arrow) “S catter/Dot（散点图/点图）” 创建我们的图表，然后按照下面的截图操作。

SPSS 简单线性回归散点图对话框 (SPSS Simple Linear Regression Scatterplot Dialog)

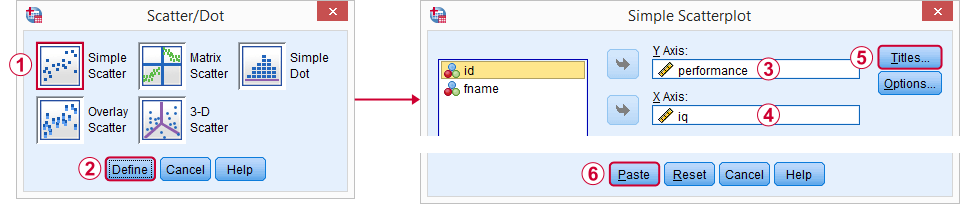
我个人喜欢添加：

  • 一个 标题，说明我的观众主要看的是什么；
  • 一个 副标题，说明显示的是哪些受访者或观察对象以及有多少。

完成对话框操作后，会生成以下 语法 (syntax)。让我们运行它。

SPSS 带标题和副标题的散点图语法 (SPSS Scatterplot with Titles Syntax)

***从 Graphs（图形） -> Legacy Dialogs（旧对话框） -> Scatter（散点图）创建带标题和副标题的散点图。**
GRAPH
/SCATTERPLOT(BIVAR)=iq WITH performance
/MISSING=LISTWISE
/TITLE='Scatterplot Performance with IQ'
/subtitle 'All Respondents | N = 10'.

结果

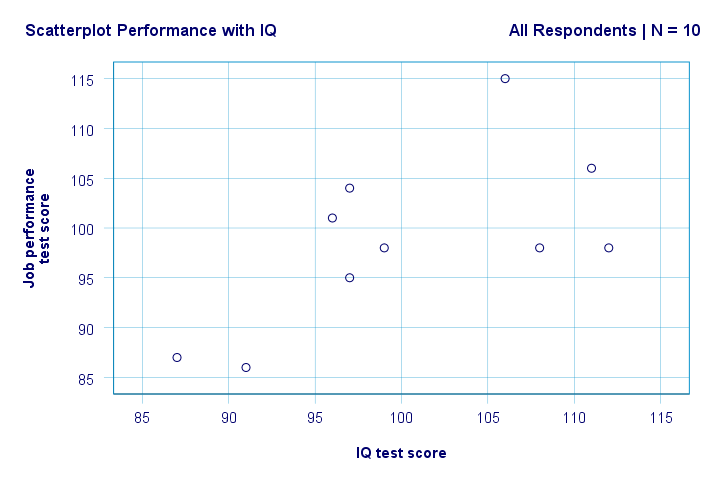
SPSS 简单线性回归散点图 (SPSS Simple Linear Regression Scatterplot)

好的。首先，我们在散点图中没有看到任何奇怪的东西。智商 (IQ) 和工作表现之间似乎存在中等程度的 相关性 (correlation)：平均而言，智商 (IQ) 得分较高的受访者似乎表现更好。这种关系看起来大致呈线性。现在让我们在散点图中添加 回归线 (regression line)。右 键单击该图，然后选择 “Edit c_o_ntent（编辑内容）” SPSS 菜单箭头 (SPSS Menu Arrow) “In Separate _W_indow（在单独窗口中）”，打开一个图表编辑器 (Chart Editor) 窗口。在这里，我们只需单击“Add Fit Line at Total（添加总计拟合线）”图标，如下所示。

SPSS 在散点图中添加拟合线 (SPSS Add Fit Line To Scatterplot)

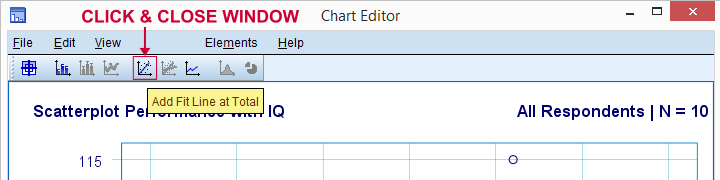
默认情况下，SPSS 现在将线性回归线添加到我们的散点图中。结果如下所示。

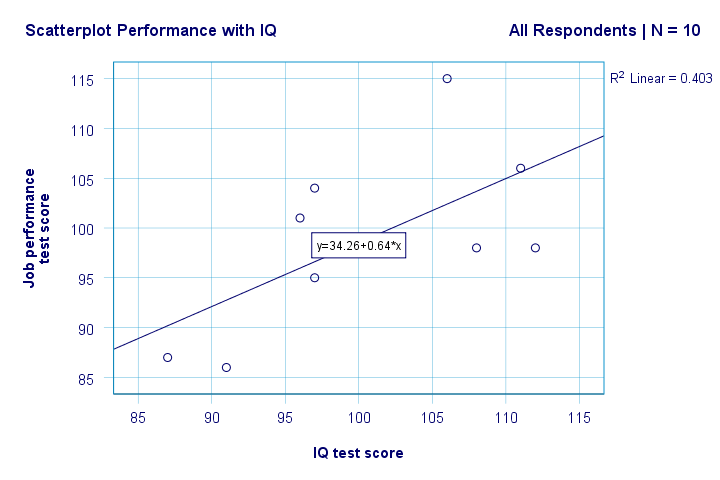
SPSS 带拟合线的散点图 (SPSS Scatterplot With Fit Line)

现在我们对研究问题有了一些初步的基本答案。R2 = 0.403 表明智商 (IQ) 解释了大约 40.3% 的工作表现得分方差。也就是说，智商 (IQ) 在这个样本中可以很好地预测工作表现。

但是，我们如何才能最好地根据智商 (IQ) 预测工作表现呢？在我们的散点图中，y 是工作表现（显示在 y 轴上），x 是智商 (IQ)（显示在 x 轴上）。所以公式是：performance = 34.26 + 0.64 * IQ。因此，对于智商 (IQ) 得分为 115 的求职者，我们预测他/她最有可能的未来工作表现得分为 34.26 + 0.64 * 115 = 107.86。

好的，这让我们对智商 (IQ) 和工作表现之间的关系有了一个基本的了解，并以可视化的方式呈现出来。但是，很多信息（统计显著性 (statistical significance) 和 置信区间 (confidence intervals)）仍然缺失。所以让我们去获取它。

SPSS 线性回归对话框 (SPSS Linear Regression Dialogs)

从 “A nalyze（分析）” SPSS 菜单箭头 (SPSS Menu Arrow) “R egression（回归）” SPSS 菜单箭头 (SPSS Menu Arrow) “L inear（线性）” 重新运行我们的最小回归分析会给我们提供更详细的输出。下面的截图显示了我们将如何进行操作。

SPSS 简单回归对话框 (SPSS Simple Regression Dialogs)

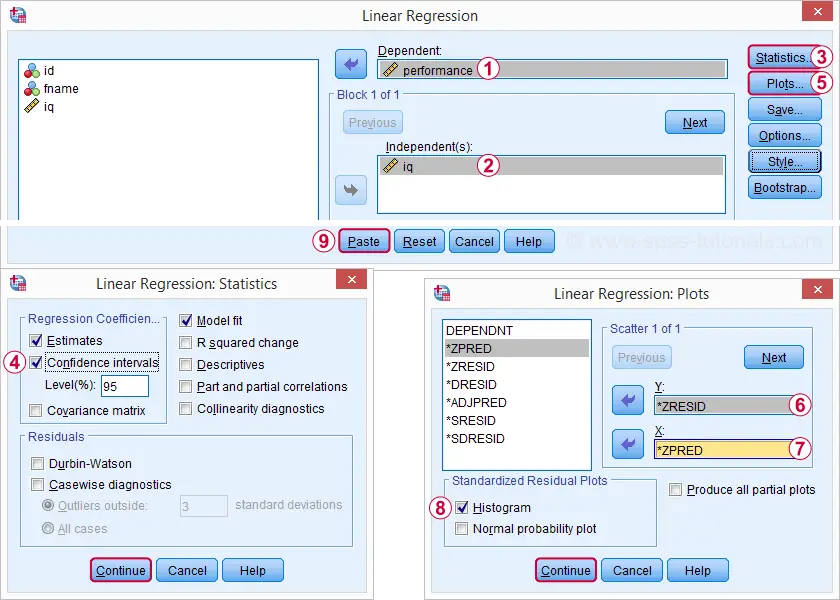
选择这些选项会生成以下语法。让我们运行它。

SPSS 简单线性回归语法 (SPSS Simple Linear Regression Syntax)

***带有残差图和置信区间的简单回归。**
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT performance
/METHOD=ENTER iq
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID).

SPSS 回归输出 I - 系数 (SPSS Regression Output I - Coefficients)

不幸的是，SPSS 给我们的回归输出比我们需要的多得多。我们可以安全地忽略其中的大部分。但是，一个非常重要的表格是下面的 系数表 (coefficients table)。

SPSS 简单线性回归系数表 (SPSS Simple Linear Regression Coefficients Table)

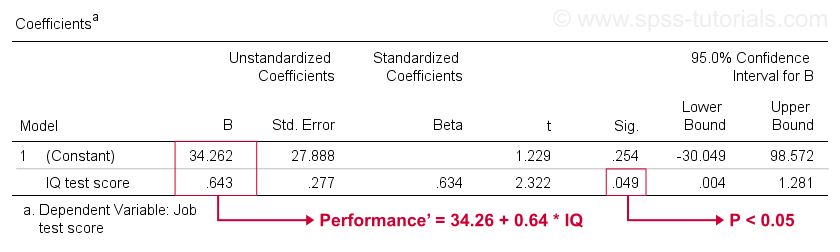
该表显示了我们在散点图中已经看到的 B 系数。正如所指出的，这些系数暗示了线性回归方程，该方程最好地估计了我们的样本中智商 (IQ) 对工作表现的影响。

其次，请记住，如果 p < 0.05，我们通常会拒绝零假设。智商 (IQ) 的 B 系数的 “Sig” 或 p = 0.049。它在统计上与零显着不同。

但是，它的 95% 置信区间（大致来说，是其总体值的可能范围）是 [0.004, 1.281]。所以 B 可能不是零，但它可能非常接近于零。置信区间很大——我们对 B 的估计根本不精确——这是由于分析所基于的最小样本量造成的。

SPSS 回归输出 II - 模型摘要 (SPSS Regression Output II - Model Summary)

除了系数表 (coefficients table) 之外，我们还需要 模型摘要表 (Model Summary table) 来报告我们的结果。

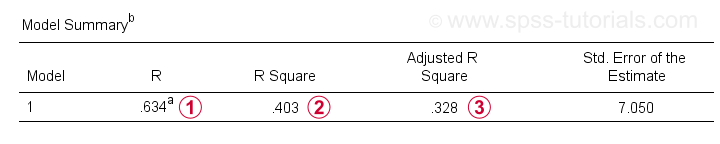
SPSS 简单回归 - 模型摘要表 (SPSS Simple Regression - Model Summary Table)

R 是回归预测值和实际值之间的相关性。对于简单回归，R 等于预测变量和因变量之间的相关性。

R Square（R 平方）——平方相关性——表示因变量中由我们样本数据中的预测变量解释的方差比例。

调整后的 R 平方 (Adjusted R-square) 估计了当我们把基于（样本的）回归方程应用于整个总体时，R 平方的值。

调整后的 R 平方比简单的 R 平方更能真实地估计预测的准确性。在我们的例子中，它们之间巨大的差异（通常被称为收缩）是由于我们非常小的样本量 N = 10 造成的。

无论如何，这对 X 公司来说是个坏消息：智商 (IQ) 实际上并没有那么好地预测工作表现。

评估回归假设 (Evaluating the Regression Assumptions)

回归的主要假设是：

  1. 独立观察 (Independent observations)；

  2. 正态性 (Normality)：误差在总体中必须服从正态分布；

  3. 线性 (Linearity)：每个预测变量和因变量之间的关系是线性的；

  4. 同方差性 (Homoscedasticity)：误差必须在所有预测值水平上具有恒定的方差。

  5. 如果 SPSS 中的每个个案（数据视图中的单元格行）代表一个个体，我们通常假设这些是 “独立观察 (Independent observations)”。接下来，最好通过检查我们输出中的回归图来评估假设 2-4。

  6. 如果 正态性 (normality) 成立，那么我们的回归残差应该（大致）服从正态分布 (normally distributed)。下面的直方图没有显示出明显的偏离正态性。

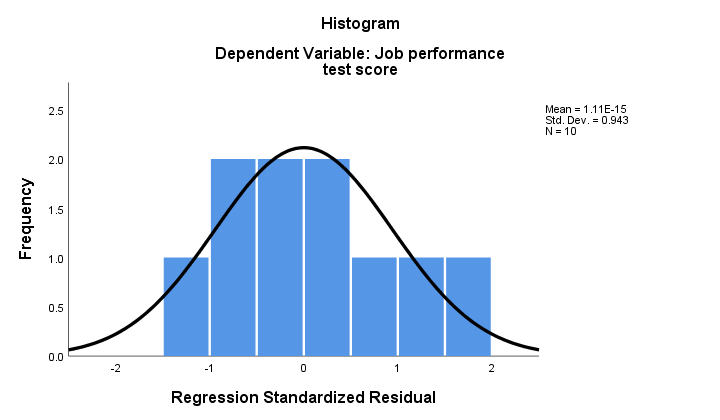
SPSS 简单回归残差服从正态分布 (SPSS Simple Regression Residuals Normally Distributed)

回归过程可以将这些残差作为新变量添加到您的数据中。通过这样做，您 可以 对它们运行 Kolmogorov-Smirnov 检验 (Kolmogorov-Smirnov test)，以检验其正态性。但是，对于手头的小样本，此测试几乎没有任何 统计功效 (statistical power)。所以让我们跳过它。

  1. 线性 (linearity) 和 4. 同方差性 (homoscedasticity) 假设最好通过残差图来评估。这是一个散点图，其中 x 轴是预测值，y 轴是残差，如下所示。两个变量都已标准化，但这不会影响点模式的形状。

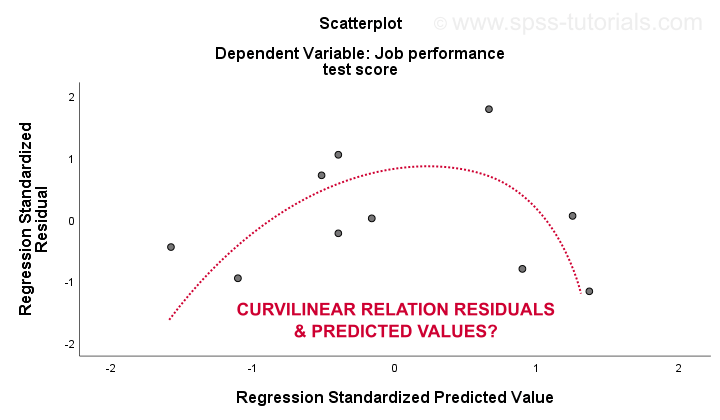
回归残差图曲线 (Regression Residual Plot Curvilinearity)

老实说，残差图显示出强烈的曲线关系。我手动绘制了我认为最适合整体模式的曲线。假设曲线关系可能也会解决异方差性，但现在事情变得太技术性了。基本点很简单，就是某些假设不成立。对于这些问题，最常见的解决方案（从最差到最好）是：

  • 完全 忽略 (ignoring) 这些假设；
  • 谎称 (lying) 回归图没有表明任何违反模型假设的情况；
  • 对因变量进行非线性 转换 (transformation)，例如 对数转换 (logarithmic)；
  • 拟合 曲线 (curvilinear) 模型 - 我们稍后会尝试一下。

APA 格式回归报告指南 (APA Guidelines for Reporting Regression)

下图是（从字面上看）用于以 APA 格式报告回归的教科书式图示。

Apa 格式线性回归报告 (Apa Reporting Linear Regression)

从 SPSS 输出创建这个精确的表格是非常痛苦的。在 Excel 中编辑它比在 WORD 中更容易，因此这至少可以为您节省一些麻烦。

或者，尝试复制粘贴（未经编辑的）SPSS 输出并假装不知道确切的 APA 格式。

非线性回归实验 (Non Linear Regression Experiment)

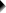我们的样本量太小，无法真正拟合线性模型之外的任何模型。但我们还是这样做了——只是出于好奇。SPSS 中最简单的选项是 “A nalyze（分析）” SPSS 菜单箭头 (SPSS Menu Arrow) “R egression（回归）” SPSS 菜单箭头 (SPSS Menu Arrow) “C urve Estimation（曲线估计）”。我们不会讨论对话框，但我们粘贴了下面的语法。

SPSS 非线性回归语法 (SPSS Non Linear Regression Syntax)

***从 Analyze（分析）- Regression（回归）- Curve Estimation（曲线估计）进行非线性回归。**
TSET NEWVAR=NONE.
CURVEFIT
/VARIABLES=performance WITH iq
/CONSTANT
/MODEL= quadratic linear
/PLOT FIT.

结果

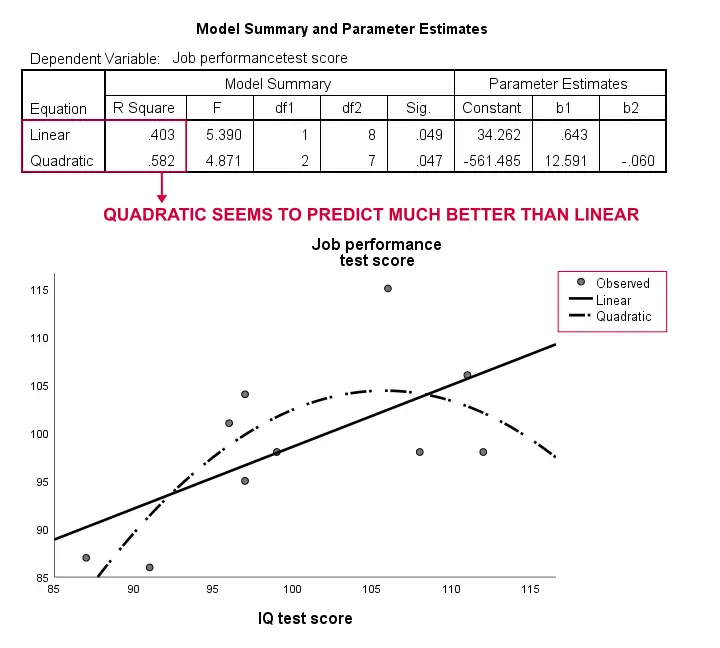
SPSS 非线性回归结果 (SPSS Non Linear Regression Results)

同样，我们的样本太小，无法得出任何严肃的结论。但是，结果确实表明曲线模型比线性模型更适合我们的数据。我们不会进一步探讨这一点，但我们确实想提一下；我们认为社会科学家通常会忽视曲线模型。

感谢阅读！