SPSS 逐步回归教程 II
作者:Ruben Geert van den Berg,发表于 回归
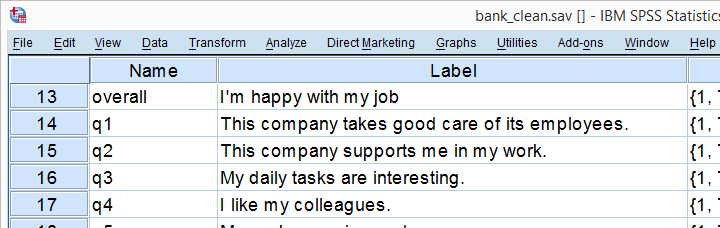
一家大型银行希望深入了解员工的工作满意度。他们进行了一项调查,结果保存在 bank_clean.sav 文件中。调查包括一些关于工作满意度的陈述,如下所示。
研究问题
今天的主要研究问题是:哪些因素对整体工作满意度贡献最大?**** 以 “I’m happy with my job (我对我的工作很满意)” (变量名:overall) 作为衡量标准。回答这个问题的常用方法是使用多元线性回归分析 (multiple linear regression analysis) 从这些因素 预测 工作满意度。 2 , 6 本教程将解释和演示涉及的每个步骤,我们鼓励您通过下载数据文件自己运行这些步骤。
数据检查 1 - 编码 (Coding)
在对数据运行任何分析之前,最好先了解数据中的内容,这是 SPSS 的最佳实践之一。我们的分析将使用 overall 到 q9 这些变量,它们的变量标签告诉我们它们的含义。现在,如果我们在 数据视图 (data view) 中查看这些变量,我们看到它们包含值 1 到 11。
那么这些值是什么意思?重要的是,对于所有变量,它们的含义是否相同?一个很好的方法是运行以下语法。
***检查编码:较高的值表示积极还是消极情绪?
**
display dictionary
/variables overall to q9.结果
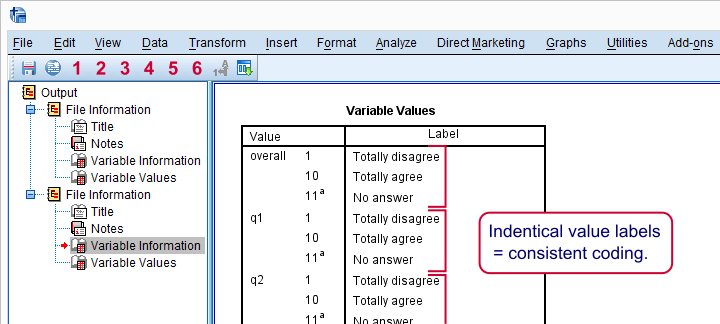
如果我们快速检查这些表,我们会看到两个重要的内容:
- 对于所有陈述,较高的值表示更强的赞同;
- 所有陈述都是积极的(“喜欢”而不是“不喜欢”):更多的赞同表示更积极的情绪。
将这些发现放在一起,我们期望所有这些变量之间存在正 (而不是负) 相关性 (correlations)。我们稍后会看到我们的数据证实了这一点。
数据检查 2 - 分布 (Distributions)
我们之前的表格 表明 所有变量都包含值 1 到 11,并且 11 (“没有答案”) 已经被设置为 用户缺失值 (user missing value)。现在让我们通过运行一些直方图来查看这些变量的分布是否有意义。
***检查分布。
**
frequencies overall to q9
/format notable
/histogram.数据检查 3 - 缺失值 (Missing Values)
首先,所有变量的分布都显示值 1 到 10,并且它们看起来是合理的。但是,我们总共有 464 个案例,但我们的直方图显示略低的样本量。这是由于缺失值。为了快速了解缺失值的程度,我们将在它们上面运行一个快速 DESCRIPTIVES 表。
***1. 仅在输出中显示变量标签。
**
set tvars labels.
***2. 检查缺失值和列表删除有效样本量(listwise valid n)。
**
descriptives overall to q9.结果
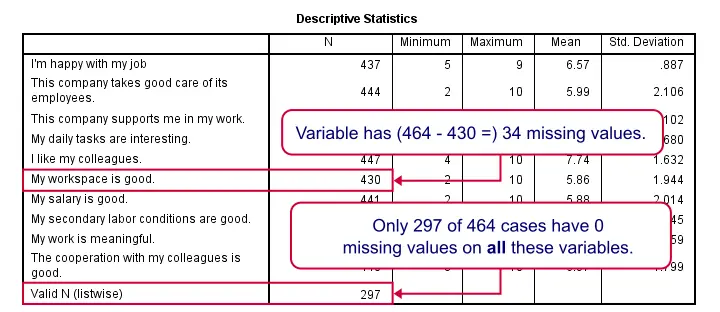
目前,我们主要关注 N,即每个变量的有效值的数量。我们看到两个重要的内容:
- 最低的 N 为 430(“My workspace is good (我的工作空间很好)”),在 464 个案例中;大约 7% 的值缺失。
- 只有 297 个案例在此表中的所有变量上都没有缺失值。
相关性 (Correlations)
我们现在将检查变量之间的相关性,如下所示。
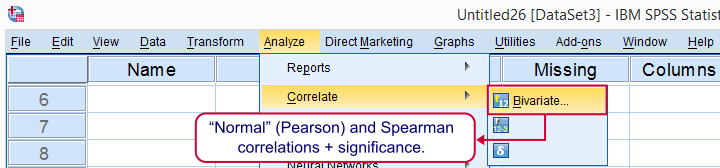
在下一个对话框中,我们选择所有相关变量,并保持其他所有内容不变。然后我们单击 P aste,生成以下语法。
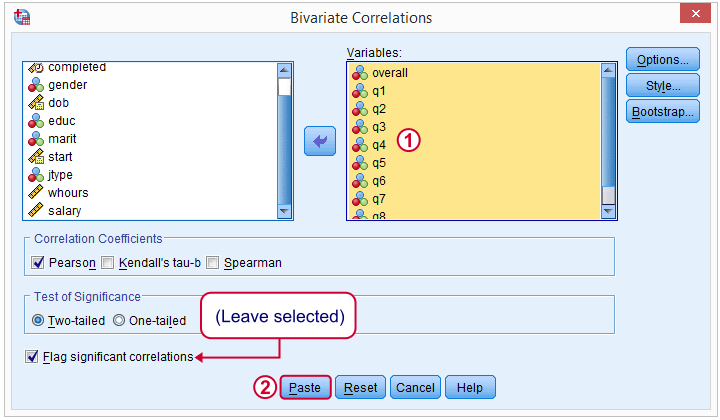
***检查相关性。
**
CORRELATIONS
/VARIABLES=overall q1 q2 q3 q4 q5 q6 q7 q8 q9
/PRINT=TWOTAIL NOSIG
/MISSING=PAIRWISE.重要的是,请注意最后一行 - /MISSING=PAIRWISE. - 在这里。
结果

请注意,所有相关性都是正的 - 就像我们预期的那样。大多数相关性 - 即使是很小的相关性 - 在统计上都是显著的,p 值 (p-values) 接近 0.000。这意味着如果总体相关性为零,则找到此样本相关性的概率为零。
其次,每个相关性都是根据所有在涉及的 2 个变量上具有有效值的案例计算的,这就是为什么每个相关性具有不同的 N。这被称为成对排除缺失值 (pairwise exclusion of missing values),CORRELATIONS 的默认设置。
另一种方法是列表删除缺失值 (listwise exclusion of missing values),它只会使用我们的 297 个案例,这些案例在涉及的 任何 变量上都没有缺失值。像这样,成对排除比列表删除使用更多的数据****值;使用列表删除,我们将“丢失”几乎 36% 或我们收集的数据。
多元线性回归 - 假设 (Assumptions)
简单地“回归”通常指的是(单变量)多元线性回归分析,它需要一些假设:1 , 4
- 预测误差在案例之间是独立的 (independent);
- 预测误差遵循正态分布 (normal distribution);
- 预测误差具有恒定的方差(同方差性 (homoscedasticity));
- 变量之间的所有关系都是线性的 (linear) 且可加的 (additive)。
我们通常在运行分析之前检查我们的假设。但是,回归假设主要通过检查运行分析时创建的一些图表来评估。 3 所以我们首先运行我们的回归,然后寻找违反上述假设的任何情况。
回归 (Regression)
现在我们确信我们的数据完全有意义,我们准备进行实际的回归分析。我们将通过以下屏幕截图生成语法。
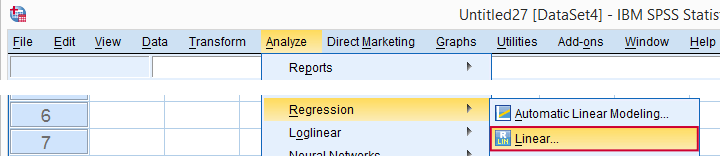
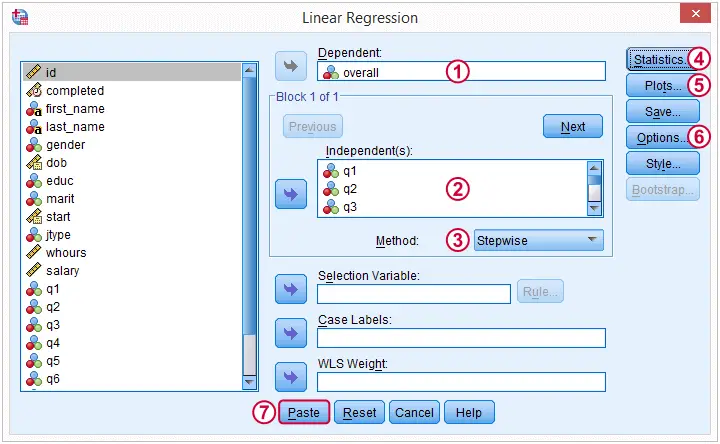
(我们将在讨论我们的输出时解释为什么我们选择 Stepwise 逐步回归。)
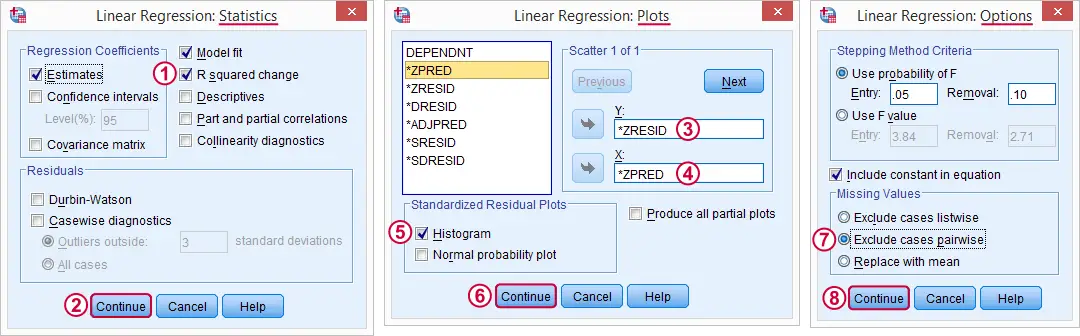
 -
-  在这里,我们选择一些图表用于评估回归假设。
在这里,我们选择一些图表用于评估回归假设。  默认情况下,SPSS 仅使用我们的 297 个完整案例进行回归。通过选择此选项,我们的回归将使用我们之前看到的相关矩阵,从而使用更多的数据。
默认情况下,SPSS 仅使用我们的 297 个完整案例进行回归。通过选择此选项,我们的回归将使用我们之前看到的相关矩阵,从而使用更多的数据。
“逐步回归 (Stepwise)” - 那是什么意思?
当我们选择逐步回归方法时,SPSS 将仅包含“显著”预测变量在我们的回归模型中:虽然我们选择了 9 个预测变量,但那些对预测工作满意度没有唯一贡献的预测变量 不会 进入我们的回归方程。这样做时,它会迭代执行以下步骤:
- 找到对预测结果变量贡献最大的预测变量,如果其 p 值低于某个阈值(通常为 0.05),则将其添加到回归模型中。
- 检查模型中所有预测变量的 p 值。如果预测变量的 p 值高于某个阈值(通常为 0.10),则从模型中删除预测变量;
- 重复此过程,直到 1) 所有“显著”预测变量都在模型中,并且 2) 模型中没有“非显著”预测变量。
回归结果 - 系数表 (Coefficients Table)
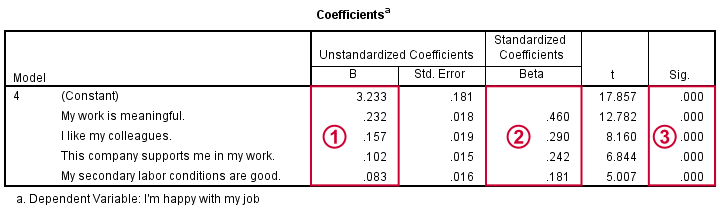
我们的系数表告诉我们 SPSS 执行了 4 个步骤,在每个步骤中添加一个预测变量。我们通常只报告最终模型。  我们的未标准化系数 (unstandardized coefficients) 和常数项 (constant) 允许我们预测工作满意度。确切地说,Y’ = 3.233 + 0.232 * x1 + 0.157 * x2 + 0.102 * x3 + 0.083 * x4,其中 Y’ 是预测的工作满意度,x1 是意义感 (meaningfulness),依此类推。这意味着在意义感 (meaningfulness) 上得分高 1 分的受访者,平均而言,其工作满意度得分高 0.23 分。
我们的未标准化系数 (unstandardized coefficients) 和常数项 (constant) 允许我们预测工作满意度。确切地说,Y’ = 3.233 + 0.232 * x1 + 0.157 * x2 + 0.102 * x3 + 0.083 * x4,其中 Y’ 是预测的工作满意度,x1 是意义感 (meaningfulness),依此类推。这意味着在意义感 (meaningfulness) 上得分高 1 分的受访者,平均而言,其工作满意度得分高 0.23 分。
重要的是,所有预测变量都对工作满意度做出 积极(而不是消极)的贡献。这是有道理的,因为它们都是积极的工作方面。  如果我们的预测变量具有不同的尺度 - 在这里并非如此 - 我们可以通过标准化它们来比较它们的相对强度 - beta 系数 (beta coefficients)。像这样,我们看到意义感 (meaningfulness) (.460) 的贡献大约是同事关系 (colleagues) (.290) 或支持 (support) (.242) 的两倍。
如果我们的预测变量具有不同的尺度 - 在这里并非如此 - 我们可以通过标准化它们来比较它们的相对强度 - beta 系数 (beta coefficients)。像这样,我们看到意义感 (meaningfulness) (.460) 的贡献大约是同事关系 (colleagues) (.290) 或支持 (support) (.242) 的两倍。  考虑到我们的大样本量和我们使用的逐步回归方法,所有预测变量在统计上都非常显著 (highly statistically significant)(p = 0.000),这并不奇怪。
考虑到我们的大样本量和我们使用的逐步回归方法,所有预测变量在统计上都非常显著 (highly statistically significant)(p = 0.000),这并不奇怪。
回归结果 - 模型摘要 (Model Summary)
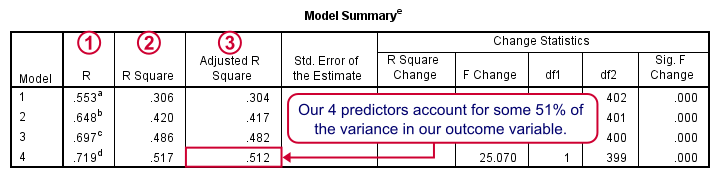
在我们的逐步回归过程中添加每个预测变量都会导致更好的预测准确性。  R 只是工作满意度的实际值和预测值之间的 Pearson 相关性 (Pearson correlation);
R 只是工作满意度的实际值和预测值之间的 Pearson 相关性 (Pearson correlation);  R 平方 (R square) - 相关性的平方 - 是预测值解释的工作满意度方差的比例;
R 平方 (R square) - 相关性的平方 - 是预测值解释的工作满意度方差的比例;  我们通常看到我们的回归方程在其所基于的样本中表现更好,而不是在我们的总体中。调整后的 R 平方 (Adjusted R square) 试图估计我们在总体中的预测准确性,并且略低于 R 平方。
我们通常看到我们的回归方程在其所基于的样本中表现更好,而不是在我们的总体中。调整后的 R 平方 (Adjusted R square) 试图估计我们在总体中的预测准确性,并且略低于 R 平方。
我们可能会满足于 - 并报告 - 我们的最终模型;系数看起来不错,它可以最好地预测工作绩效。
回归结果 - 残差直方图 (Residual Histogram)
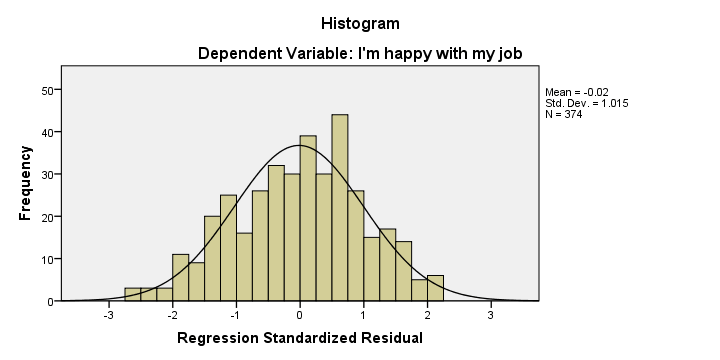
请记住,我们的 回归假设 之一是残差(预测误差)呈正态分布。我们的直方图表明这或多或少成立,尽管它有点向左倾斜。
回归结果 - 残差图 (Residual Plot)
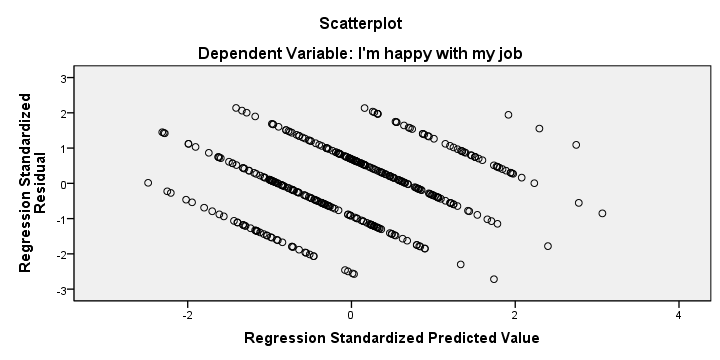
我们还创建了一个 散点图 (scatterplot),x 轴上是预测值,y 轴上是残差。该图表未显示违反独立性 (independence)、同方差性 (homoscedasticity) 和线性 (linearity) 假设的情况,但不是很清楚。
我们主要看到一个引人注目的下降直线模式。这是因为我们的因变量只包含值 1 到 10。因此,每个预测值及其残差始终加起来等于 1、2 等等。
标准化两个变量可能会改变我们散点图的尺度,但不会改变其形状。
逐步回归 - 报告 (Reporting)
关于如何报告逐步回归分析,没有完全一致的意见。 5 , 7 作为基本指南,包括
- 包含描述性统计 (descriptive statistics) 的表;
- 因变量和所有(候选)预测变量的相关矩阵 (correlation matrix);
- 包含 R 平方 (R square) 的模型摘要表和每个模型的 R 平方变化;
- 至少包含 B 和 β 系数及其 p 值的系数表 (coefficients table)。
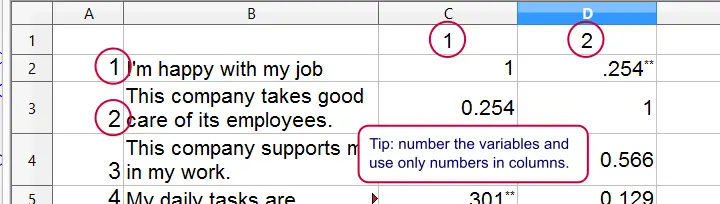
关于相关性,我们希望标记出统计上显著的相关性,但我们不需要它们的样本量或 p 值。由于您无法阻止 SPSS 包含后者,请尝试 SPSS 以 APA 格式显示相关性 (SPSS Correlations in APA Format)。
您可以通过右键单击表格并选择 C opy special  E xcel Worksheet ,在 OpenOffice 或 Excel 电子表格中进一步快速编辑结果。
E xcel Worksheet ,在 OpenOffice 或 Excel 电子表格中进一步快速编辑结果。
参考文献
- Stevens, J. (2002). Applied multivariate statistics for the social sciences. Mahway, NJ: Lawrence Erlbaum Associates.
- Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
- Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Data Analysis. New Jersey: Pearson Prentice Hall.
- Berry, W.D. (1993). Understanding Regression Assumptions. Newbury Park, CA: Sage.
- Field, A. (2013). Discovering Statistics with IBM SPSS Newbury Park, CA: Sage.
- Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
- Nicol, A.M. & Pexman, P.M. (2010). Presenting Your Findings. A Practical Guide for Creating Tables. Washington: APA.