测量尺度 – 是什么以及为什么？

作者：Ruben Geert van den Berg，发表于统计学 A-Z

测量尺度（Measurement Levels）指的是不同类型的变量，这些变量决定了如何对它们进行分析。标准教科书区分了四种这样的测量尺度或变量类型。从低到高，它们分别是：

  1. 定类变量（Nominal Variables）；
  2. 定序变量（Ordinal Variables）；
  3. 定距变量（Interval Variables）；
  4. 定比变量（Ratio Variables）。

测量尺度越高，变量包含的信息就越多。下面的简单流程图展示了如何对变量进行分类。

测量尺度 - 经典方法

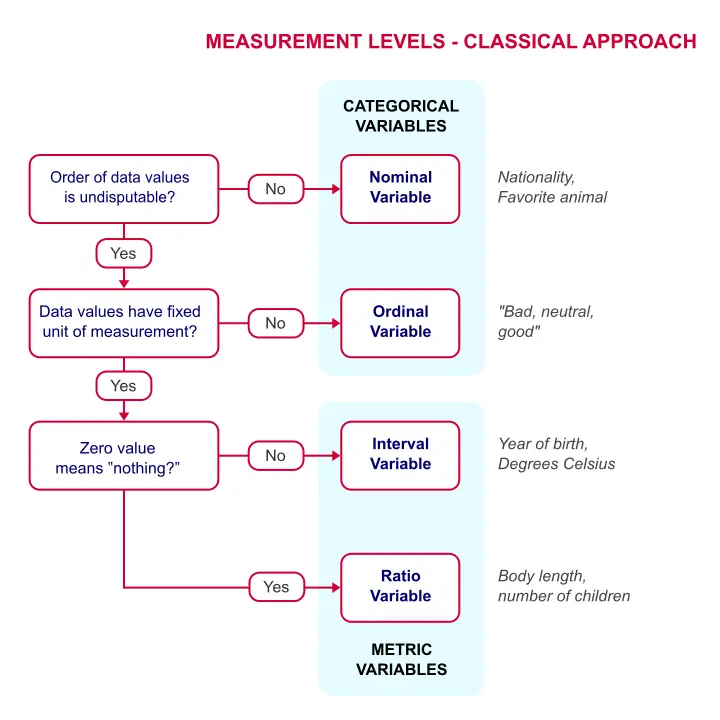测量尺度 测量尺度快速概览

现在让我们通过一些例子来更仔细地了解这些变量类型的真正含义。

定类变量（Nominal Variables）

定类变量是一种变量，其值没有明确的顺序。例如，我们询问受访者他们居住的国家（Country），答案是：

  • 荷兰（the Netherlands）；
  • 比利时（Belgium）；
  • 法国（France）；
  • 德国（Germany）；
  • 卢森堡（Luxembourg）。

那么这些国家的正确顺序是什么？ 我们可以按字母顺序、大小或居民人数对其进行排序。 对于国家/地区的列表，不同的顺序是有意义的。 简而言之，国家/地区没有明确的顺序，因此“国家/地区”是一个定类变量。 现在，在 SPSS 或其他一些数据格式中，国家/地区可以用数字表示（1 = 荷兰，2 = 比利时等等）。 这些数字_确实_有一个明确的顺序。 但国家/地区仍然是一个定类变量，因为这些数字_所代表的_东西——国家/地区——没有明确的顺序。

定类变量的频率分布示例 国家/地区——即使表示为数字——仍然是一个定类变量

类似地，邮政编码（ZIP codes）——代表没有明确顺序的地理区域——也是定类的。 但以美元计价的价格（Prices）——代表货币金额——显然有一个明确的顺序，因此不是定类的。

定序变量（Ordinal Variables）

定序变量的值具有明确的顺序，但没有固定的测量单位。 一些固定的测量单位是米、人、美元或秒。 但是，对于诸如“你觉得你的食物怎么样？”之类的问题，_没有_固定的测量单位，答案类别如下：

  1. 差（Bad）；
  2. 中性（Neutral）；
  3. 好（Good）。

有些人可能会争辩说，差 = 1 分，中性 = 2 分，好 = 3 分。 但这只是一个大胆的猜测。 也许我们的受访者觉得中性代表 1.5 或 2.5 分。 下图对此进行了说明。

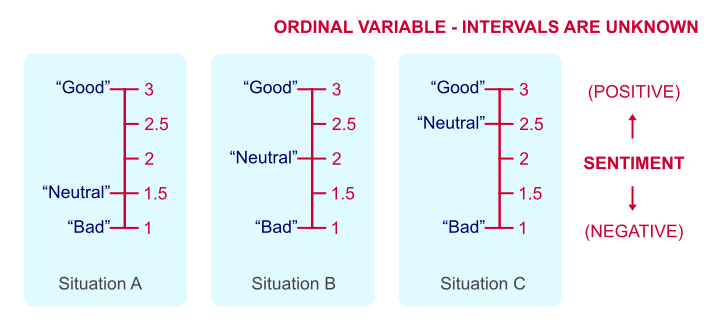定序测量尺度 对于定序变量，答案类别之间的间隔是未知的。

我们无法证明哪种情况是正确的，因为仅仅是“分”不是固定的测量单位。 而且由于我们不知道中性代表 1.5、2 还是 2.5 分，因此对定序变量的计算没有意义。 但是，不那么严格地说，在相等间隔的假设下，对定序变量的计算非常普遍。

另请注意，月收入（Monthly income）衡量为

  1. 少于 1000 欧元（Less than € 1000,-）；
  2. 1000 欧元到 2000 欧元（€ 1000,- to € 2000,-）；
  3. 2000 欧元或以上（€ 2000,- or over）。

是定序的。 欧元是固定的测量单位，但答案是收入类别，而不是欧元的数量。

定距变量（Interval Variables）

定距变量具有固定的测量单位，但零并不意味着“没有”。 一个罕见的例子是“它发生在哪一年（Year）？” 忽略闰日，年份是_时间_的固定测量单位。 但是，零年并不意味着时间方面的“没有”。 因此，乘法对于定距变量没有意义。 2000 年并不比 1000 年“晚两倍”。 摄氏温度也是如此：零度并不意味着温度方面的“没有”。 因此，100 度并不比 50 度热两倍。 然而，对于开尔文温度来说，这个论点_可以_成立。 我们应该补充一点，这是我们能想到的定距变量的仅有的两个例子。 定距变量的分析方式始终与定比变量类似——我们将在下一步讨论。 但将这些区分开来作为单独的测量尺度——所有教科书仍然这样做——是没有意义的。

定比变量（Ratio Variables）

定比变量具有固定的测量单位，零确实意味着“没有”。 一个例子是公斤重量（Weight）。 公斤是一个固定的测量单位，因为它始终代表完全相同的重量。 此外，零公斤对应于重量方面的“没有”。 因此，乘法对于定比变量是有意义的。 事实上，我们只需要一个厨房秤就可以证明 2 倍 1 公斤确实与 1 倍 2 公斤的重量相同。

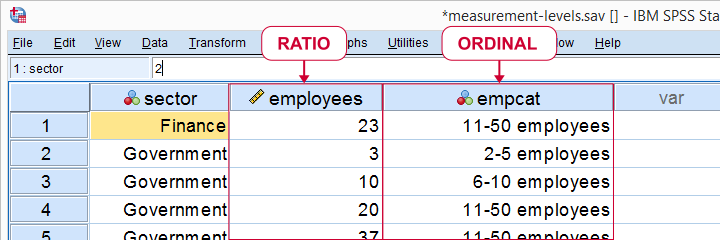以比率和有序级别测量变量的数据 员工人数作为比率以及有序变量

一些教科书提到了“绝对零点”。 我们宁愿避免这种措辞，因为比率变量可能包含负值； 我的银行账户余额可能是负数，但它有一个固定的测量单位——在我的例子中是欧元——并且零意味着“没有”。

经典测量尺度 - 缺点

我们认为测量尺度很重要，因为它们有助于数据分析。 但是，当我们查看常见的统计技术时，我们发现

  • 二分变量与其他所有变量的处理方式不同，但经典测量尺度未能区分它们；
  • 度量变量（定距和定比）的处理方式始终相同；
  • 分类变量（定类和定序）有时以类似方式处理，有时则不然。

由于这些原因，我们认为下面的分类更有帮助。

测量尺度 - 现代方法

定序测量尺度

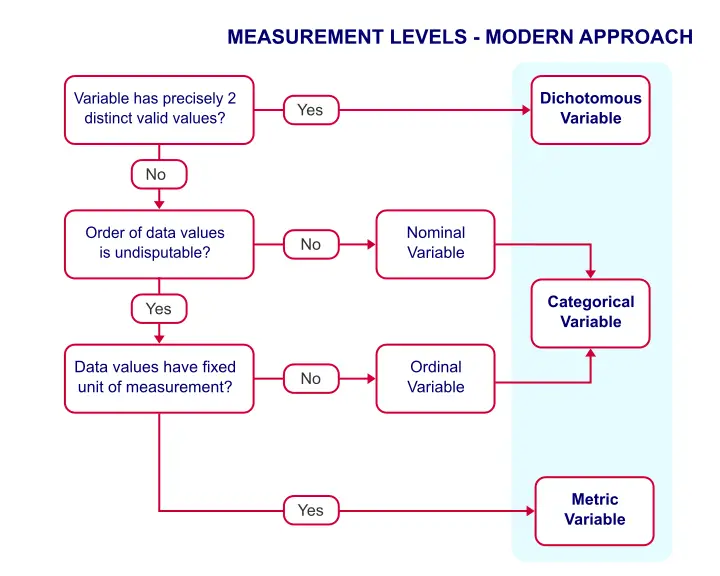
此分类区分了三个主要类别，我们将简要讨论这些类别。

二分变量（Dichotomous Variables）

二分变量只有两个不同的值。 典型的例子是性别（Sex）、拥有汽车（Owning a car）或携带艾滋病毒（Carrying HIV）。 将二分变量区分为单独的测量尺度是有用的，因为它们需要与其他变量不同的分析：

分类变量（Categorical Variables）

分类变量是不能进行有意义计算的变量。 因此，定类变量和定序变量是分类变量。 它们包含（通常很少）答案_类别_。 由于计算没有意义，因此分类变量仅定义组。 因此，我们使用频率分布和条形图分析它们。

度量变量（Metric Variables）

度量变量是可以进行有意义计算的变量。 也就是说：定距变量和定比变量是度量变量。 由于允许进行计算，因此我们通常使用描述性统计信息来分析它们，例如

  • 均值（Means）；
  • 标准差（Standard deviations）；
  • 偏度（Skewnesses）。

数据分析 - 后续步骤

我们刚才论证了

  • 分类变量定义了案例组，并且
  • 我们使用描述性统计信息来分析度量变量。

现在，假设我们想知道两个分类变量是否相关联。 然后，第一个变量定义组，第二个变量定义这些组中的组。 显示此信息的表格是列联表，如下所示。 它基本上包含频率分布中的频率分布

两个分类变量的列联表

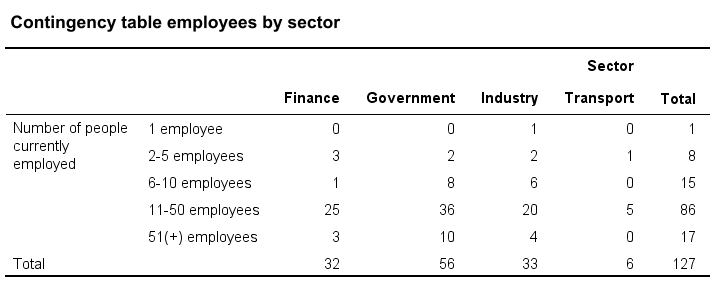
接下来，我们可以使用堆叠条形图可视化关联。 或者，我们可以通过在列联表上运行 卡方独立性检验来检验关联是否具有统计显著性。

或者，也许我们想知道分类变量和度量变量是否相关联。 分类变量定义组。 在这些组中，我们将检查度量变量的描述性统计信息。 因此，我们得到了如下表所示的表格。

按分类变量显示度量变量的描述性统计信息的表格

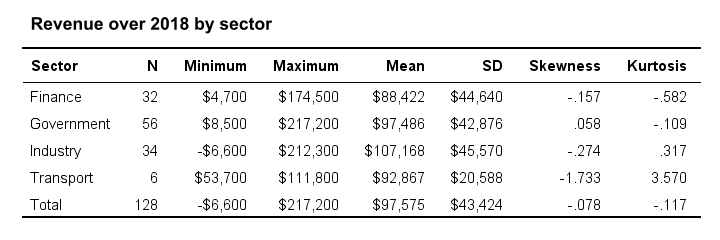
我们可以将均值可视化为按类别显示的均值的条形图。 或者，我们可以使用 ANOVA 检验总体均值是否因类别而异。

现在我们看到了测量尺度如何帮助我们选择正确的分析。 有关按测量尺度进行的分析的更完整概述，请参阅 SPSS 数据分析 - 基本路线图。

感谢阅读！