如何在SPSS中运行Kruskal-Wallis检验？
作者：Ruben Geert van den Berg，发布于非参数检验 
如果单因素方差分析 (one-way ANOVA)的假设不成立，那么Kruskal-Wallis检验 可以作为其替代方法。稍后我们将展示为什么在creatine.sav（本教程中使用的数据）中会出现这种情况。但首先，让我们快速了解一下数据的内容。
快速数据描述
我们的数据包含一项关于肌酸（一种在健美运动员中流行的补剂）的小型实验的结果。参与者被分为3组：一组不服用任何肌酸，另一组在早上服用，还有一组在晚上服用。服用一个月后，测量他们的体重增加量。基本的研究问题是：平均体重增加是否取决于参与者被分配到的肌酸条件？也就是说，我们将检验三个均值（每个均值都基于不同的人群计算）是否相等。对于这种情况，最常用的检验是单因素方差分析，但使用它需要满足一些假设。一些基本的检查将告诉我们，这些假设不满足我们手头的数据。
数据检查 1 - 直方图 (Histogram)
一个非常有效的数据检查方法是在所有计量变量上运行直方图。最快的方法是运行以下语法。
***创建体重增加的直方图。***
frequencies gain
/formats notable
/histogram.直方图结果
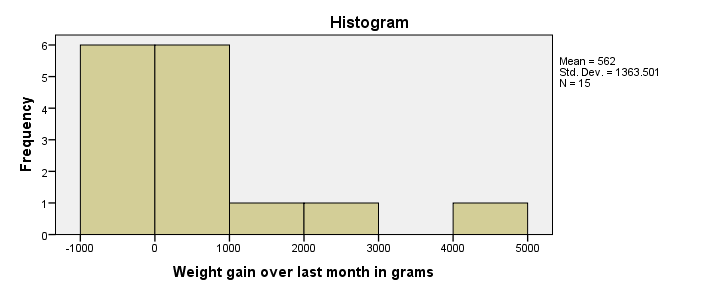
首先，我们的直方图看起来是合理的，所有体重增加量都在-1到+5公斤之间，这在一个月内是合理的结果。但是，我们的结果变量不是正态分布 (normally distributed)，这是ANOVA的要求。对于较大的样本量（例如，每组至少30人），这不是问题。原因是中心极限定理 (central limit theorem)。它基本上指出，对于合理的样本量，均值和总和的抽样分布 (sampling distribution)始终是正态分布的，而与变量的原始分布无关。但是，对于我们手头的小样本来说，这确实构成了一个实际问题。
数据检查 2 - 各组的描述性统计 (Descriptives)
好的，在确保体重增加的结果看起来可信之后，让我们看看我们的3个组是否真的具有不同的均值。最快的方法是使用简单的MEANS命令，如下所示。
***检查均值和标准差。***
means gain by group.SPSS MEANS输出
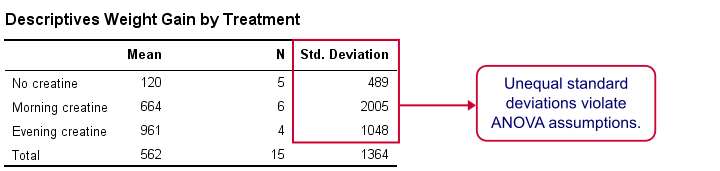
首先，请注意，我们的晚上服用肌酸组（4名参与者）平均体重增加了961克，而“不服用肌酸”组则为120克。这表明肌酸确实会产生实际影响。 但不要忽略我们各组的标准差：它们非常不同，但ANOVA要求它们相等。所有组的总体标准差相等的假设被称为同方差性 (homoscedasticity)。这是第二次违反ANOVA假设。
Kruskal-Wallis 检验
那么我们现在应该怎么办？我们想使用ANOVA，但我们的数据严重违反了其假设。好吧，专门为此情况设计的检验是Kruskal-Wallis检验，它不需要这些假设。它基本上用它们的秩次替换体重增加分数，并检验这些秩次在各组之间是否相等。我们将按照下面的屏幕截图运行它。
在SPSS中运行Kruskal-Wallis检验
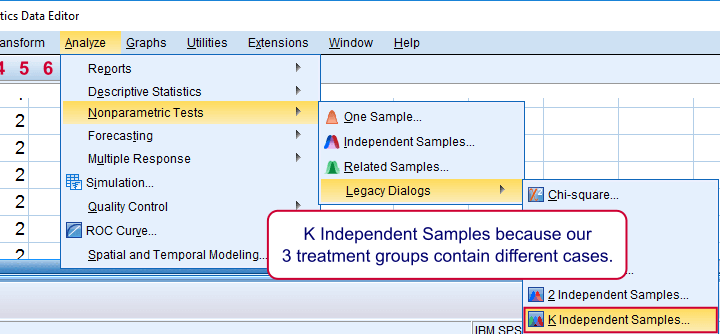
如果我们比较3个或更多组的个案，则使用 “K 个独立样本 (K Independent Samples)”。它们是“独立的”，因为我们的组不重叠（每个个案仅属于一种肌酸条件）。
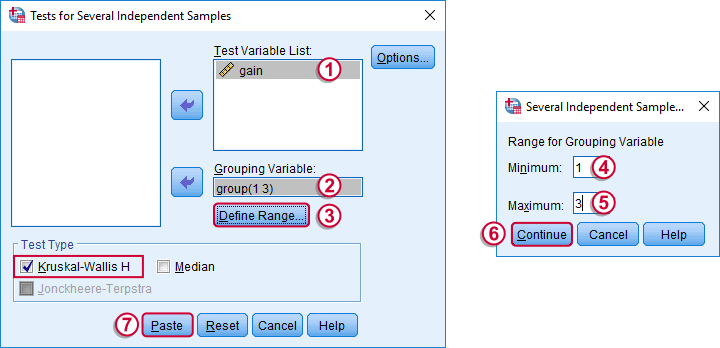
根据您的许可证，您的SPSS版本可能具有或不具有下面显示的“精确 (Exact)”选项。如果不是，跳过此步骤即可。
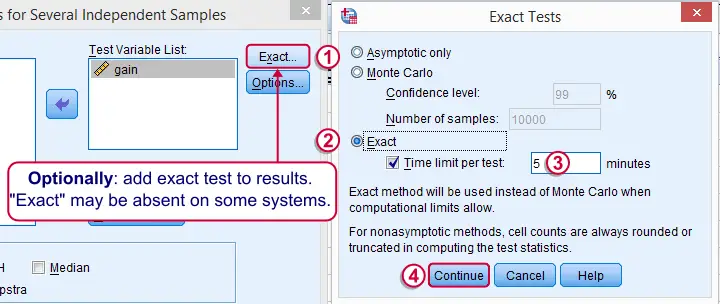
SPSS Kruskal-Wallis 检验语法
按照之前的屏幕截图操作，会得到以下语法。我们将运行它并解释输出。
***基本的 Kruskal-Wallis 检验语法。***
NPAR TESTS
/K-W=gain BY group(1 3)
/MISSING ANALYSIS.SPSS Kruskal-Wallis 检验输出
我们将跳过“秩 (RANKS)”表，直接进入下面显示的“检验统计量 (Test Statistics)”。
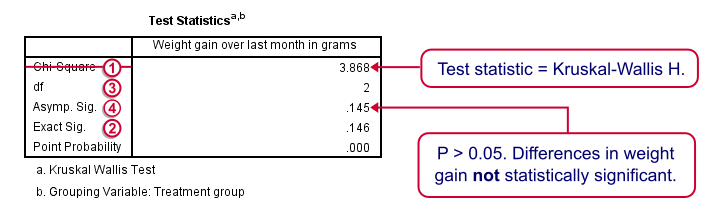
我们的检验统计量（被SPSS错误地标记为“卡方 (Chi-Square)”）被称为 Kruskal-Wallis H。值越大，表明我们比较的组之间的差异越大。对于我们的数据，它大约为 3.87。我们需要知道它的抽样分布 (sampling distribution)，以评估这个值是否异常大。 
精确显著性 (Exact Sig.) 使用 H 的精确（但非常复杂）的抽样分布。但是，事实证明，如果每个组包含 4 个或更多个案，则此精确抽样分布几乎与（更简单的）卡方分布相同。 
因此，我们通常使用卡方分布来近似 p值 (p-value)。如果我们比较 k 个组，则我们有 k - 1 个自由度，在我们的输出中用 df 表示。 
渐近显著性 (Asymp. Sig.) 是基于我们的卡方近似的 p 值。 0.145 的值基本上意味着，如果肌酸在整个人群中没有任何影响，那么我们有 14.5% 的机会找到我们的样本结果。因此，如果肌酸没有任何作用，我们有相当大的（14.5%）机会仅仅因为随机抽样而发现如此微小的体重增加差异。如果 p > 0.05，我们通常得出结论，我们的差异在统计上不显著。 请注意，我们的精确 p 值为 0.146，而近似 p 值为 0.145。这支持了 H 几乎完美地服从卡方分布的说法。
Kruskal-Wallis 检验 - 报告
报告我们的检验结果的官方方式包括我们的卡方值、df 和 p，如“这项研究未证明肌酸有任何作用，H(2) = 3.87，p = 0.15”。