本篇文章介绍了两种判断离群值的方法,以及如何使用SPSS进行操作, 并且找到离群值之后的处理方法。推荐第二种方法。
均值和标准差标准
离群值(outlier)指的是偏离变量均值太多的数据, 那么偏离多少算多呢? 一般我们的判断标准是3个标准差, 因为如果数据符合正态分布(这是最常用的也是大多数统计算法要求的分布), 某个数据里均值偏离3个标准差就意味着这个数据出现的概率小于0.01, 已经是很小了, 不能代表数据整理的规律, 所以应当将其排除。
因此离群值的范围就是: 大于M+3SD或者小于M-3SD
SPSS操作
依次点击菜单中: 分析–>描述统计–>描述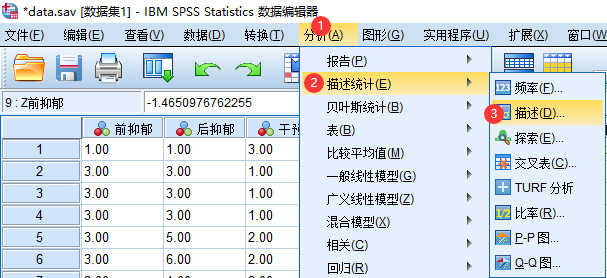
记得勾选计算Z分数的选项:
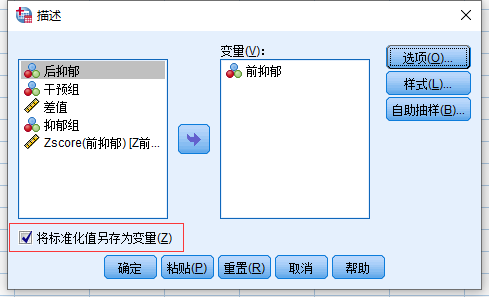
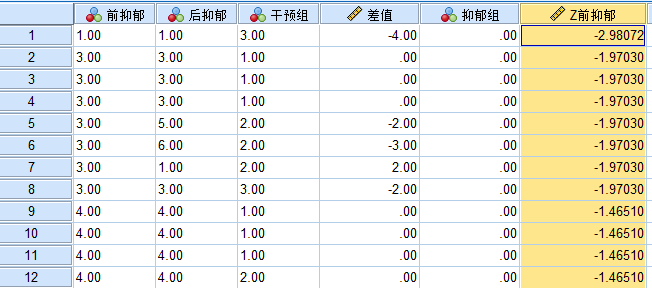
最后你会在数据中看到, 多了一个变量”Z前抑郁”, 这就是我们需要的Z分数, 我们升序或者降序排列这个变量, 就能在最上面和下面找到离群值, 如果有绝对值超过3的数据, 就可以认为是离群值

显然我们没有离群值:
百分位数标准
离群值(outlier)指的是偏离大部分数据的值, 大部分数据我们用25%和75%的分位数来判断, 也就是说将数据从小到大排列, 位于25%和75%中间的数据为大多数数据, 因此离群值的范围就是:
- 大于75分位数1.5个interquartile
- 小于25分位数1.5个interquartile
interquartile = 75分位数-25分位数
spss操作
依次点击菜单中: 分析–>描述统计–>探索

将”前抑郁”和”后抑郁”这两个变量放入到因变量列表
在”统计”对话框中, 勾选”百分位数”
结果解读
在百分位数表中, 我们可以看到从”5”到”95”分位数, 那么”图基枢纽(Tukey’s Hinges)”是啥?翻译的很烂
Tukey’s Hinges一种矫正的计算分位数的方法, 更科学。
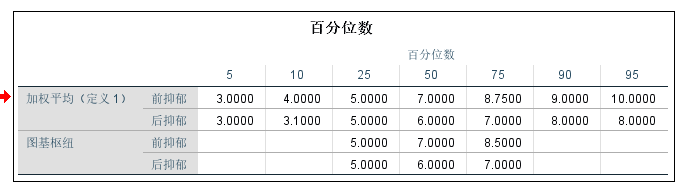
根据上表, 我们可以计算两个变量的离群值的范围:
前抑郁
- 超过8.5+1.5*(8.5-5)=13.75
- 低于5-1.5*(8.5-5)=3.25
后抑郁
- 超过7+1.5*(7-5)=10
- 低于5-1.5*(7-5)=2
SPSS自动为我们输出了箱式图,上下边缘超过1.5倍箱式长度为离群值, 这个范围就是上面我们计算的范围, 对于前抑郁, 没有看到离群值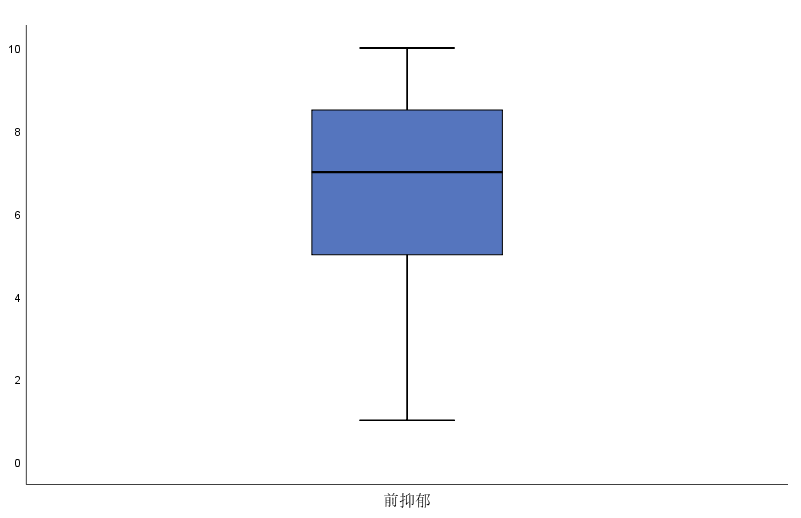
对于后抑郁, 输出了三个离群值, 这三个值紧挨在一起, 所以看起来像是一个, 不过, 图中标出了三个数值所在行数:1, 7, 23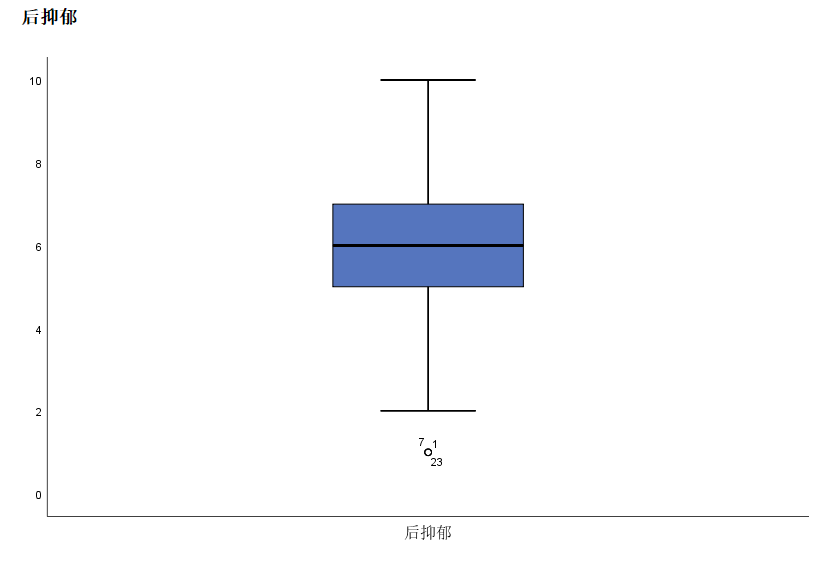
假如我们对后抑郁进行降序排序, 你会发现行数改了, 只输出了两个, 因为139其实是位于138和140之间的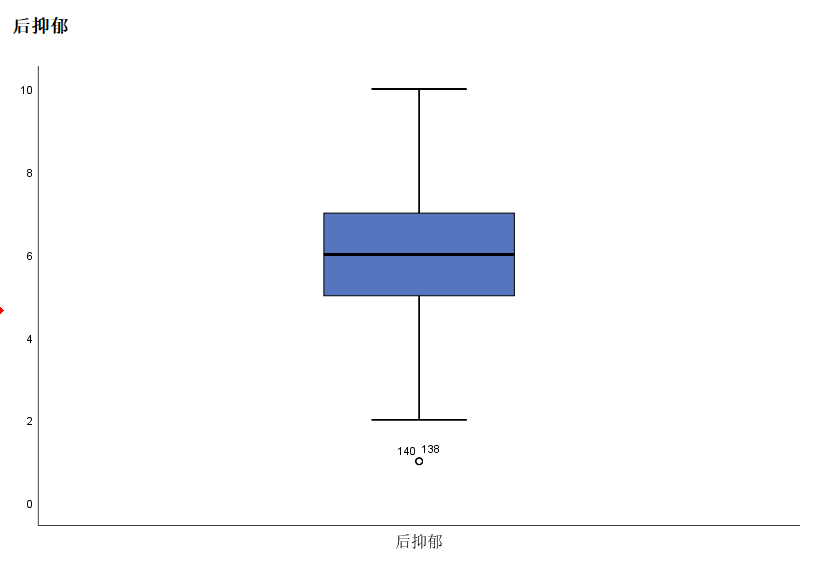
这是排序后的数据:
如果用均值标准差的标准来判断, 这三个离群值其实没有超出三个标准差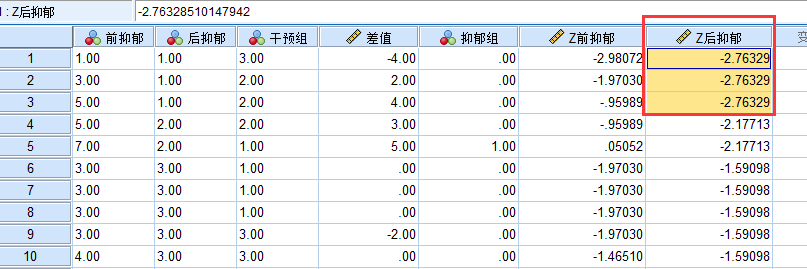
分组离群值
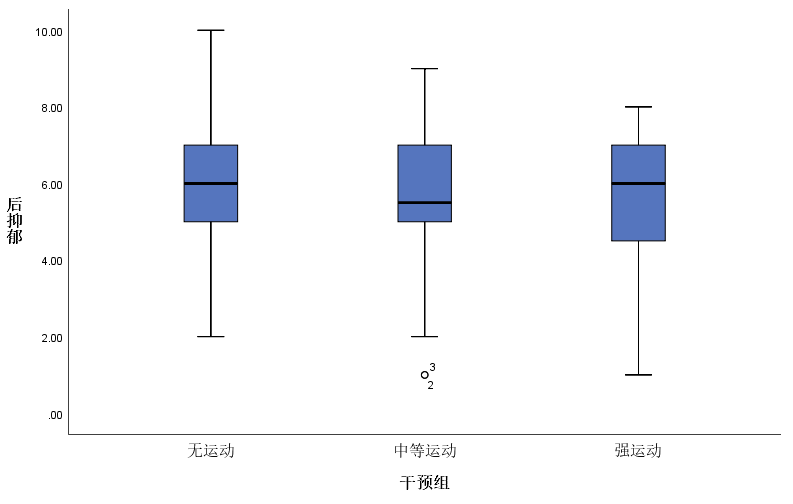
很多情况下, 我们需要判断数据在某个分组内是否属于离群值, 比如我们的数据中有一个变量是”干预组”, 分为三组, 在三组内, 我们分别去看”后抑郁”有没有离群值, 因此我们可以将”干预组”放到因子列表中

最后箱式图会出现三个组, 这样我们就可以分别判断各组的离群值了
出现离群值的处理方法
- 数据量足够的话就删掉离群值
- 用附近最近的数据替换
参考文献
- 解释Tukey’s Hinges: https://www.statisticshowto.com/upper-hinge-lower-hinge/
视频教程
注意
本文由jupyter notebook转换而来, 您可以在这里下载notebook
统计咨询请加QQ 2726725926, 微信 mllncn, SPSS统计咨询是收费的
微博上@mlln-cn可以向我免费题问
请记住我的网址: mlln.cn 或者 jupyter.cn


