使用潜变量混合增长模型（GMM）实用指南

本教程旨在为研究人员提供一个关于如何使用混合增长模型（GMM）进行纵向数据分析的实践指南。GMM 是一种用于识别多个未观察到的亚群体，描述每个亚群体内的纵向变化，并检查这些亚群体之间变化差异的方法。本教程将涵盖 GMM 的基本概念、四步分析方法以及使用 Mplus 软件进行模型估计和选择的示例。

混合增长模型（GMM）简介

混合增长模型（GMM）是一种统计技术，用于识别纵向数据中存在的不同的潜在群体。传统的生长曲线模型假设所有个体都来自一个具有相同参数集的群体，而 GMM 则允许存在多个具有不同生长模式的未观察到的亚群体。GMM 可以被视为多组生长模型的扩展，其中分组变量是潜在的或未观察到的。

GMM 的目标是识别数据中可能的亚组，并描述这些未观察到的组之间和内部的纵向变化差异。该方法估计每个个体属于每个组/类的概率，以及每个未观察到的组的平均变化、变化中的个体间差异程度和变化模式。

GMM 的四个步骤

本教程将概述进行 GMM 分析的四步方法：

1. 问题定义： 明确研究问题，制定 GMM 假设，并获得基线单组增长曲线模型。
2. 模型设定： 设定一系列模型，以检验未观察到的组在平均变化、变化中的个体间差异程度和变化模式方面的差异。
3. 模型估计： 使用最大似然（ML）或贝叶斯方法估计模型参数和个体后验概率。
4. 模型选择与解释： 使用各种拟合指标、理论和先前研究结果来确定哪个模型最能代表观察到的数据。

示例数据

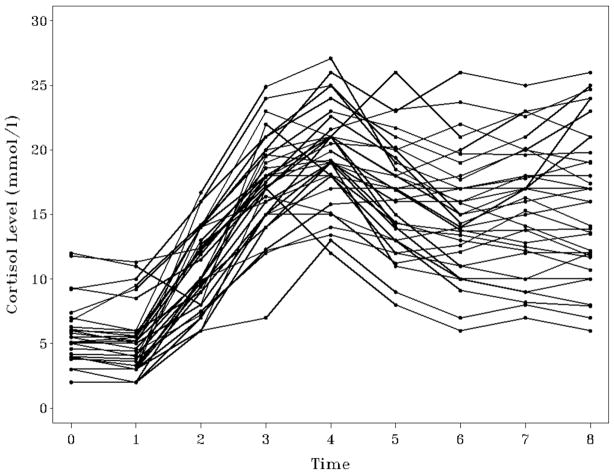
本教程使用的数据来自 MacArthur 成功老龄化研究，该研究调查了个体在应对压力刺激时的皮质醇产生和扩散的时间过程中的个体间差异。从 34 位老年参与者在几个小时内连续 9 次测量皮质醇 (mmol/l)。前两次测量（t = 0 和 1）作为基线测量，之后个体开始驾驶模拟挑战任务。观察 2、3 和 4 在挑战期间和挑战后直接进行，是皮质醇产生或反应的指标。剩余的观察（5、6、7 和 8）在挑战后休息期间进行，并被视为皮质醇消散的指标。

数据集的特点是非线性的个体内部变化和这些变化中的个体间差异。GMM 的目标是确定是否存在表现出不同变化模式的未观察到的个体亚组。如图 2 所示：

步骤 1：问题定义

第一步是明确研究问题并制定关于未观察到的组的假设。在本例中，研究问题是“是否存在多种皮质醇应激反应表型？”基于先前研究，我们假设数据中存在两个亚组：“典型”个体，他们在暴露于压力后不久表现出皮质醇水平的下调，以及“慢性应激”个体，由于一生中长期暴露于应激，他们在暴露于压力后不表现出下调。

步骤 2：模型设定

模型设定涉及设定一系列模型，以检验未观察到的组在平均变化、变化中的个体间差异程度和变化模式方面的差异。从基线模型 1-ClassBaseline 开始，我们设定模型来检验两个未观察到的组可能如何不同，例如 2-ClassMeans、2-ClassMeans+Covs 和 2-ClassMeans+Covs+Pattern。我们还设定了具有三个未观察到的组的模型：3-ClassMeans、3-ClassMeans+Covs 和 3-ClassMeans+Covs+Pattern。

步骤 3：模型估计

使用 Mplus 5.0（Muthén & Muthén, 1998–2008）中的期望最大化（EM）估计程序，将上述模型组拟合到示例数据。报告所有七个模型的拟合统计数据（如表 1 所示）。Mplus 程序代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

TITLE: Latent Basis 2-Class Growth Mixture Model – Means+Cov+Pattern; 
DATA: FILE= data.dat; 
VARIABLE: NAMES = t1-t9; 
USEVAR= t1-t9; 
CLASSES = c(2); 
ANALYSIS: TYPE= MIXTURE; 
MODEL: 
%OVERALL% 
!Intercept Loadings 
g0 BY t1-t9@1; !Latent Basis Slope Loadings 
g1 BY t1@0.0 t2* (L2) t3* (L3) t4* (L4) t5@1.0 t6* (L6) t7* (L7) t8* (L8) t9* (L9); 
!Intercept & Slope Means, Manifest Means fixed to Zero 
[g0*0] (M0); [g1*2] (M1); [t1-t9@0]; 
!Intercept & Slope Variances & Covariances, Residual Variances 
g0*5 (V0); g1*5 (V1); g0 WITH g1*0 (C01); t1-t9*20 (Ve1); 
!Class 1 Model Statement 
%c#1% [g0*3 g1*5]; g0 g1; g0 WITH g1; g1 BY t1@.0 t2*.0 t3*.5 t4*.8 t5@1.0 t6*.8 t7*.6 t8*.4 t9*.4; 
!Class 2 Model Statement 
%c#2% [g0*5 g1*15]; g0 g1; g0 WITH g1; g1 BY t1@.0 t2*.0 t3*.5 t4*.8 t5@1.0 t6*1.0 t7*1.0 t8*1.0 t9*1.0; 
OUTPUT: STANDARDIZED TECH7 TECH11 TECH14;

步骤 4：模型选择和解释

模型选择的目标是确定哪个模型最能代表观察到的数据。本教程提供了可用于做出决策的几种类型的模型评估：

• 评估估计输出：识别参数估计中的任何问题
• 信息标准：检查AIC, BIC, ABIC值
• 熵：熵值越高，类分离越好，值大于0.8表示类之间分离良好。
• 似然比检验： 使用 Vuong-Lo-Mendell-Rubin 似然比检验 (VLMR-LRT) 和调整后的 Lo-Mendell-Rubin 似然比检验 (Adjusted LRT) 来比较具有不同类别数的模型。
  对估计参数和模型输出做评估, 如表 1 所示。

在本例中，基于拟合统计数据和理论考虑，选择 2-ClassMeans+Covs+Pattern 模型作为最合适的模型。

表 2 显示了2-ClassMeans+Covs+Pattern 模型的估计参数。

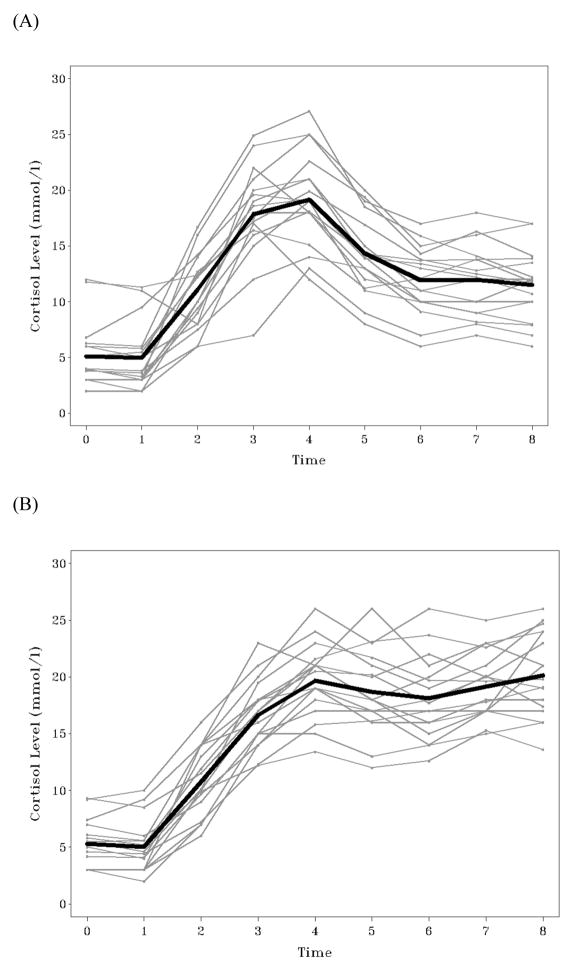
图 3 显示了基于最可能的类成员和每个类的平均趋势绘制的个体。

警告

GMM 是一种约束性探索技术，模型结果可能会受到模型规范期间施加的特定界限的限制。存在发现和识别错误组的实际危险。因此，必须确保估计值和类别数量有意义。我们建议通过使用新数据复制结果并确认潜在分组变量以可预测的方式与其他测量变量相关来获得进一步的证据，证明这些组是真实的。

资源下载

本教程仅列出了1个模型的mplus代码, 如果想要所有模型的代码以及mplus输出结果, 可以访问这里: https://t.zsxq.com/ChraU