元 分析如此有用的原因之一是，它可以将几个不精确的发现组合成一个更精确的发现。在大多数情况下，元分析产生的估计值比任何纳入的研究都具有更窄的置信区间。当真实效应较小时，这尤其有用。虽然初步研究可能无法确定小效应的显著性，但元分析估计通常可以提供验证这种小效应存在所需的统计功效。
然而，统计功效的缺乏可能仍然起着重要的作用——即使在元分析中也是如此。许多元分析中纳入的研究数量很少，通常低于\(K=\) 10。例如，Cochrane 系统评价中的研究数量中位数为 6 个 [@borenstein2011introduction]。如果我们考虑到元分析通常包括亚组分析和元回归，这需要更大的功效，那么这个问题就变得更加严重。此外，许多元分析显示出较高的研究间异质性。这也降低了整体精度，从而降低了统计功效。
我们已经在第 @ref(p-curve-es) 章中讨论了统计功效的概念，在那里我们了解了 p 曲线方法。统计功效背后的思想源于经典假设检验。它与假设检验中可能发生的两种类型的错误直接相关。第一个错误是接受备择假设（例如，\(\mu_1 \neq \mu_2\)），而原假设 (\(\mu_1 = \mu_2\)) 是正确的。这会导致假阳性，也称为 Type I 或 \(\alpha\) 错误。相反，我们也有可能接受原假设，而备择假设是正确的。这会产生假阴性，称为 Type II 或 \(\beta\) 错误。
检验的功效直接取决于 \(\beta\)。它被定义为功效 = \(1 - \beta\)。假设我们的原假设表明两组均值之间没有差异，而备择假设假定存在差异（即“效应”）。统计功效可以定义为检验将检测到效应（即均值差异）的概率，如果它存在：
\[\begin{equation} \text{功效} = P(\text{拒绝 H}_0~|~\mu_1 \neq \mu_2) = 1 - \beta (\#eq:pow1) \end{equation}\]
通常的做法是假设 I 类错误比 II 类错误更严重。因此，\(\alpha\) 水平通常设置为 0.05，\(\beta\) 水平设置为 0.2。这导致了一个阈值 \(1-\beta\) = 1 - 0.2 = 80%，通常用于确定检验的统计功效是否足够。当研究人员计划一项新的研究时，他们通常选择一个保证 80% 功效的样本量。当真实效应较大时，更容易获得具有统计显著性的结果。因此，当功效固定为 80% 时，所需的样本量仅取决于真实效应的大小。假设的效应越小，确定 80% 功效所需的样本量就越大。
进行初步研究的研究人员可以根据他们期望发现的效应大小先验地计划他们的样本量。在元分析中，情况有所不同，我们只能使用已发表的材料。但是，我们可以控制纳入元分析的研究的数量和类型（例如，通过定义更宽松或更严格的纳入标准）。通过这种方式，我们也可以调整整体功效。有几个因素会影响元分析中的统计功效：
纳入或符合条件的研究的总数及其样本量。我们期望有多少研究，它们是相当小还是大？
我们想要找到的效应大小。这一点尤为重要，因为我们必须假设效应大小必须有多大才能仍然有意义。例如，一项研究计算出，对于抑郁症干预措施，即使像 SMD = 0.24 这样小的效应也可能对患者有意义 [@cuijpers2014threshold]。如果我们想研究干预措施的负面影响（例如死亡或症状恶化），即使是非常小的效应大小也是极其重要的，应该被检测到。
预期的研究间异质性。大量的异质性会影响我们元分析估计的精度，从而影响我们发现显著效应的潜力。
除此之外，考虑我们想要进行的其他分析也很重要，例如亚组分析。每个亚组有多少研究？我们想在每个组中找到什么效应？
事后功效检验：“滥用权力”
请注意，功效分析应始终先验地进行，这意味着在您执行元分析之前。
在分析之后进行 (“事后”) 的功效分析基于一个有严重缺陷的逻辑 [@hoenig2001abuse]。首先，事后功效分析是无信息的——它告诉我们的东西我们已经知道了。当我们发现基于我们收集的样本，效应不显著时，计算出的事后功效将根据定义是不充分的（即 50% 或更低）。当我们计算一个检验的事后功效时，我们只是“玩弄”一个直接链接到结果的 (p) 值的功效函数。
事后功效估计中没有任何 (p) 值不会告诉我们的东西。也就是说，基于我们检验的效应和样本量，功效不足以确定统计显著性。
当我们解释事后功效时，这也可能导致功效方法悖论 (PAP)。当 p 值较小时，认为产生没有显著效应的分析显示出更多证据表明原假设是正确的，因为那时，检测真实效应的功效会更高，从而产生这种悖论。
要确定固定效应模型下元分析的功效，我们必须指定一个分布，该分布表示我们的备择假设是正确的。然而，要做到这一点，简单地说 \(\theta \neq 0\)（即存在某种效应）是不够的。我们必须假设一个特定的真实效应，我们希望能够以足够的（80%）功效检测到该效应。例如 SMD = 0.29。
我们之前已经介绍过（参见第 @ref(metareg-continuous) 章），将效应大小除以其标准误差会创建一个 \(z\) 分数。这些 \(z\) 分数遵循标准正态分布，其中 \(|z| \geq\) 1.96 的值表示该效应与零显著不同 (\(p<\) 0.05)。这正是我们想要在元分析中实现的：无论我们结果的精确效应大小和标准误差有多大，值 \(|z|\) 都应该至少为 1.96，因此具有统计显著性：
\[\begin{equation} z = \frac{\theta}{\sigma_{\theta}}~~~\text{其中}~~~|z| \geq 1.96。 (\#eq:pow2) \end{equation}\]
\(\sigma_{\theta}\) 的值，即合并效应大小的标准误差，可以使用以下公式计算：
\[\begin{equation} \sigma_{\theta}=\sqrt{\frac{\left(\frac{n_1+n_2}{n_1n_2}\right)+\left(\frac{\theta^2}{2(n_1+n_2)}\right)}{K}} (\#eq:pow3) \end{equation}\]
其中 \(n_1\) 和 \(n_2\) 代表研究中第 1 组和第 2 组的样本量，其中 \(\theta\) 是假设的效应大小（表示为标准化均值差），\(K\) 是元分析中研究的总数。重要的是，作为简化，此公式假设所有纳入研究中两组的样本量都是相同的。
该公式与用于计算标准化均值差的标准误差的公式非常相似，但有一个例外。我们现在将标准误差除以 \(K\)。这意味着我们合并效应的标准误差减少了 \(K\) 倍，代表元分析中研究的总数。换句话说，当假设一个固定效应模型时，合并研究会导致我们整体效应的精度提高 \(K\) 倍1。
在我们定义了 \(\theta\) 并计算出 \(\sigma_{\theta}\) 之后，我们最终会得到一个 \(z\) 值。给定组大小为 \(n_1\) 和 \(n_2\) 的 \(K\) 项研究的数量，可以使用此 \(z\) 分数来获得元分析的功效：
\[\begin{align} \text{功效} &= 1-\beta \notag \\ &= 1-\Phi(c_{\alpha}-z)+\Phi(-c_{\alpha}-z) \notag \\ &= 1-\Phi(1.96-z)+\Phi(-1.96-z)。 (\#eq:pow4) \end{align}\]
其中 \(c_{\alpha}\) 是标准正态分布的临界值，给定指定的 \(\alpha\) 水平。符号 \(\Phi\) 代表标准正态分布的累积分布函数 (CDF)，\(\Phi(z)\)。在 R 中，标准正态分布的 CDF 在 pnorm 函数中实现。
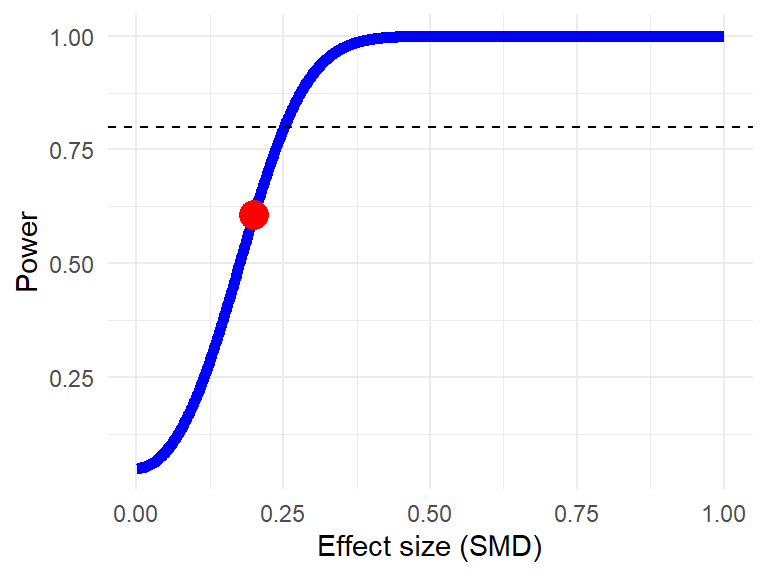
我们现在可以使用这些公式来计算固定效应元分析的功效。想象一下，我们期望有 \(K=\) 10 项研究，每项研究中两组大约有 25 名参与者。我们希望能够检测到 SMD = 0.2 的效应。这样的元分析有什么功效？
# 定义假设
theta <- 0.2
K <- 10
n1 <- 25
n2 <- 25
# 计算合并效应标准误差
sigma <- sqrt(((n1+n2)/(n1*n2)+(theta^2/(2*n1+n2)))/K)
# 计算 z
z = theta/sigma
# 计算功效
1 - pnorm(1.96-z) + pnorm(-1.96-z)[1] 0.6059151我们看到，即使纳入了 10 项研究，这样的元分析也只有 60.6% 的功效，因此功效不足。计算（固定效应）元分析功效的更方便的方法是使用 power.analysis 函数。
power.analysis 函数包含以下参数：
d。假设的或合理的总体效应大小，表示为标准化均值差 (SMD)。效应大小必须是正数值。
OR。与对照组相比，治疗或干预的假设效应，表示为优势比 (OR)。如果同时指定了 d 和 OR，则只会计算 d 值的输出。
k。元分析中预期的研究数量。
n1、n2。纳入研究中第 1 组和第 2 组的预期平均样本量。
p。要使用的 alpha 水平。默认值为 \(\alpha\)=0.05。
heterogeneity。研究间异质性的水平。可以为 "fixed" 表示没有异质性（固定效应模型），"low" 表示低异质性，"moderate" 表示中等大小的异质性，或 "high" 表示高水平的异质性。默认为 "fixed"。
让我们使用与之前示例中相同的输入来尝试一下这个函数。
library(dmetar)
power.analysis(d = 0.2,
k = 10,
n1 = 25,
n2 = 25,
p = 0.05)Fixed-effect model used. 
Power: 60.66%对于假设随机效应模型的功效分析，我们必须考虑研究间异质性方差 \(\tau^2\)。因此，我们需要计算标准误差的调整版本，\(\sigma^*_{\theta}\):
\[\begin{equation} \sigma^*_{\theta}=\sqrt{\frac{\left(\frac{n_1+n_2}{n_1n_2}\right)+\left(\frac{\theta^2}{2(n_1+n_2)}\right)+\tau^2}{K}} (\#eq:pow5) \end{equation}\]
问题是 \(\tau^2\) 的值通常在看到数据之前是未知的。然而，Hedges 和 Pigott [-@hedges2001power] 提供了可用于模拟低、中或大研究间异质性的指南：
低异质性：
\[\begin{equation} \sigma^*_{\theta} = \sqrt{1.33\times\dfrac{\sigma^2_{\theta}}{K}} (\#eq:pow6) \end{equation}\]
中等异质性：
\[\begin{equation} \sigma^*_{\theta} = \sqrt{1.67\times\dfrac{\sigma^2_{\theta}}{K}} (\#eq:pow7) \end{equation}\]
高异质性：
\[\begin{equation} \sigma^*_{\theta} = \sqrt{2\times\dfrac{\sigma^2_{\theta}}{K}} (\#eq:pow8) \end{equation}\]
power.analysis 函数也可以用于随机效应元分析。可以使用 heterogeneity 参数控制假设的研究间异质性的量。可能的值为 "low"、"moderate" 和 "high"。使用与前面示例中相同的值，我们现在计算一下当研究间异质性为中等时，预期的功效。
power.analysis(d = 0.2,
k = 10,
n1 = 25,
n2 = 25,
p = 0.05,
heterogeneity = "moderate")## 使用了随机效应模型（假设中等异质性）。
## 功效：40.76%我们看到估计的功效为 40.76%。这低于规范的 80% 阈值。这也低于我们假设固定效应模型时获得的 60.66%。这是因为研究间异质性降低了我们合并效应估计的精度，导致统计功效下降。
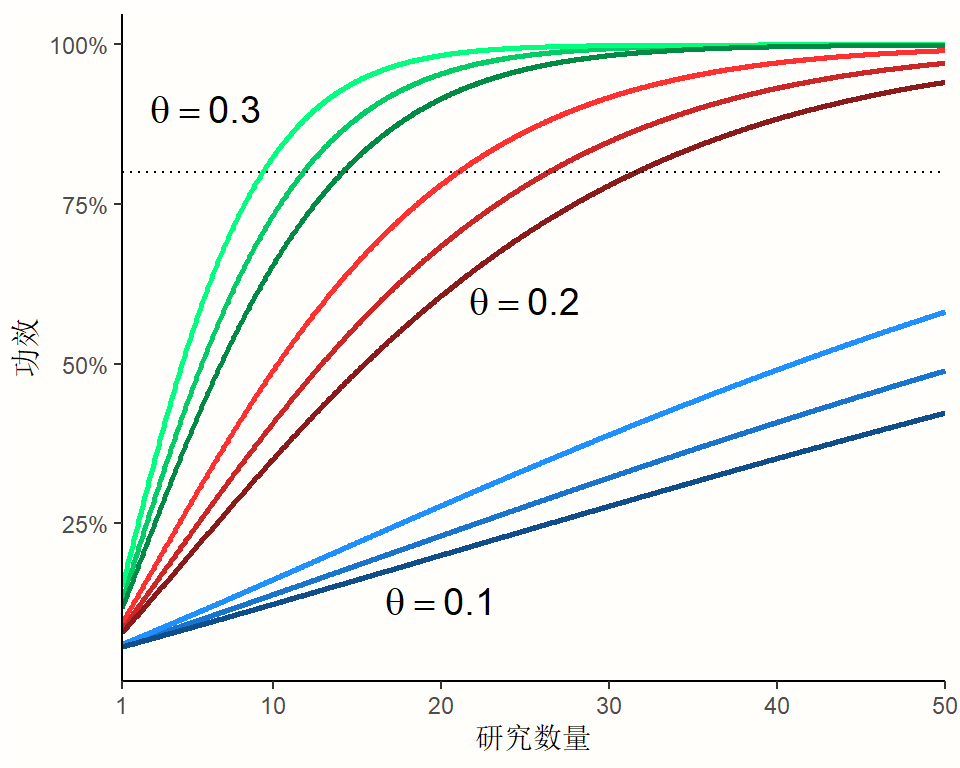
图 @ref(fig:power) 可视化了真实效应大小、研究数量和研究间异质性量对元分析功效的影响。2
在计划亚组分析时，了解两组之间的差异必须有多大，以便我们可以在我们可用的研究数量下检测到它，这可能是有意义的。这就是亚组差异的功效分析可以应用的地方。可以使用 power.analysis.subgroup 函数在 R 中进行亚组功效分析，该函数实现了 Hedges 和 Pigott [-@hedges2004power] 描述的方法。
让我们假设我们期望第一组显示 SMD = 0.3 的效应，标准误差为 0.13，而第二组具有 SMD = 0.66 的效应，标准误差为 0.14。我们可以将这些假设作为输入来调用我们的函数：
# 加载当前目录下的 power.analysis.subgroup.R 文件
source("power.analysis.subgroup.R")
power.analysis.subgroup(TE1 = 0.30, TE2 = 0.66,
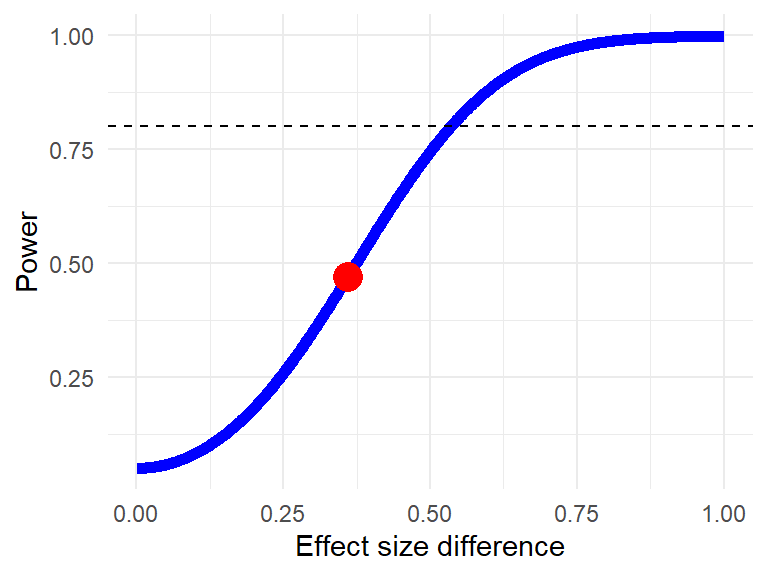
seTE1 = 0.13, seTE2 = 0.14)Minimum effect size difference needed for sufficient power: 0.536 (input: 0.36)
Power for subgroup difference test (two-tailed): 46.99%
在输出中，我们可以看到我们想象的亚组检验的功效 (47%) 将不足够。输出还告诉我们，在所有条件相同的情况下，效应大小差异需要至少为 0.54 才能达到足够的功效。
\[\tag*{$\blacksquare$}\]