子组分析

在 第 @ref(heterogeneity) 章中,我们讨论了研究间异质性的概念,以及它在元分析中的重要性。我们还学习了一些方法,允许我们识别哪些研究对观察到的异质性有贡献,作为离群值和影响分析的一部分。在这些分析中,我们从纯粹的统计角度来处理我们的元分析。我们“测量”数据中相当大的异质性,因此排除具有不合适的统计属性(即,离群和有影响的研究)的研究,以提高我们模型的稳健性。
这种方法可以被看作是事后程序。离群值和影响分析是在看到数据之后进行的,而且通常是因为我们发现的结果。此外,它们除了数据本身之外,不关注任何其他东西。一个影响分析方法可能会告诉我们,某些研究没有正确地遵循我们模型的预期,但没有告诉我们为什么会这样。这可能是因为这项研究使用了稍微不同的研究方法或治疗方法。然而,我们无法仅凭这项研究的影响来了解这一点。
想象一下,你进行了一项元分析,调查一种医疗手段的有效性。你发现,总的来说,这种治疗方法没有效果。然而,有三项研究发现了相当大的治疗效果。有可能在影响分析中检测到这些研究,但这不会告诉你它们为什么有影响力。有可能是这三项研究都使用了一种与所有其他研究略有不同的治疗方法,而这个小细节对治疗的有效性产生了深远的影响。这将是一个开创性的发现。然而,这仅仅通过离群值和影响分析是无法实现的。
这清楚地表明,我们需要一种不同的方法,一种可以让我们识别为什么在我们的数据中可以找到特定的异质性模式的方法。子组分析,也称为调节效应分析,是做到这一点的一种方法。它们允许我们测试具体的假设,描述为什么某些类型的研究产生比其他研究更低或更高的效果。
正如我们在第 @ref(analysis-plan) 章中学到的,子组测试应该先验定义。在我们开始进行元分析之前,我们应该定义可能影响观察到的效应量的不同研究特征,并相应地对每项研究进行编码。效应量可能不同的原因有很多,但我们应该将自己限制在与我们的分析相关的那些原因上。
例如,我们可以检查某种类型的药物是否比另一种药物产生更高的效果。或者,我们可以将随访期较短的研究与随访期较长的研究进行比较。我们还可以检查观察到的效果是否因研究进行的文化区域而异。作为一名元分析师,拥有一些特定领域的专业知识会有所帮助,因为这可以让你找到与该领域的其他科学家或从业者实际相关的问题。
子组分析背后的想法是,元分析不仅仅是计算平均效应量,它也可以是一种研究我们证据中变异的工具。在子组分析中,我们不仅仅将异质性视为一种麻烦,而是将其视为有趣的变异,这种变异可能可以用科学假设来解释,也可能无法解释。在最好的情况下,这可以进一步加深我们对周围世界的理解,或者至少产生指导未来决策的实际见解。
在本章中,我们将描述子组分析背后的统计模型,以及我们如何在 R 中直接进行分析。
固定效应(复数)模型
在子组分析中,我们假设元分析中的研究并非来自一个总体。相反,我们假设它们属于不同的子组,并且每个子组都有其自身真实的总体效应。我们的目标是拒绝子组间效应量没有差异的零假设。
子组分析的计算包括两个部分:首先,我们汇集每个子组中的效应。随后,使用统计检验比较子组的效应 [@borenstein2013meta]。
汇集子组中的效应
第一部分相当简单,因为与没有子组的元分析(参见第 @ref(fem-rem) 章)的标准相同。如果我们假设子组中的所有研究都来自同一总体,并且具有一个共享的真实效应,我们可以使用固定效应模型。正如我们之前提到的,即使我们将研究划分为更小的组,这种假设在实践中也很难成立。
因此,另一种选择是使用随机效应模型。这假设子组内的研究来自一个总体集合,我们想要估计这些总体的平均值。与正常元分析的区别在于,我们进行几个独立的随机效应元分析,每个子组一个。从逻辑上讲,这会导致每个子组 \(g\) 的汇集效应 \(\hat\mu_g\)。
由于每个子组都有其自身独立的元分析,因此 \(\tau^2\) 异质性的估计也会因组而异。然而,在实践中,各个异质性值 \(\hat\tau^2_g\) 通常会被替换为跨子组汇集的 \(\tau^2\) 版本。
这意味着假设所有子组共享研究间异质性的共同估计。这主要是出于实际原因。当子组中的研究数量很少时,例如 \(k_g \leq 5\) [@borenstein2011introduction, chapter 19],\(\tau^2\) 的估计值可能不精确。在这种情况下,最好计算一个跨所有子组使用的 \(\tau^2\) 的汇集版本,而不是依赖于一个子组中研究间异质性的非常不精确的估计。
比较子组效应
下一步,我们评估 \(G\) 个子组之间是否存在真实差异。假设是子组是不同的,这意味着至少有一个子组是不同研究总体的一部分。
测试这一点的一个优雅方法是假装子组的汇集效应实际上只不过是一项大型研究的观察到的效应量[参见 @borenstein2011introduction, chapter 19]。例如,如果我们进行一个 \(G=3\) 个子组的子组分析,我们假装我们已经计算了三项大型研究的观察到的效应量(和标准误差)。
一旦我们这样看待子组,就很明显,我们问自己的问题与我们在评估正常元分析的异质性时面临的问题非常相似。我们想知道效应量的差异仅仅是由于抽样误差造成的,还是由于效应量的真实差异造成的。
因此,我们使用 \(Q\) 的值来确定子组差异是否足够大,以至于不能仅用抽样误差来解释。假设子组效应是观察到的效应量,我们计算 \(Q\) 的值。假设一个自由度为 \(G-1\) 的 \(\chi^2\) 分布,\(Q\) 的这个观察到的值与它的预期值进行比较(第 @ref(cochran-q) 章)。
当 \(Q\) 的观察值明显大于预期值时,\(Q\) 检验的 \(p\) 值将变得显著。这表明子组之间的真实效应量存在差异。这个 \(Q\) 检验是一个总括检验。它检验所有子组效应量相等的零假设,并且当至少两个子组或其组合存在差异时,该检验是显著的。
虽然我们通常假设子组内的研究符合随机效应模型,但在汇集的子组水平上,情况看起来有所不同。Borenstein 和 Higgins [-@borenstein2013meta] 认为,在许多领域中,我们选择分析的子组不能被看作是从可能的子组“集合”中随机抽取的,而是代表我们想要检查的特征的固定水平。以就业状况为例。这个特征有两个固定的子组,“已就业”和“未就业”。例如,对于患有和不患有特定合并症的患者的研究,情况也是如此。
Borenstein 和 Higgins 将子组分析的模型称为固定效应(复数)模型。之所以添加“复数”一词,是因为我们必须将其与标准的固定效应模型区分开来。固定效应(复数)模型可以看作是一种混合生物,既包含固定效应模型的特征,又包含随机效应模型的特征。与随机效应模型一样,我们假设存在不止一个真实效应量,因为我们的数据中存在子组。
然而,我们不将子组视为从整个子组集合中随机抽取的。我们的子组水平是固定的,并且是详尽的,这意味着不需要推广。这清楚地表明了为什么我们将生成子组数据的过程称为固定效应“复数”模型:因为存在几个真实的效应量,但是真实的效应量代表假设为固定的子组水平。
Borenstein 及其同事 [-@borenstein2011introduction, chapter 19] 认为,所有这些可能让我们感到有点困惑,因为“固定”一词在统计学中可以意味着不同的东西。在传统的元分析中,“固定效应”一词与“共同效应”同义。然而,在子组分析的上下文中,我们说“固定效应”是为了强调它们“不是随机的”。它们不仅仅是我们旨在推广到的一个总括分布的随机表现,而是变量可以归入的真实和唯一类别。
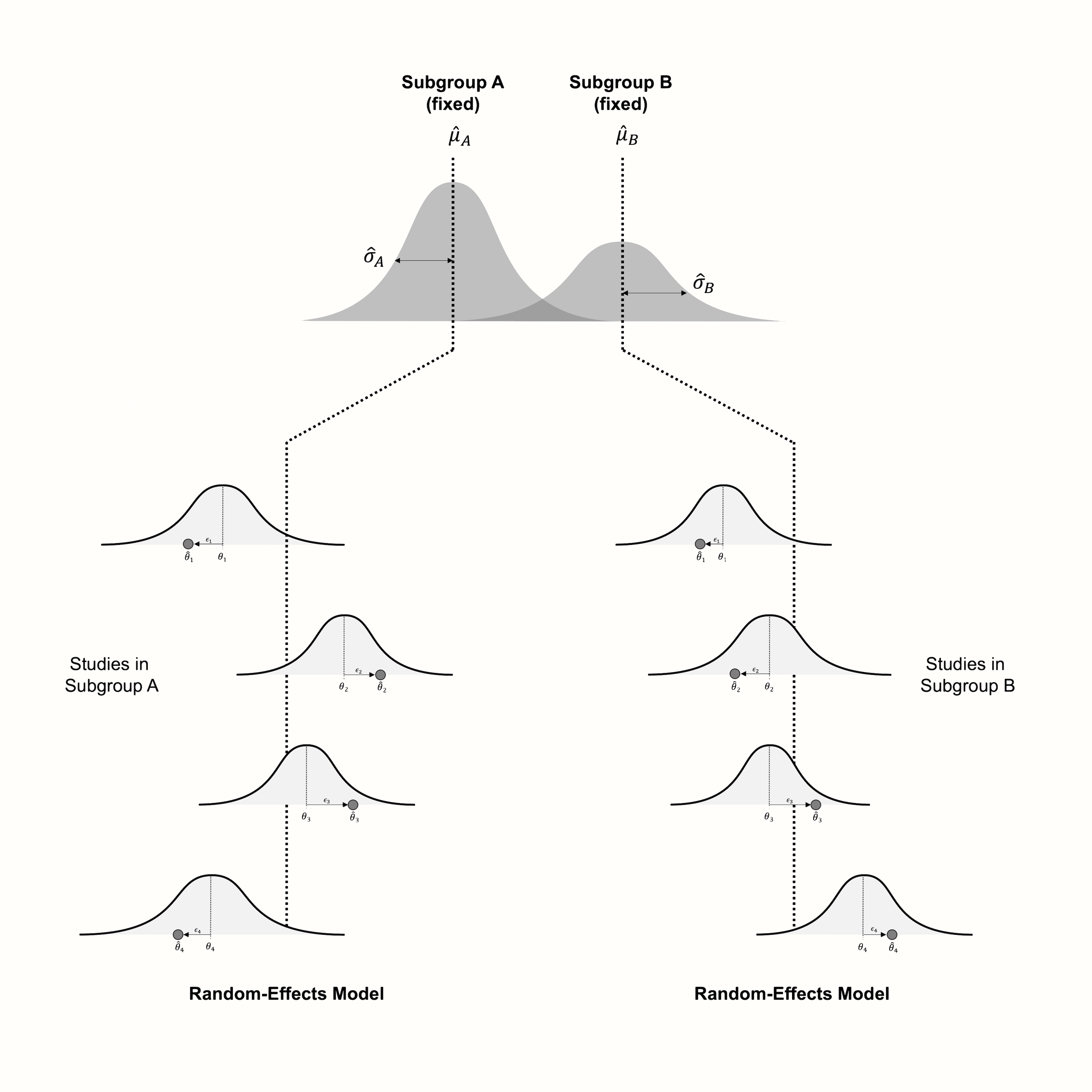
图 @ref(fig:subgroups) 可视化了固定效应(复数)模型,假设子组内的研究遵循随机效应模型。
具有固定水平的子组变量的一些示例
- 年龄组:儿童、年轻人、成人、老年人。
- 文化背景:西方、非西方。
- 对照组:替代治疗、最小治疗、不治疗。
- 用于测量结果的工具:自我报告、专家评定。
- 研究质量:高、低、不明确。
- 物种:植物、动物。
- 设置:学校、医院、私人家庭。
请注意,子组的具体选择和定义可以而且应该根据您的元分析的目的和范围进行调整。
因为固定效应(复数)模型既包含随机效应(子组内),又包含固定效应(因为假设子组是固定的),所以在文献中也称为混合效应模型。我们之前在第 @ref(pooling-props) 章中已经遇到过这个术语,我们在那里讨论了一种不同类型的(广义)混合效应模型,该模型可用于汇集,例如,比例。
我们用于子组分析的模型与其他也经常用于元分析的方法密切相关。在第 @ref(metareg) 章中,我们将展示子组分析只是元回归的一个特例,为此我们也使用混合效应模型。
此外,子组水平也可能不能假设为固定的。想象一下,我们想要评估效应量是否因观察到效应的位置而异。一些研究评估了在以色列的效应,一些在意大利,另一些在墨西哥,还有一些在中国大陆。有人可能会说“原籍国”不是一个具有固定水平的因素:世界上有许多国家,而我们的研究仅仅包括一个“随机”选择。
在这种情况下,不将子组建模为固定的是有意义的,而是让我们的模型估计国家之间的变异性作为随机效应。这导致了多层模型,我们将在第 @ref(multilevel-ma) 章中介绍。
子组分析的局限性和陷阱
直观地说,人们可能会认为子组分析是一种检测效应调节因素的绝佳工具。毕竟,元分析的目的是研究所有可用的证据。这意味着元分析中分析的个体总数通常会超过主要研究的数量级。
然而,不幸的是,这并不一定为我们提供更多的统计功效来检测子组差异。这有几个原因 [@hedges2004power]:
首先,请记住,在子组分析中,子组内的结果通常使用随机效应模型进行汇集。如果子组内存在大量的研究间异质性,这将降低汇集效应的精度(即增加标准误差)。然而,当子组效应估计非常不精确时,这意味着它们的置信区间将有很大的重叠。因此,即使这种差异确实存在,也更难找到子组之间的显著差异。
同样,统计功效通常也很低,因为我们想要在子组分析中检测到的效应远低于正常元分析中的效应。想象一下,我们想要检查评估通过自我报告与专家评定感兴趣的结果的研究之间的效应是否存在差异。即使存在差异,也很可能是很小的。通常可以找到治疗组和对照组之间的显著差异。然而,检测研究之间的效应量差异通常要困难得多,因为差异较小,并且需要更多的统计功效。
从以上几点得出一个重要的警告:缺乏证据并不意味着没有证据。如果我们没有发现子组之间的效应量差异,这并不自动意味着子组产生等效的结果。正如我们上面所说,有各种原因可以解释为什么我们的子组分析可能没有确定效应的真实差异所需的统计功效。如果是这种情况,那么说子组具有相同的效应将是一种严重的误解——我们根本不知道是否存在差异。当我们想要评估一种治疗方法是否比另一种更好时,这一点尤其具有爆炸性。包括公司在内的一些利益相关者,通常对显示治疗方法的等效性有既得利益。但是子组分析通常不是证明这一点的充分方法。
我们可以事先执行子组功效分析来检查统计功效是否是我们的子组分析中的一个问题。在这样的分析中,我们可以检查我们能够在子组分析中检测到的最小效应量差异。在“有用的工具”部分的 @ref(power-subgroup) 章中,我们介绍了如何在 R 中执行子组功效分析。但请注意,功效分析充其量只能被视为有用的诊断,而不是证明我们的分析的功效足以表明子组是等效的。Schwarzer 及其同事 [@schwarzer2015meta, chapter 4.3] 提到,作为一般经验法则,子组分析只有在您的元分析包含至少 \(K=\) 10 项研究时才有意义。
子组分析的另一个重要局限性是它们纯粹是观察性的 [@borenstein2013meta]。元分析通常只包括随机对照试验 (RCT),其中参与者被随机分配到治疗组或对照组。如果正确进行,此类 RCT 可以提供证据表明治疗导致了研究中观察到的组间差异。这是因为可能影响评估结果的所有相关变量在两组中都是相等的。唯一的区别是一组接受了治疗,而另一组没有。
子组分析,即使仅由随机研究组成,也不能显示因果关系。想象一下,我们的子组分析发现一种类型的治疗方法比另一种更有效。有很多原因可以解释为什么这一发现可能是虚假的;例如,可能调查治疗 A 的研究使用了与检查治疗 B 的研究不同的对照组。这意味着两种治疗方法可能同样有效——我们只是看到差异,因为治疗类型与方法学因素混淆了。这个例子应该强调,应该始终批判性地评估子组分析的结果。
最后一个重要的陷阱涉及子组的定义方式。通常,根据汇总信息将研究分类到子组中可能很诱人。Schwarzer 及其同事 [@schwarzer2015meta, chapter 4.3] 将研究的平均年龄作为一个常见的例子。假设您想评估老年人(65 岁以上)和一般成年人群之间的效应是否存在差异。因此,您根据报告的平均年龄是否高于或低于 65 岁,将研究分为这两类。
如果我们发现较高平均年龄的子组中的效应较高,我们可能会直观地认为这表明老年人的效应较高。但这种推理存在严重缺陷。当一项主要研究的平均年龄高于 65 岁时,它仍然可能包括很大一部分小于该年龄的个体。反之亦然,即使平均年龄较低,一项研究也完全有可能包括很大一部分大于 65 岁的个体。
这意味着在“老年人”子组中发现的较高效应可能仅仅是由实际年龄小于 65 岁的个体驱动的。相反,在“年轻人”子组中,较低的效应可能是由研究中年龄大于 65 岁的个体引起的。
这导致了一种自相矛盾的情况:在汇总水平上,我们发现平均年龄较高的研究具有较高的效应。但在个体水平上,情况恰恰相反:随着年龄的增长,一个人会经历较低的效应。
我们刚刚描述的场景是由所谓的生态偏差引起的 [@thompson2002should; @piantadosi1988ecological]。每当我们想要使用汇总(宏观)水平的关系来预测个体(微观)水平的关联时,就会出现这种情况。
避免生态偏差的最佳方法是永远不要在子组分析和元回归中使用汇总信息。但是,如果我们知道一项研究中的所有个体都属于一个类别,则情况会有所不同。例如,如果我们有一些研究仅包括 18 岁以下的青少年,而另一些研究仅允许成年人(18 岁以上)参与,则生态偏差的风险在很大程度上被消除。但是,仍然有可能效应差异是由混淆变量引起的,而不是由参与者的年龄引起的。
子组分析:总结了 Dos & Don’ts
- 子组分析取决于统计功效,因此当研究数量较少时(即 (K) < 10),进行子组分析通常没有意义。
- 如果您没有发现子组之间的效应量差异,这并不自动意味着子组产生等效的结果。
- 子组分析纯粹是观察性的,因此我们应该始终牢记,效应差异也可能是由混淆变量引起的。
- 在子组分析中使用汇总研究信息不是一个好主意,因为这可能会引入生态偏差。
R 中的子组分析
现在是时候在 R 中实施我们所学的内容了。使用 {meta} 包进行子组分析相对简单。在 {meta} 中的每个元分析函数中,都可以指定 subgroup 参数1。这会告诉函数哪个效应量属于哪个子组并运行子组分析。subgroup 参数接受 character、factor、logical 或 numeric 变量。我们唯一需要注意的是,同一子组中的研究具有完全相同的标签。
在这个例子中,我们再次使用我们的 m.gen 元分析对象。我们用于计算元分析的 ThirdWave 数据集包含一些带有子组信息的列。在这里,我们想要检查具有高风险与低风险偏倚的研究之间的效应量是否存在差异。偏倚风险信息存储在 RiskOfBias 列中。
让我们首先看一下这一列。在我们的代码中,我们使用 head 函数,以便只显示数据集的前几行。
library(meta)Loading required package: metadatLoading 'meta' package (version 8.1-0).
Type 'help(meta)' for a brief overview.library(dmetar)Extensive documentation for the dmetar package can be found at:
www.bookdown.org/MathiasHarrer/Doing_Meta_Analysis_in_R/data(ThirdWave)
# Show first entries of study name and 'RiskOfBias' column
head(ThirdWave[,c("Author", "RiskOfBias")]) Author RiskOfBias
1 Call et al. high
2 Cavanagh et al. low
3 DanitzOrsillo high
4 de Vibe et al. low
5 Frazier et al. low
6 Frogeli et al. lowm.gen <- metagen(TE = TE,
seTE = seTE,
studlab = Author,
data = ThirdWave,
sm = "SMD",
comb.fixed = FALSE,
comb.random = TRUE,
method.tau = "REML",
method.random.ci = "HK",
title = "Third Wave Psychotherapies")Warning: Use argument 'common' instead of 'comb.fixed' (deprecated).Warning: Use argument 'random' instead of 'comb.random' (deprecated).我们看到我们数据集中的每项研究都有一个指定其偏倚风险评估的标签。当我们使用 metagen 计算元分析时,此信息在内部保存在 m.gen 对象中。要进行子组分析,我们可以使用 update 函数,为其提供 m.gen 对象,并使用 subgroup 参数来指定我们的数据集中哪一列包含子组标签。
之前,我们还介绍了子组分析可以在子组间使用或不使用 \(\tau^2\) 的共同估计来进行。这可以通过在 {meta} 中将 tau.common 设置为 TRUE 或 FALSE 来控制。现在,让我们在每个子组中使用研究间异质性方差的单独估计。
在我们的例子中,我们想要应用固定效应(复数)模型并假设子组内的研究使用随机效应模型进行汇集。鉴于 m.gen 包含随机效应模型的结果(因为我们将 comb.fixed 设置为 FALSE 并且将 comb.random 设置为 TRUE),我们不需要更改任何内容。因为原始元分析是使用随机效应模型执行的,所以 update 自动假设子组内的研究也应该使用随机效应模型进行汇集。
因此,生成的代码如下所示:
update(m.gen,
subgroup = RiskOfBias,
tau.common = FALSE)## Review: Third Wave Psychotherapies
##
## Number of studies combined: k = 18
##
## SMD 95%-CI t p-value
## Random effects model (HK) 0.5771 [ 0.3782; 0.7760] 6.12 < 0.0001
## Prediction interval [-0.0572; 1.2115]
##
## Quantifying heterogeneity:
## tau^2 = 0.0820 [0.0295; 0.3533]; tau = 0.2863 [0.1717; 0.5944]
## I^2 = 62.6% [37.9%; 77.5%]; H = 1.64 [1.27; 2.11]
##
## Test of heterogeneity:
## Q d.f. p-value
## 45.50 17 0.0002
##
## Results for subgroups (random effects model (HK)):
## k SMD 95%-CI tau^2 tau Q I^2
## RiskOfBias = high 7 0.8126 [0.2835; 1.3417] 0.2423 0.4922 25.89 76.8%
## RiskOfBias = low 11 0.4300 [0.2770; 0.5830] 0.0099 0.0997 13.42 25.5%
##
## Test for subgroup differences (random effects model (HK)):
## Q d.f. p-value
## Between groups 2.84 1 0.0917
##
## Details on meta-analytical method:
## - Inverse variance method
## - Restricted maximum-likelihood estimator for tau^2
## - Q-Profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp (HK) adjustment for random effects model (df = 17)
## - Prediction interval based on t-distribution (df = 16)在输出中,我们看到一个名为 Results for subgroups 的新部分。输出的这一部分显示了每个子组的单独汇集效应量。我们看到有 \(k=\) 7 项研究具有高偏倚风险,有 11 项研究具有低偏倚风险。估计的研究间异质性差异很大,高偏倚风险研究中的 \(I^2=\) 77%,而低风险研究中的 \(I^2\) 只有 26%。
子组的效应量也不同。对于 \(g=\) 0.43,低偏倚风险研究中的效应估计小于高偏倚风险研究中的效应估计。这是一个常见的发现,因为有偏倚的研究更有可能高估治疗的效果。
但是这种差异在统计上是否显著?我们可以通过查看 Test for subgroup differences 的结果来检查这一点。这向我们展示了 \(Q\) 检验,在我们的示例中,它基于 2 个子组,基于一个自由度。检验的 \(p\) 值为 0.09,大于传统的显著性阈值,但仍然表明趋势水平上的差异。
如果我们假设两个子组中 \(\tau^2\) 的共同估计,我们也可以检查结果。我们只需要将 tau.common 设置为 TRUE。
update(m.gen, subgroup = RiskOfBias, tau.common = TRUE)## [...]
## k SMD 95%-CI tau^2 tau Q I^2
## RiskOfBias = high 7 0.7691 [0.2533; 1.2848] 0.0691 0.2630 25.89 76.8%
## RiskOfBias = low 11 0.4698 [0.3015; 0.6382] 0.0691 0.2630 13.42 25.5%
##
## Test for subgroup differences (random effects model (HK)):
## Q d.f. p-value
## Between groups 1.79 1 0.1814
## Within groups 39.31 16 0.0010
##
## Details on meta-analytical method:
## - Inverse variance method
## - Restricted maximum-likelihood estimator for tau^2
## (assuming common tau^2 in subgroups)
## [...]在输出中,我们看到估计的研究间异质性方差为 \(\tau^2=\) 0.069,并且在两个子组中相同。我们得到了两个 \(Q\) 检验:一个组间(实际的子组检验),另一个是子组内异质性。
与正常的元分析一样,后者只是表明子组中存在过多的变异性(\(p=\) 0.001)。子组差异检验再次表明,低偏倚风险和高偏倚风险研究之间没有显著差异(\(p=\) 0.181)。
我们现在假设 \(\tau^2\) 的独立或共同估计来探索结果。由于我们不知道有什么好的理由假设两个子组中的异质性是相等的,并且考虑到我们在每个子组中至少有 \(k=\) 7 项研究,因此可能适合使用 \(\tau^2\) 的单独估计。然而,我们看到,无论如何,至少在我们的示例中,我们对结果的解释对于这两种方法都是相似的。
报告子组分析的结果
子组分析的结果通常以表格形式报告,表格显示了每个子组中的估计效应和异质性,以及子组差异检验的 \(p\) 值。
Warning: 'xfun::attr()' is deprecated.
Use 'xfun::attr2()' instead.
See help("Deprecated")
Warning: 'xfun::attr()' is deprecated.
Use 'xfun::attr2()' instead.
See help("Deprecated")| $g$ | 95\%CI | $p$ | $I^2$ | 95\%CI | $p$ (subgroup) | |
|---|---|---|---|---|---|---|
| Risk of Bias | 0.092 | |||||
| - High | 0.81 | 0.28-1.34 | 0.009 | 0.77 | 0.51-0.89 | |
| - Low | 0.43 | 0.28-0.58 | < 0.001 | 0.25 | 0.00-0.63 |
在上表中,第三列中的两个 \(p\) 值显示了特定于子组的效应是否显著。我们可以看到,高偏倚风险和低偏倚风险研究都是这种情况。与此同时,\(p_{\textsf{subgroup}}\) 下的值显示,高偏倚风险和低偏倚风险研究之间的效应_差异_不显著。
要提取特定于子组的 \(p\) 值,需要将 update 的结果保存到对象中,然后使用 $ 运算符从该对象中提取 pval.random.w 元素。
\[\tag*{$\blacksquare$}\]
问题与解答
测试您的知识!
- 在最好的情况下,子组分析可以告诉我们什么影响和离群值分析无法告诉我们的信息?
- 为什么子组分析背后的模型被称为固定效应(复数)模型?
- 作为您的元分析的一部分,您想检查教育培训计划的效果是否因其交付的学区而异。使用固定效应(复数)模型进行子组分析是否适合回答这个问题?
- 您的一个朋友进行了一项元分析,其中包含总共 9 项研究。其中五项研究属于一个子组,四项研究属于另一个子组。她问您进行子组分析是否有意义。您会推荐什么?
- 您找到了一项元分析,其中作者声称分析的治疗方法在女性中比男性更有效。这一发现是基于一项子组分析,其中研究根据研究人群中包含的女性比例分为几组。这一发现是否可信,为什么(不)?
总结
尽管有很多方法可以评估元分析的异质性,但这些方法并没有告诉我们为什么我们在数据中发现了过多的变异性。子组分析允许我们检验关于为什么一些研究的真实效应量高于或低于其他研究的假设。
对于子组分析,我们通常假设一个固定效应(复数)模型。在大多数情况下,子组内的研究使用随机效应模型进行汇集。随后,使用基于总体子组结果的 \(Q\) 检验来确定组之间是否存在显著差异。
子组分析模型被称为“固定效应”模型,因为假设不同的类别本身是固定的。子组水平不被视为从可能的类别集合中随机抽取的。它们代表子组变量可以采用的唯一值。
在计算子组分析时,我们必须决定是应该使用单独的还是共同的研究间异质性估计来汇集子组内的结果。
子组分析并非万能药。它们通常缺乏检测子组差异所需的统计功效。因此,子组差异的非显著性检验并不自动意味着子组产生等效的结果。
Footnotes
在 {meta} 的旧版本(5.0-0 之前的版本)中,此参数称为
byvar。↩︎