Mplus model85 模型讲解
来自图书《MPlus中介调节模型》
复杂中介调节模型 Mplus 实现教程
- 理论模型:
- 详细阐述研究的理论框架,明确自变量、因变量、中介变量和调节变量之间的关系。
- 说明各个变量的理论意义和它们之间的预期作用方向。
- 数学模型:
- 将理论模型转化为具体的数学方程,清楚定义路径系数。
- 例如:用回归方程描述各路径之间的关系。
- 数学推导:
- 展示如何基于数学模型推导出直接效应、间接效应和调节效应的公式。
- 说明如何计算总效应,以及如何检验各项效应的显著性。
- 代码解读:
- 逐步解释 Mplus 代码的每一部分,包括变量定义、模型设定、参数估计和结果输出。
- 提供代码运行结果的解释,并指导如何解读输出结果。
理论模型
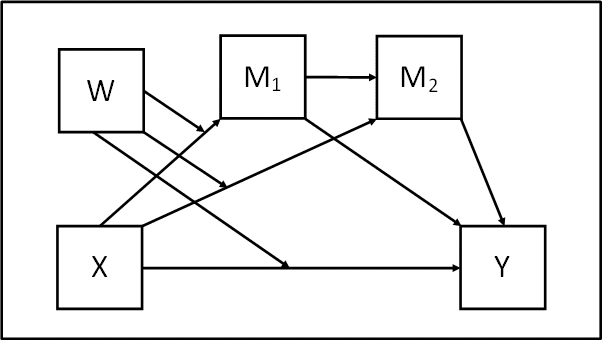
数学模型
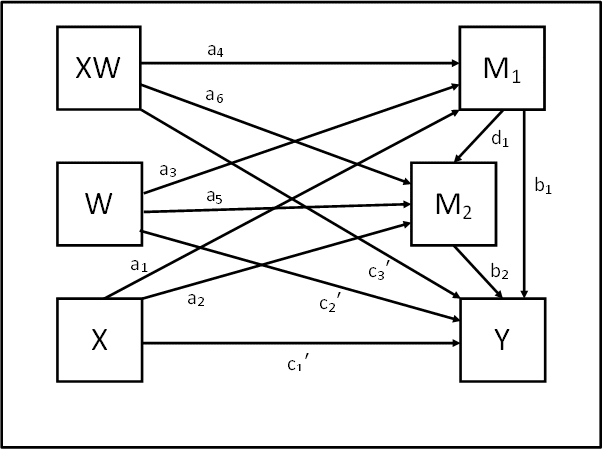
数学公式1
数学公式2
模型方程:
Y = b0 + b1M1 + b2M2 + c1'X + c2'W + c3'XW
M1 = a01 + a1X + a3W + a4XW
M2 = a02 + a2X + a5W + a6XW + d1M1
代入和展开:
Y = b0 + b1(a01 + a1X + a3W + a4XW) + b2(a02 + a2X + a5W + a6XW + d1(a01 + a1X + a3W + a4XW)) + c1'X + c2'W + c3'XW
Y = b0 + a01b1 + a1b1X + a3b1W + a4b1XW + a02b2 + a2b2X + a5b2W + a6b2XW + a01d1b2 + a1d1b2X + a3d1b2W + a4d1b2XW + c1'X + c2'W + c3'XW数学公式3
模型方程:
Y = b0 + b1M1 + b2M2 + c1'X + c2'W + c3'XW
M1 = a01 + a1X + a3W + a4XW
M2 = a02 + a2X + a5W + a6XW + d1M1
代入和展开:
Y = b0 + b1(a01 + a1X + a3W + a4XW) + b2(a02 + a2X + a5W + a6XW + d1(a01 + a1X + a3W + a4XW)) + c1'X + c2'W + c3'XW
Y = b0 + a01b1 + a1b1X + a3b1W + a4b1XW + a02b2 + a2b2X + a5b2W + a6b2XW + a01d1b2 + a1d1b2X + a3d1b2W + a4d1b2XW + c1'X + c2'W + c3'XW
合并同类项:
Y = (b0 + a01b1 + a3b1W + a02b2 + a5b2W + a01d1b2 + a3d1b2W + c2'W) + (a1b1 + a4b1W + a2b2 + a6b2W + a1d1b2 + a4d1b2W + c1' + c3'W)X数学公式4
模型方程:
Y = b0 + b1M1 + b2M2 + c1'X + c2'W + c3'XW
M1 = a01 + a1X + a3W + a4XW
M2 = a02 + a2X + a5W + a6XW + d1M1
代入和展开:
Y = b0 + b1(a01 + a1X + a3W + a4XW) + b2(a02 + a2X + a5W + a6XW + d1(a01 + a1X + a3W + a4XW)) + c1'X + c2'W + c3'XW
Y = b0 + a01b1 + a1b1X + a3b1W + a4b1XW + a02b2 + a2b2X + a5b2W + a6b2XW + a01d1b2 + a1d1b2X + a3d1b2W + a4d1b2XW + c1'X + c2'W + c3'XW
合并同类项:
Y = (b0 + a01b1 + a3b1W + a02b2 + a5b2W + a01d1b2 + a3d1b2W + c2'W) + (a1b1 + a4b1W + a2b2 + a6b2W + a1d1b2 + a4d1b2W + c1' + c3'W)X
结果:
X对Y的三个有条件间接效应 (Conditional indirect effects):
通过 M1: (a1 + a4W)b1
通过 M2: (a2 + a6W)b2
通过 M1 和 M2: (a1 + a4W)d1b2
X对Y的一个有条件直接效应 (Conditional direct effect):
c1' + c3'W代码解读1
代码解读2
代码解读3
代码解读4
USEVARIABLES = X M1 M2 W Y XW;
! Create interaction term
DEFINE:
XW = X*W;
ANALYSIS:
TYPE = GENERAL;
ESTIMATOR = ML;
BOOTSTRAP = 10000;
MODEL:
Y ON M1 (b1);
Y ON M2 (b2);
Y ON X (cdash1);
Y ON W (cdash2);
Y ON XW (cdash3);
M1 ON X (a1);
M1 ON W (a3);
M1 ON XW (a4);
M2 ON X (a2);
M2 ON W (a5);
M2 ON XW (a6);
M2 ON M1 (d1);代码解读5
USEVARIABLES = X M1 M2 W Y XW;
! Create interaction term
DEFINE:
XW = X*W;
ANALYSIS:
TYPE = GENERAL;
ESTIMATOR = ML;
BOOTSTRAP = 10000;
MODEL:
Y ON M1 (b1);
Y ON M2 (b2);
Y ON X (cdash1);
Y ON W (cdash2);
Y ON XW (cdash3);
M1 ON X (a1);
M1 ON W (a3);
M1 ON XW (a4);
M2 ON X (a2);
M2 ON W (a5);
M2 ON XW (a6);
M2 ON M1 (d1);
MODEL CONSTRAINT:
NEW(LOW_W MED_W HIGH_W
LWa1b1 MWa1b1 HWa1b1
LWa2b2 MWa2b2 HWa2b2
LWa1d1b2 MWa1d1b2 HWa1d1b2
IMM_A IMM_B IMM_C
DIR_LW DIR_MW DIR_HW
TOT_LOWW TOT_MEDW TOT_HIW);
LOW_W = #LOWW;
! replace #LOWW in the code with your chosen low value of W
MED_W = #MEDW;
! replace #MEDW in the code with your chosen medium value of W
HIGH_W = #HIGHW;
! replace #HIGHW in the code with your chosen high value of W
! Now calc indirect, direct and total effects for each value of W
! Conditional indirect effects of X on Y via M1 only given values of W
LWa1b1 = a1*b1 + a4*b1*LOW_W;
MWa1b1 = a1*b1 + a4*b1*MED_W;
HWa1b1 = a1*b1 + a4*b1*HIGH_W;
! Conditional indirect effects of X on Y via M2 only given values of W
LWa2b2 = a2*b2 + a6*b2*LOW_W;
MWa2b2 = a2*b2 + a6*b2*MED_W;
HWa2b2 = a2*b2 + a6*b2*HIGH_W;
! Conditional indirect effects of X on Y via M1 and M2 given values of W
LWa1d1b2 = a1*d1*b2 + a4*d1*b2*LOW_W;
MWa1d1b2 = a1*d1*b2 + a4*d1*b2*MED_W;
HWa1d1b2 = a1*d1*b2 + a4*d1*b2*HIGH_W;
! Indices of Moderated Mediation
IMM_A = a4*b1;
IMM_B = a4*d1*b2;
IMM_C = a6*b2;
! Conditional direct effects of X on Y given values of W
DIR_LW = cdash1 + cdash3*LOW_W;
DIR_MW = cdash1 + cdash3*MED_W;
DIR_HW = cdash1 + cdash3*HIGH_W;
! Conditional total effects of X on Y given values of W
TOT_LOWW = LWa1d1b2 + LWa1b1 + LWa2b2 + DIR_LW;
TOT_MEDW = MWa1d1b2 + MWa1b1 + MWa2b2 + DIR_MW;
TOT_HIW = HWa1d1b2 + HWa1b1 + HWa2b2 + DIR_HW;代码解读6
USEVARIABLES = X M1 M2 W Y XW;
! Create interaction term
DEFINE:
XW = X*W;
ANALYSIS:
TYPE = GENERAL;
ESTIMATOR = ML;
BOOTSTRAP = 10000;
MODEL:
Y ON M1 (b1);
Y ON M2 (b2);
Y ON X (cdash1);
Y ON W (cdash2);
Y ON XW (cdash3);
M1 ON X (a1);
M1 ON W (a3);
M1 ON XW (a4);
M2 ON X (a2);
M2 ON W (a5);
M2 ON XW (a6);
M2 ON M1 (d1);
MODEL CONSTRAINT:
NEW(LOW_W MED_W HIGH_W
LWa1b1 MWa1b1 HWa1b1
LWa2b2 MWa2b2 HWa2b2
LWa1d1b2 MWa1d1b2 HWa1d1b2
IMM_A IMM_B IMM_C
DIR_LW DIR_MW DIR_HW
TOT_LOWW TOT_MEDW TOT_HIW);
LOW_W = #LOWW;
! replace #LOWW in the code with your chosen low value of W
MED_W = #MEDW;
! replace #MEDW in the code with your chosen medium value of W
HIGH_W = #HIGHW;
! replace #HIGHW in the code with your chosen high value of W
! Now calc indirect, direct and total effects for each value of W
! Conditional indirect effects of X on Y via M1 only given values of W
LWa1b1 = a1*b1 + a4*b1*LOW_W;
MWa1b1 = a1*b1 + a4*b1*MED_W;
HWa1b1 = a1*b1 + a4*b1*HIGH_W;
! Conditional indirect effects of X on Y via M2 only given values of W
LWa2b2 = a2*b2 + a6*b2*LOW_W;
MWa2b2 = a2*b2 + a6*b2*MED_W;
HWa2b2 = a2*b2 + a6*b2*HIGH_W;
! Conditional indirect effects of X on Y via M1 and M2 given values of W
LWa1d1b2 = a1*d1*b2 + a4*d1*b2*LOW_W;
MWa1d1b2 = a1*d1*b2 + a4*d1*b2*MED_W;
HWa1d1b2 = a1*d1*b2 + a4*d1*b2*HIGH_W;
! Indices of Moderated Mediation
IMM_A = a4*b1;
IMM_B = a4*d1*b2;
IMM_C = a6*b2;
! Conditional direct effects of X on Y given values of W
DIR_LW = cdash1 + cdash3*LOW_W;
DIR_MW = cdash1 + cdash3*MED_W;
DIR_HW = cdash1 + cdash3*HIGH_W;
! Conditional total effects of X on Y given values of W
TOT_LOWW = LWa1d1b2 + LWa1b1 + LWa2b2 + DIR_LW;
TOT_MEDW = MWa1d1b2 + MWa1b1 + MWa2b2 + DIR_MW;
TOT_HIW = HWa1d1b2 + HWa1b1 + HWa2b2 + DIR_HW;
! Use loop plot to plot total effect of X on Y for low, med, high values of W
! NOTE - values of 1,5 in LOOP() statement need to be replaced by
! logical min and max limits of predictor X used in analysis
PLOT(LOMOD MEDMOD HIMOD);
LOOP(XVAL,1,5,0.1);
LOMOD = TOT_LOWW*XVAL;
MEDMOD = TOT_MEDW*XVAL;
HIMOD = TOT_HIW*XVAL;代码解读7
USEVARIABLES = X M1 M2 W Y XW;
! Create interaction term
DEFINE:
XW = X*W;
ANALYSIS:
TYPE = GENERAL;
ESTIMATOR = ML;
BOOTSTRAP = 10000;
MODEL:
Y ON M1 (b1);
Y ON M2 (b2);
Y ON X (cdash1);
Y ON W (cdash2);
Y ON XW (cdash3);
M1 ON X (a1);
M1 ON W (a3);
M1 ON XW (a4);
M2 ON X (a2);
M2 ON W (a5);
M2 ON XW (a6);
M2 ON M1 (d1);
MODEL CONSTRAINT:
NEW(LOW_W MED_W HIGH_W
LWa1b1 MWa1b1 HWa1b1
LWa2b2 MWa2b2 HWa2b2
LWa1d1b2 MWa1d1b2 HWa1d1b2
IMM_A IMM_B IMM_C
DIR_LW DIR_MW DIR_HW
TOT_LOWW TOT_MEDW TOT_HIW);
LOW_W = #LOWW;
! replace #LOWW in the code with your chosen low value of W
MED_W = #MEDW;
! replace #MEDW in the code with your chosen medium value of W
HIGH_W = #HIGHW;
! replace #HIGHW in the code with your chosen high value of W
! Now calc indirect, direct and total effects for each value of W
! Conditional indirect effects of X on Y via M1 only given values of W
LWa1b1 = a1*b1 + a4*b1*LOW_W;
MWa1b1 = a1*b1 + a4*b1*MED_W;
HWa1b1 = a1*b1 + a4*b1*HIGH_W;
! Conditional indirect effects of X on Y via M2 only given values of W
LWa2b2 = a2*b2 + a6*b2*LOW_W;
MWa2b2 = a2*b2 + a6*b2*MED_W;
HWa2b2 = a2*b2 + a6*b2*HIGH_W;
! Conditional indirect effects of X on Y via M1 and M2 given values of W
LWa1d1b2 = a1*d1*b2 + a4*d1*b2*LOW_W;
MWa1d1b2 = a1*d1*b2 + a4*d1*b2*MED_W;
HWa1d1b2 = a1*d1*b2 + a4*d1*b2*HIGH_W;
! Indices of Moderated Mediation
IMM_A = a4*b1;
IMM_B = a4*d1*b2;
IMM_C = a6*b2;
! Conditional direct effects of X on Y given values of W
DIR_LW = cdash1 + cdash3*LOW_W;
DIR_MW = cdash1 + cdash3*MED_W;
DIR_HW = cdash1 + cdash3*HIGH_W;
! Conditional total effects of X on Y given values of W
TOT_LOWW = LWa1d1b2 + LWa1b1 + LWa2b2 + DIR_LW;
TOT_MEDW = MWa1d1b2 + MWa1b1 + MWa2b2 + DIR_MW;
TOT_HIW = HWa1d1b2 + HWa1b1 + HWa2b2 + DIR_HW;
! Use loop plot to plot total effect of X on Y for low, med, high values of W
! NOTE - values of 1,5 in LOOP() statement need to be replaced by
! logical min and max limits of predictor X used in analysis
PLOT(LOMOD MEDMOD HIMOD);
LOOP(XVAL,1,5,0.1);
LOMOD = TOT_LOWW*XVAL;
MEDMOD = TOT_MEDW*XVAL;
HIMOD = TOT_HIW*XVAL;
PLOT:
TYPE = plot2;
OUTPUT:
STAND CINT(bcbootstrap);