Mplus model81 模型讲解
来自图书《MPlus中介调节模型》
Mplus 多重中介模型分析教程
- 理论模型
- 数学模型
- 数学推导
- 代码解读
理论模型
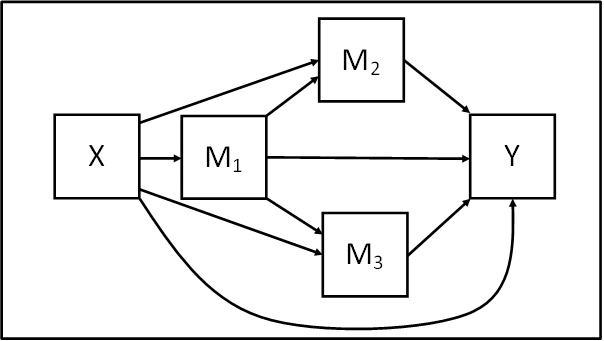
数学模型
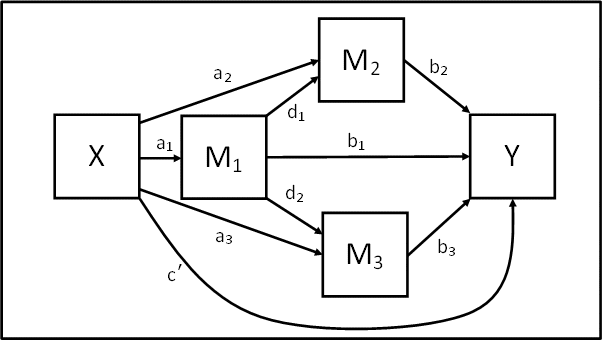
数学公式1
数学公式2
数学公式3
模型方程:
Y = b0 + b1M1 + b2M2 + b3M3 + c'X
M1 = a01 + a1X
M2 = a02 + a2X + d1M1
M3 = a03 + a3X + d2M1
将 M1 的表达式代入 Y, M2, M3 的方程中:
Y = b0 + b1(a01 + a1X) + b2M2 + b3M3 + c'X
M2 = a02 + a2X + d1(a01 + a1X)
M3 = a03 + a3X + d2(a01 + a1X)
将 M3 的表达式代入 Y 的方程中:
Y = b0 + b1(a01 + a1X) + b2(a02 + a2X + d1(a01 + a1X)) + b3(a03 + a3X + d2(a01 + a1X)) + c'X数学公式4
模型方程:
Y = b0 + b1M1 + b2M2 + b3M3 + c'X
M1 = a01 + a1X
M2 = a02 + a2X + d1M1
M3 = a03 + a3X + d2M1
将 M1 的表达式代入 Y, M2, M3 的方程中:
Y = b0 + b1(a01 + a1X) + b2M2 + b3M3 + c'X
M2 = a02 + a2X + d1(a01 + a1X)
M3 = a03 + a3X + d2(a01 + a1X)
将 M3 的表达式代入 Y 的方程中:
Y = b0 + b1(a01 + a1X) + b2(a02 + a2X + d1(a01 + a1X)) + b3(a03 + a3X + d2(a01 + a1X)) + c'X
展开括号:
Y = b0 + a01b1 + a1b1X + a02b2 + a2b2X + a01b2d1 + a1b2d1X + a03b3 + a3b3X + a01b3d2 + a1b3d2X + c'X数学公式5
模型方程:
Y = b0 + b1M1 + b2M2 + b3M3 + c'X
M1 = a01 + a1X
M2 = a02 + a2X + d1M1
M3 = a03 + a3X + d2M1
将 M1 的表达式代入 Y, M2, M3 的方程中:
Y = b0 + b1(a01 + a1X) + b2M2 + b3M3 + c'X
M2 = a02 + a2X + d1(a01 + a1X)
M3 = a03 + a3X + d2(a01 + a1X)
将 M3 的表达式代入 Y 的方程中:
Y = b0 + b1(a01 + a1X) + b2(a02 + a2X + d1(a01 + a1X)) + b3(a03 + a3X + d2(a01 + a1X)) + c'X
展开括号:
Y = b0 + a01b1 + a1b1X + a02b2 + a2b2X + a01b2d1 + a1b2d1X + a03b3 + a3b3X + a01b3d2 + a1b3d2X + c'X
合并同类项,整理成 Y = a + bX 的形式:
Y = (b0 + a01b1 + a02b2 + a01b2d1 + a03b3 + a01b3d2) + (a1b1 + a2b2 + a3b3 + a1b2d1 + a1b3d2 + c')X数学公式6
模型方程:
Y = b0 + b1M1 + b2M2 + b3M3 + c'X
M1 = a01 + a1X
M2 = a02 + a2X + d1M1
M3 = a03 + a3X + d2M1
将 M1 的表达式代入 Y, M2, M3 的方程中:
Y = b0 + b1(a01 + a1X) + b2M2 + b3M3 + c'X
M2 = a02 + a2X + d1(a01 + a1X)
M3 = a03 + a3X + d2(a01 + a1X)
将 M3 的表达式代入 Y 的方程中:
Y = b0 + b1(a01 + a1X) + b2(a02 + a2X + d1(a01 + a1X)) + b3(a03 + a3X + d2(a01 + a1X)) + c'X
展开括号:
Y = b0 + a01b1 + a1b1X + a02b2 + a2b2X + a01b2d1 + a1b2d1X + a03b3 + a3b3X + a01b3d2 + a1b3d2X + c'X
合并同类项,整理成 Y = a + bX 的形式:
Y = (b0 + a01b1 + a02b2 + a01b2d1 + a03b3 + a01b3d2) + (a1b1 + a2b2 + a3b3 + a1b2d1 + a1b3d2 + c')X
最终结果:
截距项(常数项)为:b0 + a01b1 + a02b2 + a01b2d1 + a03b3 + a01b3d2
X 的总效应(系数)为:a1b1 + a2b2 + a3b3 + a1b2d1 + a1b3d2 + c'数学公式7
模型方程:
Y = b0 + b1M1 + b2M2 + b3M3 + c'X
M1 = a01 + a1X
M2 = a02 + a2X + d1M1
M3 = a03 + a3X + d2M1
将 M1 的表达式代入 Y, M2, M3 的方程中:
Y = b0 + b1(a01 + a1X) + b2M2 + b3M3 + c'X
M2 = a02 + a2X + d1(a01 + a1X)
M3 = a03 + a3X + d2(a01 + a1X)
将 M3 的表达式代入 Y 的方程中:
Y = b0 + b1(a01 + a1X) + b2(a02 + a2X + d1(a01 + a1X)) + b3(a03 + a3X + d2(a01 + a1X)) + c'X
展开括号:
Y = b0 + a01b1 + a1b1X + a02b2 + a2b2X + a01b2d1 + a1b2d1X + a03b3 + a3b3X + a01b3d2 + a1b3d2X + c'X
合并同类项,整理成 Y = a + bX 的形式:
Y = (b0 + a01b1 + a02b2 + a01b2d1 + a03b3 + a01b3d2) + (a1b1 + a2b2 + a3b3 + a1b2d1 + a1b3d2 + c')X
最终结果:
截距项(常数项)为:b0 + a01b1 + a02b2 + a01b2d1 + a03b3 + a01b3d2
X 的总效应(系数)为:a1b1 + a2b2 + a3b3 + a1b2d1 + a1b3d2 + c'
间接效应和直接效应:
X 对 Y 的五种间接效应分别是:a1b1, a2b2, a3b3, a1d1b2, a1d2b3
X 对 Y 的直接效应为:c'代码解读1
代码解读2
代码解读3
! Predictor variable - X
! Mediator variable(s) – M1, M2, M3
! Moderator variable(s) - none
! Outcome variable - Y
USEVARIABLES = X M1 M2 M3 Y;
ANALYSIS:
TYPE = GENERAL;
ESTIMATOR = ML;
BOOTSTRAP = 10000;
! In model statement name each path using parentheses
MODEL:
Y ON M1 (b1);
Y ON M2 (b2);
Y ON M3 (b3);
Y ON X (cdash);
! direct effect of X on Y
M1 ON X (a1);
M2 ON X (a2);
M3 ON X (a3);
M2 ON M1 (d1);
M3 ON M1 (d2);代码解读4
! Predictor variable - X
! Mediator variable(s) – M1, M2, M3
! Moderator variable(s) - none
! Outcome variable - Y
USEVARIABLES = X M1 M2 M3 Y;
ANALYSIS:
TYPE = GENERAL;
ESTIMATOR = ML;
BOOTSTRAP = 10000;
! In model statement name each path using parentheses
MODEL:
Y ON M1 (b1);
Y ON M2 (b2);
Y ON M3 (b3);
Y ON X (cdash);
! direct effect of X on Y
M1 ON X (a1);
M2 ON X (a2);
M3 ON X (a3);
M2 ON M1 (d1);
M3 ON M1 (d2);
! Use model constraint to calculate specific indirect paths and total indirect effect
MODEL CONSTRAINT:
NEW(a1b1 a2b2 a3b3 a1d1b2 a1d2b3 TOTALIND TOTAL);
a1b1 = a1*b1;
! Specific indirect effect of X on Y via M1 only
a2b2 = a2*b2;
! Specific indirect effect of X on Y via M2 only
a3b3 = a3*b3;
! Specific indirect effect of X on Y via M3 only
a1d1b2 = a1*d1*b2;
! Specific indirect effect of X on Y via M1 and M2
a1d2b3 = a1*d2*b3;
! Specific indirect effect of X on Y via M1 and M3
TOTALIND = a1b1 + a2b2 + a3b3 + a1d1b2 + a1d2b3;
! Total indirect effect of X on Y via M1, M2, M3
TOTAL = a1b1 + a2b2 + a3b3 + a1d1b2 + a1d2b3 + cdash;
! Total effect of X on Y代码解读5
! Predictor variable - X
! Mediator variable(s) – M1, M2, M3
! Moderator variable(s) - none
! Outcome variable - Y
USEVARIABLES = X M1 M2 M3 Y;
ANALYSIS:
TYPE = GENERAL;
ESTIMATOR = ML;
BOOTSTRAP = 10000;
! In model statement name each path using parentheses
MODEL:
Y ON M1 (b1);
Y ON M2 (b2);
Y ON M3 (b3);
Y ON X (cdash);
! direct effect of X on Y
M1 ON X (a1);
M2 ON X (a2);
M3 ON X (a3);
M2 ON M1 (d1);
M3 ON M1 (d2);
! Use model constraint to calculate specific indirect paths and total indirect effect
MODEL CONSTRAINT:
NEW(a1b1 a2b2 a3b3 a1d1b2 a1d2b3 TOTALIND TOTAL);
a1b1 = a1*b1;
! Specific indirect effect of X on Y via M1 only
a2b2 = a2*b2;
! Specific indirect effect of X on Y via M2 only
a3b3 = a3*b3;
! Specific indirect effect of X on Y via M3 only
a1d1b2 = a1*d1*b2;
! Specific indirect effect of X on Y via M1 and M2
a1d2b3 = a1*d2*b3;
! Specific indirect effect of X on Y via M1 and M3
TOTALIND = a1b1 + a2b2 + a3b3 + a1d1b2 + a1d2b3;
! Total indirect effect of X on Y via M1, M2, M3
TOTAL = a1b1 + a2b2 + a3b3 + a1d1b2 + a1d2b3 + cdash;
! Total effect of X on Y
OUTPUT:
STAND CINT(bcbootstrap);