Mplus model72latent 模型讲解
来自图书《MPlus中介调节模型》
PPT标题:Mplus调节中介模型(潜变量)速查教程
- 理论模型
- 数学模型
- 数学推导
- 代码解读
理论模型
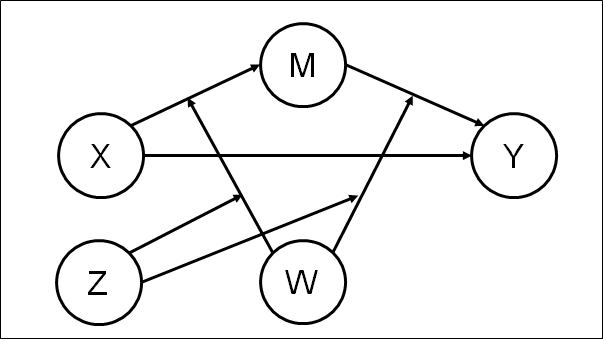
数学模型
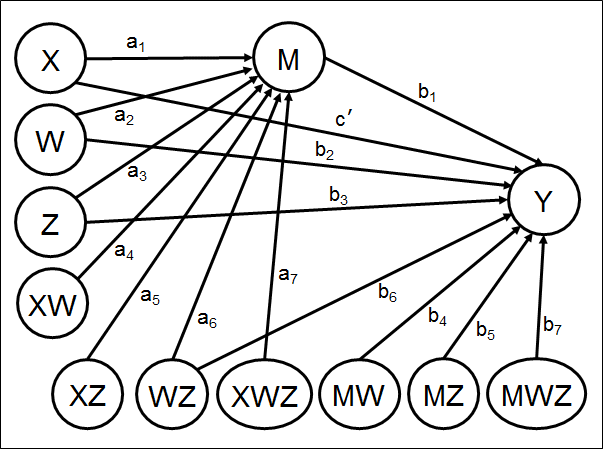
数学公式1
数学公式2
模型方程:
Y = b0 + b1M + b2W + b3Z + b4MW + b5MZ + b6WZ + b7MWZ + c'X
M = a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ
代入和展开:
Y = b0 + b1(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ) + b2W + b3Z + b4(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ)W + b5(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ)Z + b6WZ + b7(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ)WZ + c'X
Y = b0 + a0b1 + a1b1X + a2b1W + a3b1Z + a4b1XW + a5b1XZ + a6b1WZ + a7b1XWZ + b2W + b3Z + a0b4W + a1b4XW + a2b4WW + a3b4ZW + a4b4XWW + a5b4XZW + a6b4WWZ + a7b4XWWZ + a0b5Z + a1b5XZ + a2b5WZ + a3b5ZZ + a4b5XWZ + a5b5XZZ + a6b5WZZ + a7b5XWZZ + b6WZ + a0b7WZ + a1b7XWZ + a2b7WWZ + a3b7WZZ + a4b7XWWZ + a5b7XWZZ + a6b7WWZZ + a7XWWZZ + c'X数学公式3
模型方程:
Y = b0 + b1M + b2W + b3Z + b4MW + b5MZ + b6WZ + b7MWZ + c'X
M = a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ
代入和展开:
Y = b0 + b1(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ) + b2W + b3Z + b4(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ)W + b5(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ)Z + b6WZ + b7(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ)WZ + c'X
Y = b0 + a0b1 + a1b1X + a2b1W + a3b1Z + a4b1XW + a5b1XZ + a6b1WZ + a7b1XWZ + b2W + b3Z + a0b4W + a1b4XW + a2b4WW + a3b4ZW + a4b4XWW + a5b4XZW + a6b4WWZ + a7b4XWWZ + a0b5Z + a1b5XZ + a2b5WZ + a3b5ZZ + a4b5XWZ + a5b5XZZ + a6b5WZZ + a7b5XWZZ + b6WZ + a0b7WZ + a1b7XWZ + a2b7WWZ + a3b7WZZ + a4b7XWWZ + a5b7XWZZ + a6b7WWZZ + a7XWWZZ + c'X
整理和分组:
Y = (b0 + a0b1 + a2b1W + a3b1Z + a6b1WZ + b2W + b3Z + a0b4W + a2b4WW + a3b4ZW + a6b4WWZ + a0b5Z + a2b5WZ + a3b5ZZ + a6b5WZZ + b6WZ + a0b7WZ + a2b7WWZ + a3b7WZZ + a6b7WWZZ) + (a1b1 + a4b1W + a5b1Z + a7b1WZ + a1b4W + a4b4WW + a5b4ZW + a7b4WWZ + a1b5Z + a4b5WZ + a5b5ZZ + a7b5WZZ + a1b7WZ + a4b7WWZ + a5b7WZZ + a7b7WWZZ + c')X数学公式4
模型方程:
Y = b0 + b1M + b2W + b3Z + b4MW + b5MZ + b6WZ + b7MWZ + c'X
M = a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ
代入和展开:
Y = b0 + b1(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ) + b2W + b3Z + b4(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ)W + b5(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ)Z + b6WZ + b7(a0 + a1X + a2W + a3Z + a4XW + a5XZ + a6WZ + a7XWZ)WZ + c'X
Y = b0 + a0b1 + a1b1X + a2b1W + a3b1Z + a4b1XW + a5b1XZ + a6b1WZ + a7b1XWZ + b2W + b3Z + a0b4W + a1b4XW + a2b4WW + a3b4ZW + a4b4XWW + a5b4XZW + a6b4WWZ + a7b4XWWZ + a0b5Z + a1b5XZ + a2b5WZ + a3b5ZZ + a4b5XWZ + a5b5XZZ + a6b5WZZ + a7b5XWZZ + b6WZ + a0b7WZ + a1b7XWZ + a2b7WWZ + a3b7WZZ + a4b7XWWZ + a5b7XWZZ + a6b7WWZZ + a7XWWZZ + c'X
整理和分组:
Y = (b0 + a0b1 + a2b1W + a3b1Z + a6b1WZ + b2W + b3Z + a0b4W + a2b4WW + a3b4ZW + a6b4WWZ + a0b5Z + a2b5WZ + a3b5ZZ + a6b5WZZ + b6WZ + a0b7WZ + a2b7WWZ + a3b7WZZ + a6b7WWZZ) + (a1b1 + a4b1W + a5b1Z + a7b1WZ + a1b4W + a4b4WW + a5b4ZW + a7b4WWZ + a1b5Z + a4b5WZ + a5b5ZZ + a7b5WZZ + a1b7WZ + a4b7WWZ + a5b7WZZ + a7b7WWZZ + c')X
间接效应和直接效应:
间接效应 (通过M):
(a1 + a4W + a5Z + a7WZ)(b1 + b4W + b5Z + b7WZ)
直接效应 (不通过M):
c'代码解读1
代码解读2
代码解读3
USEVARIABLES = X1 X2 X3 X4 M1 M2 M3 M4
W1 W2 W3 W4 Z1 Z2 Z3 Z4
Y1 Y2 Y3 Y4;
ANALYSIS:
TYPE = GENERAL RANDOM;
ESTIMATOR = ML;
ALGORITHM = INTEGRATION;
MODEL:
! Measurement model
! Identify moderator factors by fixing variance = 1 (instead of first loading)
! This makes these factors standardised
X BY X1 X2 X3 X4;
M BY M1 M2 M3 M4;
W BY W1* W2 W3 W4;
Z BY Z1* Z2 Z3 Z4;
Y BY Y1 Y2 Y3 Y4;
W@1; Z@1;代码解读4
USEVARIABLES = X1 X2 X3 X4 M1 M2 M3 M4
W1 W2 W3 W4 Z1 Z2 Z3 Z4
Y1 Y2 Y3 Y4;
ANALYSIS:
TYPE = GENERAL RANDOM;
ESTIMATOR = ML;
ALGORITHM = INTEGRATION;
MODEL:
! Measurement model
! Identify moderator factors by fixing variance = 1 (instead of first loading)
! This makes these factors standardised
X BY X1 X2 X3 X4;
M BY M1 M2 M3 M4;
W BY W1* W2 W3 W4;
Z BY Z1* Z2 Z3 Z4;
Y BY Y1 Y2 Y3 Y4;
W@1; Z@1;
! Create latent interactions
MW | M XWITH W;
MZ | M XWITH Z;
XW | X XWITH W;
XZ | X XWITH Z;
WZ | W XWITH Z;
MWZ | M XWITH WZ;
XWZ | X XWITH WZ;代码解读5
USEVARIABLES = X1 X2 X3 X4 M1 M2 M3 M4
W1 W2 W3 W4 Z1 Z2 Z3 Z4
Y1 Y2 Y3 Y4;
ANALYSIS:
TYPE = GENERAL RANDOM;
ESTIMATOR = ML;
ALGORITHM = INTEGRATION;
MODEL:
! Measurement model
! Identify moderator factors by fixing variance = 1 (instead of first loading)
! This makes these factors standardised
X BY X1 X2 X3 X4;
M BY M1 M2 M3 M4;
W BY W1* W2 W3 W4;
Z BY Z1* Z2 Z3 Z4;
Y BY Y1 Y2 Y3 Y4;
W@1; Z@1;
! Create latent interactions
MW | M XWITH W;
MZ | M XWITH Z;
XW | X XWITH W;
XZ | X XWITH Z;
WZ | W XWITH Z;
MWZ | M XWITH WZ;
XWZ | X XWITH WZ;
! Fit structural model and name parameters
! Note that intercepts of M, Y are fixed = 0 since they are latent vars
! so no code to state and name them as parameters
Y ON M (b1);
Y ON W (b2);
Y ON Z (b3);
Y ON MW (b4);
Y ON MZ (b5);
Y ON WZ (b6);
Y ON MWZ (b7);
Y ON X(cdash);
M ON X (a1);
M ON W (a2);
M ON Z (a3);
M ON XW (a4);
M ON XZ (a5);
M ON WZ (a6);
M ON XWZ (a7);代码解读6
USEVARIABLES = X1 X2 X3 X4 M1 M2 M3 M4
W1 W2 W3 W4 Z1 Z2 Z3 Z4
Y1 Y2 Y3 Y4;
ANALYSIS:
TYPE = GENERAL RANDOM;
ESTIMATOR = ML;
ALGORITHM = INTEGRATION;
MODEL:
! Measurement model
! Identify moderator factors by fixing variance = 1 (instead of first loading)
! This makes these factors standardised
X BY X1 X2 X3 X4;
M BY M1 M2 M3 M4;
W BY W1* W2 W3 W4;
Z BY Z1* Z2 Z3 Z4;
Y BY Y1 Y2 Y3 Y4;
W@1; Z@1;
! Create latent interactions
MW | M XWITH W;
MZ | M XWITH Z;
XW | X XWITH W;
XZ | X XWITH Z;
WZ | W XWITH Z;
MWZ | M XWITH WZ;
XWZ | X XWITH WZ;
! Fit structural model and name parameters
! Note that intercepts of M, Y are fixed = 0 since they are latent vars
! so no code to state and name them as parameters
Y ON M (b1);
Y ON W (b2);
Y ON Z (b3);
Y ON MW (b4);
Y ON MZ (b5);
Y ON WZ (b6);
Y ON MWZ (b7);
Y ON X(cdash);
M ON X (a1);
M ON W (a2);
M ON Z (a3);
M ON XW (a4);
M ON XZ (a5);
M ON WZ (a6);
M ON XWZ (a7);
! Use model constraint subcommand to test conditional indirect effects
! You need to pick low, medium and high moderator values for W, Z
! for example, of 1 SD below mean, mean, 1 SD above mean
! 2 moderators, 3 values for each, gives 9 combinations
! arbitrary naming convention for conditional indirect and total effects used below:
! MEV_LOQ = medium value of V and low value of Q, etc.
MODEL CONSTRAINT:
NEW(LOW_W MED_W HIGH_W LOW_Z MED_Z HIGH_Z
ILOW_LOZ IMEW_LOZ IHIW_LOZ ILOW_MEZ IMEW_MEZ IHIW_MEZ
ILOW_HIZ IMEW_HIZ IHIW_HIZ
TLOW_LOZ TMEW_LOZ THIW_LOZ TLOW_MEZ TMEW_MEZ THIW_MEZ
TLOW_HIZ TMEW_HIZ THIW_HIZ);
LOW_W = -1;
! -1 SD below mean value of W
MED_W = 0;
! mean value of W
HIGH_W = 1;
! +1 SD above mean value of W
LOW_Z = -1;
! -1 SD below mean value of Z
MED_Z = 0;
! mean value of Z
HIGH_Z = 1;
! +1 SD above mean value of Z代码解读7
USEVARIABLES = X1 X2 X3 X4 M1 M2 M3 M4
W1 W2 W3 W4 Z1 Z2 Z3 Z4
Y1 Y2 Y3 Y4;
ANALYSIS:
TYPE = GENERAL RANDOM;
ESTIMATOR = ML;
ALGORITHM = INTEGRATION;
MODEL:
! Measurement model
! Identify moderator factors by fixing variance = 1 (instead of first loading)
! This makes these factors standardised
X BY X1 X2 X3 X4;
M BY M1 M2 M3 M4;
W BY W1* W2 W3 W4;
Z BY Z1* Z2 Z3 Z4;
Y BY Y1 Y2 Y3 Y4;
W@1; Z@1;
! Create latent interactions
MW | M XWITH W;
MZ | M XWITH Z;
XW | X XWITH W;
XZ | X XWITH Z;
WZ | W XWITH Z;
MWZ | M XWITH WZ;
XWZ | X XWITH WZ;
! Fit structural model and name parameters
! Note that intercepts of M, Y are fixed = 0 since they are latent vars
! so no code to state and name them as parameters
Y ON M (b1);
Y ON W (b2);
Y ON Z (b3);
Y ON MW (b4);
Y ON MZ (b5);
Y ON WZ (b6);
Y ON MWZ (b7);
Y ON X(cdash);
M ON X (a1);
M ON W (a2);
M ON Z (a3);
M ON XW (a4);
M ON XZ (a5);
M ON WZ (a6);
M ON XWZ (a7);
! Use model constraint subcommand to test conditional indirect effects
! You need to pick low, medium and high moderator values for W, Z
! for example, of 1 SD below mean, mean, 1 SD above mean
! 2 moderators, 3 values for each, gives 9 combinations
! arbitrary naming convention for conditional indirect and total effects used below:
! MEV_LOQ = medium value of V and low value of Q, etc.
MODEL CONSTRAINT:
NEW(LOW_W MED_W HIGH_W LOW_Z MED_Z HIGH_Z
ILOW_LOZ IMEW_LOZ IHIW_LOZ ILOW_MEZ IMEW_MEZ IHIW_MEZ
ILOW_HIZ IMEW_HIZ IHIW_HIZ
TLOW_LOZ TMEW_LOZ THIW_LOZ TLOW_MEZ TMEW_MEZ THIW_MEZ
TLOW_HIZ TMEW_HIZ THIW_HIZ);
LOW_W = -1;
! -1 SD below mean value of W
MED_W = 0;
! mean value of W
HIGH_W = 1;
! +1 SD above mean value of W
LOW_Z = -1;
! -1 SD below mean value of Z
MED_Z = 0;
! mean value of Z
HIGH_Z = 1;
! +1 SD above mean value of Z
! Calc conditional indirect effects for each combination of moderator values
ILOW_LOZ = a1*b1 + a4*b1*LOW_W + a5*b1*LOW_Z + a7*b1*LOW_W*LOW_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*LOW_Z*LOW_W +
a7*b4*LOW_W*LOW_W*LOW_Z + a1*b5*LOW_Z + a4*b5*LOW_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*LOW_W*LOW_Z*LOW_Z + a1*b7*LOW_W*LOW_Z +
a4*b7*LOW_W*LOW_W*LOW_Z + a5*b7*LOW_W*LOW_Z*LOW_Z +
a7*b7*LOW_W*LOW_W*LOW_Z*LOW_Z;
IMEW_LOZ = a1*b1 + a4*b1*MED_W + a5*b1*LOW_Z + a7*b1*MED_W*LOW_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*LOW_Z*MED_W +
a7*b4*MED_W*MED_W*LOW_Z + a1*b5*LOW_Z + a4*b5*MED_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*MED_W*LOW_Z*LOW_Z + a1*b7*MED_W*LOW_Z +
a4*b7*MED_W*MED_W*LOW_Z + a5*b7*MED_W*LOW_Z*LOW_Z +
a7*b7*MED_W*MED_W*LOW_Z*LOW_Z;
IHIW_LOZ = a1*b1 + a4*b1*HIGH_W + a5*b1*LOW_Z + a7*b1*HIGH_W*LOW_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*LOW_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*LOW_Z + a1*b5*LOW_Z + a4*b5*HIGH_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*HIGH_W*LOW_Z*LOW_Z + a1*b7*HIGH_W*LOW_Z +
a4*b7*HIGH_W*HIGH_W*LOW_Z + a5*b7*HIGH_W*LOW_Z*LOW_Z +
a7*b7*HIGH_W*HIGH_W*LOW_Z*LOW_Z;
ILOW_MEZ = a1*b1 + a4*b1*LOW_W + a5*b1*MED_Z + a7*b1*LOW_W*MED_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*MED_Z*LOW_W +
a7*b4*LOW_W*LOW_W*MED_Z + a1*b5*MED_Z + a4*b5*LOW_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*LOW_W*MED_Z*MED_Z + a1*b7*LOW_W*MED_Z +
a4*b7*LOW_W*LOW_W*MED_Z + a5*b7*LOW_W*MED_Z*MED_Z +
a7*b7*LOW_W*LOW_W*MED_Z*MED_Z;
IMEW_MEZ = a1*b1 + a4*b1*MED_W + a5*b1*MED_Z + a7*b1*MED_W*MED_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*MED_Z*MED_W +
a7*b4*MED_W*MED_W*MED_Z + a1*b5*MED_Z + a4*b5*MED_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*MED_W*MED_Z*MED_Z + a1*b7*MED_W*MED_Z +
a4*b7*MED_W*MED_W*MED_Z + a5*b7*MED_W*MED_Z*MED_Z +
a7*b7*MED_W*MED_W*MED_Z*MED_Z;
IHIW_MEZ = a1*b1 + a4*b1*HIGH_W + a5*b1*MED_Z + a7*b1*HIGH_W*MED_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*MED_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*MED_Z + a1*b5*MED_Z + a4*b5*HIGH_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*HIGH_W*MED_Z*MED_Z + a1*b7*HIGH_W*MED_Z +
a4*b7*HIGH_W*HIGH_W*MED_Z + a5*b7*HIGH_W*MED_Z*MED_Z +
a7*b7*HIGH_W*HIGH_W*MED_Z*MED_Z;
ILOW_HIZ = a1*b1 + a4*b1*LOW_W + a5*b1*HIGH_Z + a7*b1*LOW_W*HIGH_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*HIGH_Z*LOW_W +
a7*b4*LOW_W*LOW_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*LOW_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*LOW_W*HIGH_Z*HIGH_Z + a1*b7*LOW_W*HIGH_Z +
a4*b7*LOW_W*LOW_W*HIGH_Z + a5*b7*LOW_W*HIGH_Z*HIGH_Z +
a7*b7*LOW_W*LOW_W*HIGH_Z*HIGH_Z;
IMEW_HIZ = a1*b1 + a4*b1*MED_W + a5*b1*HIGH_Z + a7*b1*MED_W*HIGH_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*HIGH_Z*MED_W +
a7*b4*MED_W*MED_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*MED_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*MED_W*HIGH_Z*HIGH_Z + a1*b7*MED_W*HIGH_Z +
a4*b7*MED_W*MED_W*HIGH_Z + a5*b7*MED_W*HIGH_Z*HIGH_Z +
a7*b7*MED_W*MED_W*HIGH_Z*HIGH_Z;
IHIW_HIZ = a1*b1 + a4*b1*HIGH_W + a5*b1*HIGH_Z + a7*b1*HIGH_W*HIGH_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*HIGH_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*HIGH_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*HIGH_W*HIGH_Z*HIGH_Z + a1*b7*HIGH_W*HIGH_Z +
a4*b7*HIGH_W*HIGH_W*HIGH_Z + a5*b7*HIGH_W*HIGH_Z*HIGH_Z +
a7*b7*HIGH_W*HIGH_W*HIGH_Z*HIGH_Z;代码解读8
USEVARIABLES = X1 X2 X3 X4 M1 M2 M3 M4
W1 W2 W3 W4 Z1 Z2 Z3 Z4
Y1 Y2 Y3 Y4;
ANALYSIS:
TYPE = GENERAL RANDOM;
ESTIMATOR = ML;
ALGORITHM = INTEGRATION;
MODEL:
! Measurement model
! Identify moderator factors by fixing variance = 1 (instead of first loading)
! This makes these factors standardised
X BY X1 X2 X3 X4;
M BY M1 M2 M3 M4;
W BY W1* W2 W3 W4;
Z BY Z1* Z2 Z3 Z4;
Y BY Y1 Y2 Y3 Y4;
W@1; Z@1;
! Create latent interactions
MW | M XWITH W;
MZ | M XWITH Z;
XW | X XWITH W;
XZ | X XWITH Z;
WZ | W XWITH Z;
MWZ | M XWITH WZ;
XWZ | X XWITH WZ;
! Fit structural model and name parameters
! Note that intercepts of M, Y are fixed = 0 since they are latent vars
! so no code to state and name them as parameters
Y ON M (b1);
Y ON W (b2);
Y ON Z (b3);
Y ON MW (b4);
Y ON MZ (b5);
Y ON WZ (b6);
Y ON MWZ (b7);
Y ON X(cdash);
M ON X (a1);
M ON W (a2);
M ON Z (a3);
M ON XW (a4);
M ON XZ (a5);
M ON WZ (a6);
M ON XWZ (a7);
! Use model constraint subcommand to test conditional indirect effects
! You need to pick low, medium and high moderator values for W, Z
! for example, of 1 SD below mean, mean, 1 SD above mean
! 2 moderators, 3 values for each, gives 9 combinations
! arbitrary naming convention for conditional indirect and total effects used below:
! MEV_LOQ = medium value of V and low value of Q, etc.
MODEL CONSTRAINT:
NEW(LOW_W MED_W HIGH_W LOW_Z MED_Z HIGH_Z
ILOW_LOZ IMEW_LOZ IHIW_LOZ ILOW_MEZ IMEW_MEZ IHIW_MEZ
ILOW_HIZ IMEW_HIZ IHIW_HIZ
TLOW_LOZ TMEW_LOZ THIW_LOZ TLOW_MEZ TMEW_MEZ THIW_MEZ
TLOW_HIZ TMEW_HIZ THIW_HIZ);
LOW_W = -1;
! -1 SD below mean value of W
MED_W = 0;
! mean value of W
HIGH_W = 1;
! +1 SD above mean value of W
LOW_Z = -1;
! -1 SD below mean value of Z
MED_Z = 0;
! mean value of Z
HIGH_Z = 1;
! +1 SD above mean value of Z
! Calc conditional indirect effects for each combination of moderator values
ILOW_LOZ = a1*b1 + a4*b1*LOW_W + a5*b1*LOW_Z + a7*b1*LOW_W*LOW_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*LOW_Z*LOW_W +
a7*b4*LOW_W*LOW_W*LOW_Z + a1*b5*LOW_Z + a4*b5*LOW_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*LOW_W*LOW_Z*LOW_Z + a1*b7*LOW_W*LOW_Z +
a4*b7*LOW_W*LOW_W*LOW_Z + a5*b7*LOW_W*LOW_Z*LOW_Z +
a7*b7*LOW_W*LOW_W*LOW_Z*LOW_Z;
IMEW_LOZ = a1*b1 + a4*b1*MED_W + a5*b1*LOW_Z + a7*b1*MED_W*LOW_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*LOW_Z*MED_W +
a7*b4*MED_W*MED_W*LOW_Z + a1*b5*LOW_Z + a4*b5*MED_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*MED_W*LOW_Z*LOW_Z + a1*b7*MED_W*LOW_Z +
a4*b7*MED_W*MED_W*LOW_Z + a5*b7*MED_W*LOW_Z*LOW_Z +
a7*b7*MED_W*MED_W*LOW_Z*LOW_Z;
IHIW_LOZ = a1*b1 + a4*b1*HIGH_W + a5*b1*LOW_Z + a7*b1*HIGH_W*LOW_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*LOW_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*LOW_Z + a1*b5*LOW_Z + a4*b5*HIGH_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*HIGH_W*LOW_Z*LOW_Z + a1*b7*HIGH_W*LOW_Z +
a4*b7*HIGH_W*HIGH_W*LOW_Z + a5*b7*HIGH_W*LOW_Z*LOW_Z +
a7*b7*HIGH_W*HIGH_W*LOW_Z*LOW_Z;
ILOW_MEZ = a1*b1 + a4*b1*LOW_W + a5*b1*MED_Z + a7*b1*LOW_W*MED_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*MED_Z*LOW_W +
a7*b4*LOW_W*LOW_W*MED_Z + a1*b5*MED_Z + a4*b5*LOW_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*LOW_W*MED_Z*MED_Z + a1*b7*LOW_W*MED_Z +
a4*b7*LOW_W*LOW_W*MED_Z + a5*b7*LOW_W*MED_Z*MED_Z +
a7*b7*LOW_W*LOW_W*MED_Z*MED_Z;
IMEW_MEZ = a1*b1 + a4*b1*MED_W + a5*b1*MED_Z + a7*b1*MED_W*MED_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*MED_Z*MED_W +
a7*b4*MED_W*MED_W*MED_Z + a1*b5*MED_Z + a4*b5*MED_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*MED_W*MED_Z*MED_Z + a1*b7*MED_W*MED_Z +
a4*b7*MED_W*MED_W*MED_Z + a5*b7*MED_W*MED_Z*MED_Z +
a7*b7*MED_W*MED_W*MED_Z*MED_Z;
IHIW_MEZ = a1*b1 + a4*b1*HIGH_W + a5*b1*MED_Z + a7*b1*HIGH_W*MED_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*MED_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*MED_Z + a1*b5*MED_Z + a4*b5*HIGH_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*HIGH_W*MED_Z*MED_Z + a1*b7*HIGH_W*MED_Z +
a4*b7*HIGH_W*HIGH_W*MED_Z + a5*b7*HIGH_W*MED_Z*MED_Z +
a7*b7*HIGH_W*HIGH_W*MED_Z*MED_Z;
ILOW_HIZ = a1*b1 + a4*b1*LOW_W + a5*b1*HIGH_Z + a7*b1*LOW_W*HIGH_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*HIGH_Z*LOW_W +
a7*b4*LOW_W*LOW_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*LOW_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*LOW_W*HIGH_Z*HIGH_Z + a1*b7*LOW_W*HIGH_Z +
a4*b7*LOW_W*LOW_W*HIGH_Z + a5*b7*LOW_W*HIGH_Z*HIGH_Z +
a7*b7*LOW_W*LOW_W*HIGH_Z*HIGH_Z;
IMEW_HIZ = a1*b1 + a4*b1*MED_W + a5*b1*HIGH_Z + a7*b1*MED_W*HIGH_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*HIGH_Z*MED_W +
a7*b4*MED_W*MED_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*MED_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*MED_W*HIGH_Z*HIGH_Z + a1*b7*MED_W*HIGH_Z +
a4*b7*MED_W*MED_W*HIGH_Z + a5*b7*MED_W*HIGH_Z*HIGH_Z +
a7*b7*MED_W*MED_W*HIGH_Z*HIGH_Z;
IHIW_HIZ = a1*b1 + a4*b1*HIGH_W + a5*b1*HIGH_Z + a7*b1*HIGH_W*HIGH_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*HIGH_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*HIGH_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*HIGH_W*HIGH_Z*HIGH_Z + a1*b7*HIGH_W*HIGH_Z +
a4*b7*HIGH_W*HIGH_W*HIGH_Z + a5*b7*HIGH_W*HIGH_Z*HIGH_Z +
a7*b7*HIGH_W*HIGH_W*HIGH_Z*HIGH_Z;
! Calc conditional total effects for each combination of moderator values
TLOW_LOZ = ILOW_LOZ + cdash;
TMEW_LOZ = IMEW_LOZ + cdash;
THIW_LOZ = IHIW_LOZ + cdash;
TLOW_MEZ = ILOW_MEZ + cdash;
TMEW_MEZ = IMEW_MEZ + cdash;
THIW_MEZ = IHIW_MEZ + cdash;
TLOW_HIZ = ILOW_HIZ + cdash;
TMEW_HIZ = IMEW_HIZ + cdash;
THIW_HIZ = IHIW_HIZ + cdash;代码解读9
USEVARIABLES = X1 X2 X3 X4 M1 M2 M3 M4
W1 W2 W3 W4 Z1 Z2 Z3 Z4
Y1 Y2 Y3 Y4;
ANALYSIS:
TYPE = GENERAL RANDOM;
ESTIMATOR = ML;
ALGORITHM = INTEGRATION;
MODEL:
! Measurement model
! Identify moderator factors by fixing variance = 1 (instead of first loading)
! This makes these factors standardised
X BY X1 X2 X3 X4;
M BY M1 M2 M3 M4;
W BY W1* W2 W3 W4;
Z BY Z1* Z2 Z3 Z4;
Y BY Y1 Y2 Y3 Y4;
W@1; Z@1;
! Create latent interactions
MW | M XWITH W;
MZ | M XWITH Z;
XW | X XWITH W;
XZ | X XWITH Z;
WZ | W XWITH Z;
MWZ | M XWITH WZ;
XWZ | X XWITH WZ;
! Fit structural model and name parameters
! Note that intercepts of M, Y are fixed = 0 since they are latent vars
! so no code to state and name them as parameters
Y ON M (b1);
Y ON W (b2);
Y ON Z (b3);
Y ON MW (b4);
Y ON MZ (b5);
Y ON WZ (b6);
Y ON MWZ (b7);
Y ON X(cdash);
M ON X (a1);
M ON W (a2);
M ON Z (a3);
M ON XW (a4);
M ON XZ (a5);
M ON WZ (a6);
M ON XWZ (a7);
! Use model constraint subcommand to test conditional indirect effects
! You need to pick low, medium and high moderator values for W, Z
! for example, of 1 SD below mean, mean, 1 SD above mean
! 2 moderators, 3 values for each, gives 9 combinations
! arbitrary naming convention for conditional indirect and total effects used below:
! MEV_LOQ = medium value of V and low value of Q, etc.
MODEL CONSTRAINT:
NEW(LOW_W MED_W HIGH_W LOW_Z MED_Z HIGH_Z
ILOW_LOZ IMEW_LOZ IHIW_LOZ ILOW_MEZ IMEW_MEZ IHIW_MEZ
ILOW_HIZ IMEW_HIZ IHIW_HIZ
TLOW_LOZ TMEW_LOZ THIW_LOZ TLOW_MEZ TMEW_MEZ THIW_MEZ
TLOW_HIZ TMEW_HIZ THIW_HIZ);
LOW_W = -1;
! -1 SD below mean value of W
MED_W = 0;
! mean value of W
HIGH_W = 1;
! +1 SD above mean value of W
LOW_Z = -1;
! -1 SD below mean value of Z
MED_Z = 0;
! mean value of Z
HIGH_Z = 1;
! +1 SD above mean value of Z
! Calc conditional indirect effects for each combination of moderator values
ILOW_LOZ = a1*b1 + a4*b1*LOW_W + a5*b1*LOW_Z + a7*b1*LOW_W*LOW_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*LOW_Z*LOW_W +
a7*b4*LOW_W*LOW_W*LOW_Z + a1*b5*LOW_Z + a4*b5*LOW_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*LOW_W*LOW_Z*LOW_Z + a1*b7*LOW_W*LOW_Z +
a4*b7*LOW_W*LOW_W*LOW_Z + a5*b7*LOW_W*LOW_Z*LOW_Z +
a7*b7*LOW_W*LOW_W*LOW_Z*LOW_Z;
IMEW_LOZ = a1*b1 + a4*b1*MED_W + a5*b1*LOW_Z + a7*b1*MED_W*LOW_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*LOW_Z*MED_W +
a7*b4*MED_W*MED_W*LOW_Z + a1*b5*LOW_Z + a4*b5*MED_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*MED_W*LOW_Z*LOW_Z + a1*b7*MED_W*LOW_Z +
a4*b7*MED_W*MED_W*LOW_Z + a5*b7*MED_W*LOW_Z*LOW_Z +
a7*b7*MED_W*MED_W*LOW_Z*LOW_Z;
IHIW_LOZ = a1*b1 + a4*b1*HIGH_W + a5*b1*LOW_Z + a7*b1*HIGH_W*LOW_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*LOW_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*LOW_Z + a1*b5*LOW_Z + a4*b5*HIGH_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*HIGH_W*LOW_Z*LOW_Z + a1*b7*HIGH_W*LOW_Z +
a4*b7*HIGH_W*HIGH_W*LOW_Z + a5*b7*HIGH_W*LOW_Z*LOW_Z +
a7*b7*HIGH_W*HIGH_W*LOW_Z*LOW_Z;
ILOW_MEZ = a1*b1 + a4*b1*LOW_W + a5*b1*MED_Z + a7*b1*LOW_W*MED_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*MED_Z*LOW_W +
a7*b4*LOW_W*LOW_W*MED_Z + a1*b5*MED_Z + a4*b5*LOW_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*LOW_W*MED_Z*MED_Z + a1*b7*LOW_W*MED_Z +
a4*b7*LOW_W*LOW_W*MED_Z + a5*b7*LOW_W*MED_Z*MED_Z +
a7*b7*LOW_W*LOW_W*MED_Z*MED_Z;
IMEW_MEZ = a1*b1 + a4*b1*MED_W + a5*b1*MED_Z + a7*b1*MED_W*MED_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*MED_Z*MED_W +
a7*b4*MED_W*MED_W*MED_Z + a1*b5*MED_Z + a4*b5*MED_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*MED_W*MED_Z*MED_Z + a1*b7*MED_W*MED_Z +
a4*b7*MED_W*MED_W*MED_Z + a5*b7*MED_W*MED_Z*MED_Z +
a7*b7*MED_W*MED_W*MED_Z*MED_Z;
IHIW_MEZ = a1*b1 + a4*b1*HIGH_W + a5*b1*MED_Z + a7*b1*HIGH_W*MED_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*MED_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*MED_Z + a1*b5*MED_Z + a4*b5*HIGH_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*HIGH_W*MED_Z*MED_Z + a1*b7*HIGH_W*MED_Z +
a4*b7*HIGH_W*HIGH_W*MED_Z + a5*b7*HIGH_W*MED_Z*MED_Z +
a7*b7*HIGH_W*HIGH_W*MED_Z*MED_Z;
ILOW_HIZ = a1*b1 + a4*b1*LOW_W + a5*b1*HIGH_Z + a7*b1*LOW_W*HIGH_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*HIGH_Z*LOW_W +
a7*b4*LOW_W*LOW_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*LOW_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*LOW_W*HIGH_Z*HIGH_Z + a1*b7*LOW_W*HIGH_Z +
a4*b7*LOW_W*LOW_W*HIGH_Z + a5*b7*LOW_W*HIGH_Z*HIGH_Z +
a7*b7*LOW_W*LOW_W*HIGH_Z*HIGH_Z;
IMEW_HIZ = a1*b1 + a4*b1*MED_W + a5*b1*HIGH_Z + a7*b1*MED_W*HIGH_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*HIGH_Z*MED_W +
a7*b4*MED_W*MED_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*MED_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*MED_W*HIGH_Z*HIGH_Z + a1*b7*MED_W*HIGH_Z +
a4*b7*MED_W*MED_W*HIGH_Z + a5*b7*MED_W*HIGH_Z*HIGH_Z +
a7*b7*MED_W*MED_W*HIGH_Z*HIGH_Z;
IHIW_HIZ = a1*b1 + a4*b1*HIGH_W + a5*b1*HIGH_Z + a7*b1*HIGH_W*HIGH_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*HIGH_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*HIGH_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*HIGH_W*HIGH_Z*HIGH_Z + a1*b7*HIGH_W*HIGH_Z +
a4*b7*HIGH_W*HIGH_W*HIGH_Z + a5*b7*HIGH_W*HIGH_Z*HIGH_Z +
a7*b7*HIGH_W*HIGH_W*HIGH_Z*HIGH_Z;
! Calc conditional total effects for each combination of moderator values
TLOW_LOZ = ILOW_LOZ + cdash;
TMEW_LOZ = IMEW_LOZ + cdash;
THIW_LOZ = IHIW_LOZ + cdash;
TLOW_MEZ = ILOW_MEZ + cdash;
TMEW_MEZ = IMEW_MEZ + cdash;
THIW_MEZ = IHIW_MEZ + cdash;
TLOW_HIZ = ILOW_HIZ + cdash;
TMEW_HIZ = IMEW_HIZ + cdash;
THIW_HIZ = IHIW_HIZ + cdash;
! Use loop plot to plot conditional indirect effect of X on Y for each combination of low, med, high moderator values
! Could be edited to show conditional direct or conditional total effects instead
! NOTE - values from -3 to 3 in LOOP() statement since
! X is factor with mean set at default of 0
PLOT(PLOW_LOZ PMEW_LOZ PHIW_LOZ PLOW_MEZ PMEW_MEZ PHIW_MEZ
PLOW_HIZ PMEW_HIZ PHIW_HIZ);
LOOP(XVAL,-3,3,0.1);
PLOW_LOZ = ILOW_LOZ*XVAL;
PMEW_LOZ = IMEW_LOZ*XVAL;
PHIW_LOZ = IHIW_LOZ*XVAL;
PLOW_MEZ = ILOW_MEZ*XVAL;
PMEW_MEZ = IMEW_MEZ*XVAL;
PHIW_MEZ = IHIW_MEZ*XVAL;
PLOW_HIZ = ILOW_HIZ*XVAL;
PMEW_HIZ = IMEW_HIZ*XVAL;
PHIW_HIZ = IHIW_HIZ*XVAL;代码解读10
USEVARIABLES = X1 X2 X3 X4 M1 M2 M3 M4
W1 W2 W3 W4 Z1 Z2 Z3 Z4
Y1 Y2 Y3 Y4;
ANALYSIS:
TYPE = GENERAL RANDOM;
ESTIMATOR = ML;
ALGORITHM = INTEGRATION;
MODEL:
! Measurement model
! Identify moderator factors by fixing variance = 1 (instead of first loading)
! This makes these factors standardised
X BY X1 X2 X3 X4;
M BY M1 M2 M3 M4;
W BY W1* W2 W3 W4;
Z BY Z1* Z2 Z3 Z4;
Y BY Y1 Y2 Y3 Y4;
W@1; Z@1;
! Create latent interactions
MW | M XWITH W;
MZ | M XWITH Z;
XW | X XWITH W;
XZ | X XWITH Z;
WZ | W XWITH Z;
MWZ | M XWITH WZ;
XWZ | X XWITH WZ;
! Fit structural model and name parameters
! Note that intercepts of M, Y are fixed = 0 since they are latent vars
! so no code to state and name them as parameters
Y ON M (b1);
Y ON W (b2);
Y ON Z (b3);
Y ON MW (b4);
Y ON MZ (b5);
Y ON WZ (b6);
Y ON MWZ (b7);
Y ON X(cdash);
M ON X (a1);
M ON W (a2);
M ON Z (a3);
M ON XW (a4);
M ON XZ (a5);
M ON WZ (a6);
M ON XWZ (a7);
! Use model constraint subcommand to test conditional indirect effects
! You need to pick low, medium and high moderator values for W, Z
! for example, of 1 SD below mean, mean, 1 SD above mean
! 2 moderators, 3 values for each, gives 9 combinations
! arbitrary naming convention for conditional indirect and total effects used below:
! MEV_LOQ = medium value of V and low value of Q, etc.
MODEL CONSTRAINT:
NEW(LOW_W MED_W HIGH_W LOW_Z MED_Z HIGH_Z
ILOW_LOZ IMEW_LOZ IHIW_LOZ ILOW_MEZ IMEW_MEZ IHIW_MEZ
ILOW_HIZ IMEW_HIZ IHIW_HIZ
TLOW_LOZ TMEW_LOZ THIW_LOZ TLOW_MEZ TMEW_MEZ THIW_MEZ
TLOW_HIZ TMEW_HIZ THIW_HIZ);
LOW_W = -1;
! -1 SD below mean value of W
MED_W = 0;
! mean value of W
HIGH_W = 1;
! +1 SD above mean value of W
LOW_Z = -1;
! -1 SD below mean value of Z
MED_Z = 0;
! mean value of Z
HIGH_Z = 1;
! +1 SD above mean value of Z
! Calc conditional indirect effects for each combination of moderator values
ILOW_LOZ = a1*b1 + a4*b1*LOW_W + a5*b1*LOW_Z + a7*b1*LOW_W*LOW_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*LOW_Z*LOW_W +
a7*b4*LOW_W*LOW_W*LOW_Z + a1*b5*LOW_Z + a4*b5*LOW_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*LOW_W*LOW_Z*LOW_Z + a1*b7*LOW_W*LOW_Z +
a4*b7*LOW_W*LOW_W*LOW_Z + a5*b7*LOW_W*LOW_Z*LOW_Z +
a7*b7*LOW_W*LOW_W*LOW_Z*LOW_Z;
IMEW_LOZ = a1*b1 + a4*b1*MED_W + a5*b1*LOW_Z + a7*b1*MED_W*LOW_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*LOW_Z*MED_W +
a7*b4*MED_W*MED_W*LOW_Z + a1*b5*LOW_Z + a4*b5*MED_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*MED_W*LOW_Z*LOW_Z + a1*b7*MED_W*LOW_Z +
a4*b7*MED_W*MED_W*LOW_Z + a5*b7*MED_W*LOW_Z*LOW_Z +
a7*b7*MED_W*MED_W*LOW_Z*LOW_Z;
IHIW_LOZ = a1*b1 + a4*b1*HIGH_W + a5*b1*LOW_Z + a7*b1*HIGH_W*LOW_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*LOW_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*LOW_Z + a1*b5*LOW_Z + a4*b5*HIGH_W*LOW_Z +
a5*b5*LOW_Z*LOW_Z + a7*b5*HIGH_W*LOW_Z*LOW_Z + a1*b7*HIGH_W*LOW_Z +
a4*b7*HIGH_W*HIGH_W*LOW_Z + a5*b7*HIGH_W*LOW_Z*LOW_Z +
a7*b7*HIGH_W*HIGH_W*LOW_Z*LOW_Z;
ILOW_MEZ = a1*b1 + a4*b1*LOW_W + a5*b1*MED_Z + a7*b1*LOW_W*MED_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*MED_Z*LOW_W +
a7*b4*LOW_W*LOW_W*MED_Z + a1*b5*MED_Z + a4*b5*LOW_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*LOW_W*MED_Z*MED_Z + a1*b7*LOW_W*MED_Z +
a4*b7*LOW_W*LOW_W*MED_Z + a5*b7*LOW_W*MED_Z*MED_Z +
a7*b7*LOW_W*LOW_W*MED_Z*MED_Z;
IMEW_MEZ = a1*b1 + a4*b1*MED_W + a5*b1*MED_Z + a7*b1*MED_W*MED_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*MED_Z*MED_W +
a7*b4*MED_W*MED_W*MED_Z + a1*b5*MED_Z + a4*b5*MED_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*MED_W*MED_Z*MED_Z + a1*b7*MED_W*MED_Z +
a4*b7*MED_W*MED_W*MED_Z + a5*b7*MED_W*MED_Z*MED_Z +
a7*b7*MED_W*MED_W*MED_Z*MED_Z;
IHIW_MEZ = a1*b1 + a4*b1*HIGH_W + a5*b1*MED_Z + a7*b1*HIGH_W*MED_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*MED_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*MED_Z + a1*b5*MED_Z + a4*b5*HIGH_W*MED_Z +
a5*b5*MED_Z*MED_Z + a7*b5*HIGH_W*MED_Z*MED_Z + a1*b7*HIGH_W*MED_Z +
a4*b7*HIGH_W*HIGH_W*MED_Z + a5*b7*HIGH_W*MED_Z*MED_Z +
a7*b7*HIGH_W*HIGH_W*MED_Z*MED_Z;
ILOW_HIZ = a1*b1 + a4*b1*LOW_W + a5*b1*HIGH_Z + a7*b1*LOW_W*HIGH_Z +
a1*b4*LOW_W + a4*b4*LOW_W*LOW_W + a5*b4*HIGH_Z*LOW_W +
a7*b4*LOW_W*LOW_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*LOW_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*LOW_W*HIGH_Z*HIGH_Z + a1*b7*LOW_W*HIGH_Z +
a4*b7*LOW_W*LOW_W*HIGH_Z + a5*b7*LOW_W*HIGH_Z*HIGH_Z +
a7*b7*LOW_W*LOW_W*HIGH_Z*HIGH_Z;
IMEW_HIZ = a1*b1 + a4*b1*MED_W + a5*b1*HIGH_Z + a7*b1*MED_W*HIGH_Z +
a1*b4*MED_W + a4*b4*MED_W*MED_W + a5*b4*HIGH_Z*MED_W +
a7*b4*MED_W*MED_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*MED_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*MED_W*HIGH_Z*HIGH_Z + a1*b7*MED_W*HIGH_Z +
a4*b7*MED_W*MED_W*HIGH_Z + a5*b7*MED_W*HIGH_Z*HIGH_Z +
a7*b7*MED_W*MED_W*HIGH_Z*HIGH_Z;
IHIW_HIZ = a1*b1 + a4*b1*HIGH_W + a5*b1*HIGH_Z + a7*b1*HIGH_W*HIGH_Z +
a1*b4*HIGH_W + a4*b4*HIGH_W*HIGH_W + a5*b4*HIGH_Z*HIGH_W +
a7*b4*HIGH_W*HIGH_W*HIGH_Z + a1*b5*HIGH_Z + a4*b5*HIGH_W*HIGH_Z +
a5*b5*HIGH_Z*HIGH_Z + a7*b5*HIGH_W*HIGH_Z*HIGH_Z + a1*b7*HIGH_W*HIGH_Z +
a4*b7*HIGH_W*HIGH_W*HIGH_Z + a5*b7*HIGH_W*HIGH_Z*HIGH_Z +
a7*b7*HIGH_W*HIGH_W*HIGH_Z*HIGH_Z;
! Calc conditional total effects for each combination of moderator values
TLOW_LOZ = ILOW_LOZ + cdash;
TMEW_LOZ = IMEW_LOZ + cdash;
THIW_LOZ = IHIW_LOZ + cdash;
TLOW_MEZ = ILOW_MEZ + cdash;
TMEW_MEZ = IMEW_MEZ + cdash;
THIW_MEZ = IHIW_MEZ + cdash;
TLOW_HIZ = ILOW_HIZ + cdash;
TMEW_HIZ = IMEW_HIZ + cdash;
THIW_HIZ = IHIW_HIZ + cdash;
! Use loop plot to plot conditional indirect effect of X on Y for each combination of low, med, high moderator values
! Could be edited to show conditional direct or conditional total effects instead
! NOTE - values from -3 to 3 in LOOP() statement since
! X is factor with mean set at default of 0
PLOT(PLOW_LOZ PMEW_LOZ PHIW_LOZ PLOW_MEZ PMEW_MEZ PHIW_MEZ
PLOW_HIZ PMEW_HIZ PHIW_HIZ);
LOOP(XVAL,-3,3,0.1);
PLOW_LOZ = ILOW_LOZ*XVAL;
PMEW_LOZ = IMEW_LOZ*XVAL;
PHIW_LOZ = IHIW_LOZ*XVAL;
PLOW_MEZ = ILOW_MEZ*XVAL;
PMEW_MEZ = IMEW_MEZ*XVAL;
PHIW_MEZ = IHIW_MEZ*XVAL;
PLOW_HIZ = ILOW_HIZ*XVAL;
PMEW_HIZ = IMEW_HIZ*XVAL;
PHIW_HIZ = IHIW_HIZ*XVAL;
PLOT:
TYPE = plot2;
OUTPUT:
CINT;